18.2.1 矩形复习课 课件(31张PPT)
文档属性
| 名称 | 18.2.1 矩形复习课 课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 656.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 16:44:24 | ||
图片预览








文档简介
(共31张PPT)
《平行四边形》18.2.1
矩形 复习课
复习目标:
1.进一步加深对矩形性质与判定定理的理解,提高对矩形知识的综合运用能力
2.熟练应用矩形的性质和判定进行有关证明和计算
边 角 矩形对边平行且相等
矩形的四个角都是直角
对角线 矩形的对角线相等且互相平分
矩形的性质
对称性 是轴对称图形,有两条对称轴
有一个角是直角的平行四边形叫做矩形
矩形定义
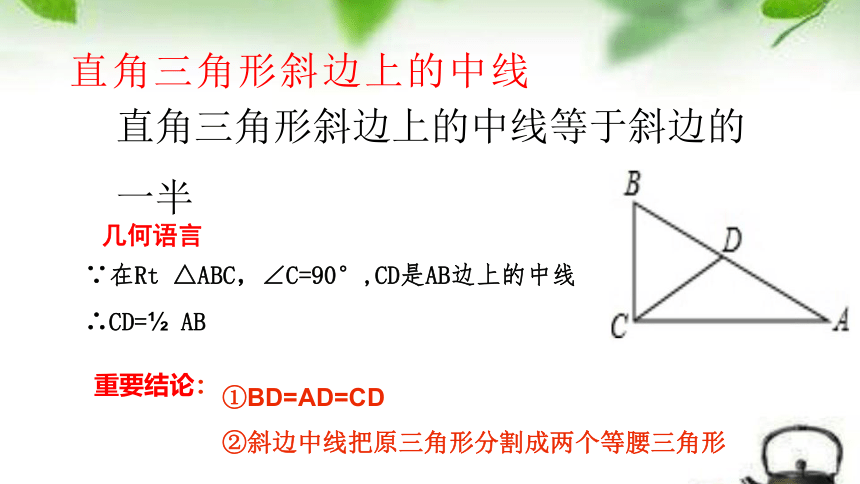
直角三角形斜边上的中线
直角三角形斜边上的中线等于斜边的一半
几何语言
重要结论:
①BD=AD=CD
②斜边中线把原三角形分割成两个等腰三角形
∵在Rt △ABC,∠C=90°,CD是AB边上的中线
∴CD= AB
矩形的判定
判定1 有一个角是直角的平行四边形是矩形
(定义法)
判定2 有三个角是直角的四边形是矩形
判定3 对角线相等的平行四边形是矩形
题型一 矩形的性质
1.矩形具有而平行四边形不一定具有的性质是 (填代号)_________
①对边平行且相等;
②对角线互相平分;
③对角相等;
④对角线相等;
⑤4个角都是90°;
⑥轴对称图形
④
⑤
⑥
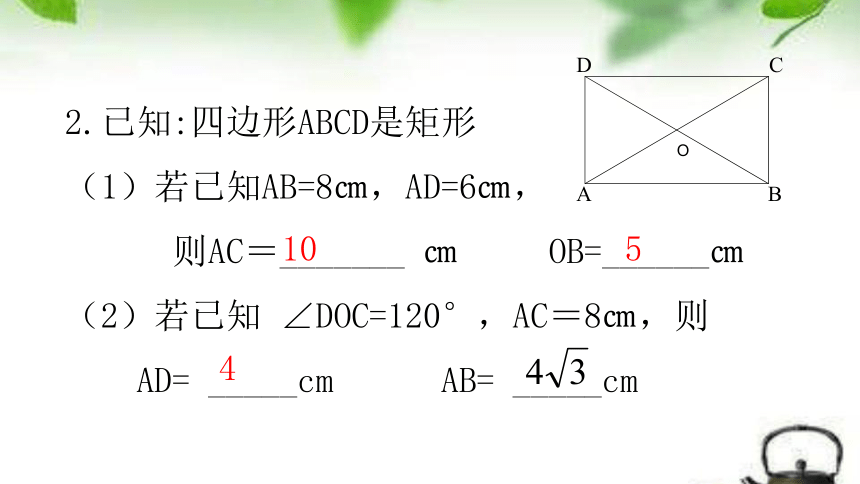
2.已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=______㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则
AD= _____cm AB= _____cm
D C
A B
O
10
5
4
3 .如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ AC、BD是矩形ABCD的对角线
∴ AC=BD=13cm(矩形的对角线相等)
∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
A D
B C
O
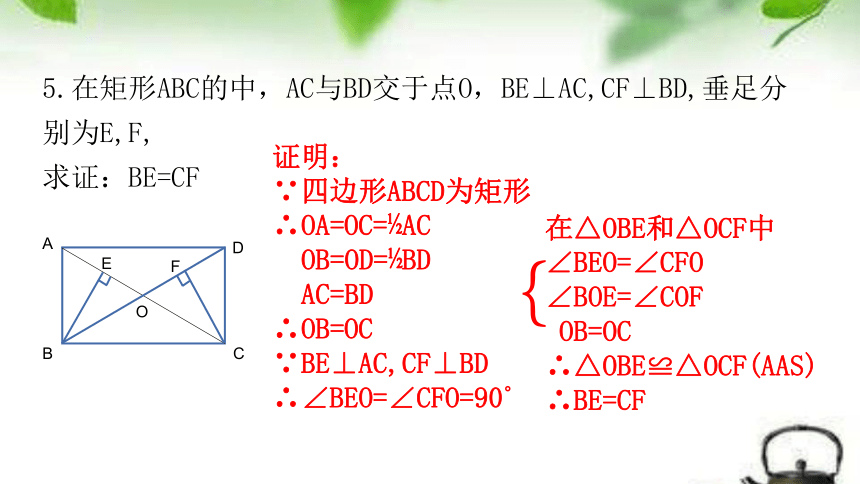
5.在矩形ABC的中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F,
求证:BE=CF
A
D
C
B
E
F
O
证明:
∵四边形ABCD为矩形
∴OA=OC= AC
OB=OD= BD
AC=BD
∴OB=OC
∵BE⊥AC,CF⊥BD
∴∠BEO=∠CFO=90
在△OBE和△OCF中
∠BEO=∠CFO
∠BOE=∠COF
OB=OC
∴△OBE≌△OCF(AAS)
∴BE=CF
{
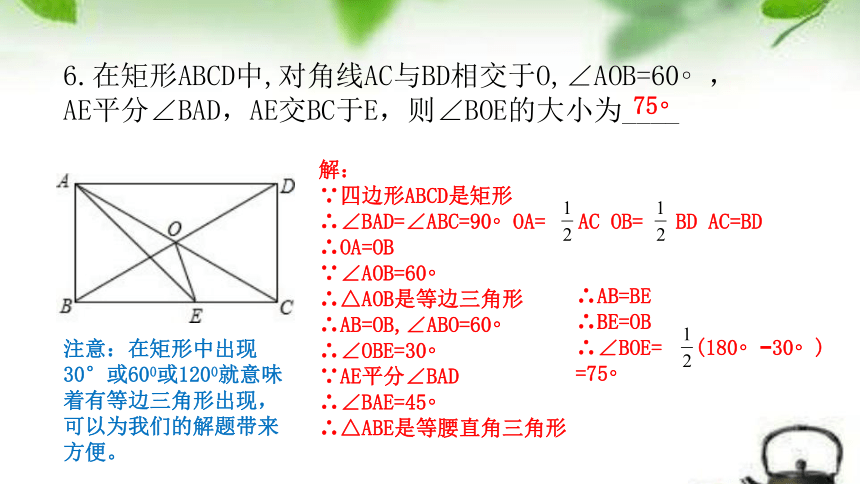
解:
∵四边形ABCD是矩形
∴∠BAD=∠ABC=90 OA= AC OB= BD AC=BD
∴OA=OB
∵∠AOB=60
∴△AOB是等边三角形
∴AB=OB,∠ABO=60
∴∠OBE=30
∵AE平分∠BAD
∴∠BAE=45
∴△ABE是等腰直角三角形
∴AB=BE
∴BE=OB
∴∠BOE= (180 30 ) =75
6.在矩形ABCD中,对角线AC与BD相交于O,∠AOB=60 ,AE平分∠BAD,AE交BC于E,则∠BOE的大小为____
75
注意:在矩形中出现30°或600或1200就意味着有等边三角形出现,
可以为我们的解题带来方便。
7.如图所示,将矩形ABCD沿对角线BD折叠,点BC'与AD交于点E,若AD=8cm,AB=4cm,求△BDE的面积
解:设DE=xcm,则AE=(8-x)cm
由折叠的性质知△BCD与△BC D全等,
则∠1=∠2.
在矩形ABCD中,∵AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴BE=DE=xcm.
在Rt△ABE中,由勾股定理,
得B =A + A ,
即 = + ,
解得x=5
∴△BDE的面积为= DE·AB=
x5x4=10(cm2)
点拨:
解决矩形折叠问题的方法
1利用折叠的性质:折叠前
后的图形能够完全重合,
折叠前后的图形对应边相
等,对应角相等
2.此类问题往往通过图形
间的折叠找出折叠部分与
原图形中线段或角的关
系,从而得到折叠部分与
原图形或其他图形中线段
或角的关系
题型二 直角三角形斜边上的中线性质
1.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A. 下滑时,OP增大
B. 上升时,OP减小
C. 无论怎样滑动,OP不变
D. 只要滑动,OP就变化
解析:
∵AO⊥BO,点P是AB中点
∴OP= AB,
∴在滑动的过程中OP的长度不变。
故选:C
C
2.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,求四边形ABOM的周长。
解:
∵矩形ABCD中,AB=5,AD=12,
∴BC=AD=12,CD=AB=5,∠ABC=90 ,OA=OC=OB,
∴AC= =13,
∴OB = OA = OC = AC = 6.5,
∵M是AD的中点,O是AC中点
∴OM= CD=2.5, AM= AD=6,
∴四边形ABOM的周长为:AB+OB+OM+AM=5+6.5+2.5+6=20.
3.BD,CE是△ABC的两条高,M,N分别是BC,DE的中点。
求证:MN⊥DE
证明:
连接EM,DM
∵BD,CE为△ABC的两条高,
∴BD⊥AC,CE⊥AB,
∴∠BEC=∠CDB=90°
在Rt△BEC中,
∵M为斜边BC的中点,
∴EM= BC
在Rt△CDB中,
∵M为斜边BC的中点,
∴DM= BC.
∴EM=DM
△EMD是等腰三角形
又∵N为DE的中点,
∴MN⊥DE.
点拨:在直角三角形中,遇到斜边的中点常作斜边上的中线,从而利用直角三角形斜边上的中线的性质把问题化为等腰三角形的问题,利用等腰三角形的性质解决。
4.如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
(1)若EF=3,BC=8,求△EFM的周长
(2)若∠ABC=28 ,∠ACB=48 ,求△EFM的三个内角的度数。
∟
∟
(1)解:
∵CE⊥BA,M为BC的中点,
∴EM= BC=4,
∵BF⊥CA,M为BC的中点,
∴FM= BC=4,
∴△EFM的周长为:EM+FM+EF=4+4+3=11.
∟
∟
(2)解:
∵EM= BC,M为BC的中点,∴BM= BC
∴BM=EM,
∴∠ABC=∠BEM=28 ,
∴∠EMC=56 ,
∵FM= BC,M为BC的中点,∴CM= BC
∴FM=MC,
∴∠MFC=∠ACB=48 ,
∴∠FMC=84 ,
∴∠FME=84 56 =28 ,
∵FM=EM=4,
∴∠MEF=∠MFE,
∴∠FEM=∠EFM=76
题型三 矩形的判定
A
B
C
D
E
1.点E是 ABCD的边AB的中点,且EC=ED.
求证:四边形ABCD是矩形
证明:
∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC
∵E是边AB的中点
∴AE=BE
∵ED=EC
∴△AED≌△BEC,∴∠A=∠B.
∵AD∥BC ∴∠A+∠B=180°,
∴∠A=∠B=90° ∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
2.已知:如图,在 ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足。
(1)求证:△ABE≌△CDF
(2)求证:四边形AECF是矩形
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D AB=CD AD∥BC
∵AE⊥BC CF⊥AD
∴∠AEB=∠AEC=∠CFD=∠AFC=90°
∠AEB=∠CFD
在△ABE和△CDF中 ∠B=∠D
AB=CD,
∴△ABE≌△CDF(AAS)
{
(2)∵AD∥BC
∴∠EAF=∠AEB=90°,
∴∠EAF=∠AEC=∠AFC=90°∴四边形AECF是矩形(有三
个角是直角的四边形是矩形)
3.在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC
的平行线交BE的延长线于点F,且AF=CD,连接CF
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论
解:(1)证明:
∵E是AD的中点
∴AE=DE
∵AF∥BC
∴∠AFE=∠DBE
∠EAF=∠EDB
∴△AEF≌△DEB
(2)四边形ADCF是矩形
证明:
∵AF∥CD,且AF=CD,
∴四边形ADCF是平行四边形
∵△AEF≌△DEB∴AF=BD
∴BD=CD,即AD是△ABC的中线
∵AB=AC ∴AD⊥BC ∴∠ADC=90°
∴ 四边形ADCF是矩形(定义法)
4.如图,△BDE中,BD=DE, C为BE中点, 四边形ACED是平行四边形.
求证:四边形ABCD是矩形.
证明:∵ C为BE的中点
∴BC=CE
∵四边形ACED是平行四边形
∴AC=DE AD∥CE且AD=CE
∴AD∥BC且AD=BC
∴四边形ABCD是平行四边形
∵AC=DE
又BD=DE
∴BD=AC
∴平行四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
1.在矩形ABCD中,M是CD的中点,P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的值可能是( )
A 3.2 B 3.5 C 3.6 D 3.8
解析:∵AP+PB=AB
∴PM最小时,PA+PB+PM的值是最小值,
由垂线段最短可知PM⊥CD时,PA+PB+PM的值是最小值,
最小值为1+2=3.当P在B点时PA+PB+PM=AB+BM=2+√2
≈ 3.4
∴PA+PB+PM的值范围为3≤PA+PB+PM<3.4,故选:A.
A
题型四 矩形中的动点问题
2.如图,在矩形ABCD中,AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,如果点P、Q分别从A. C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒。
(1)当t=2秒时,求P、Q两点之间的距离;
(2)t为何值时,线段AQ与DP互相平分
(3)t为何值时,四边形APQD的面积为矩形面积的
(1)如图所示:连接PQ,过点P作PE⊥DQ于点E,则DE=AP,PE=BC
∵AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,
∴当t=2秒时,QC=4cm,AP=8cm,
∴DQ=24 QC=20,则EQ=12,
∴PQ= = = (cm)
(2)∵AP=4t,DQ=24 2t,
当线段AQ与DP互相平分,则四边形APQD为矩形时,
则AP=DQ,即4t=24 2t,
解得:t=4.
故t为4秒时,线段AQ与DP互相平分
(3)∵P在AB上,
∴SAPQD= (DQ+AP)·AD,= (4t+24 2t)×10,=(10t+120)(cm2)(0S矩形ABCD=10×24=240,
∴10t+120= ×240,
解得:t=3.
∴t为3秒时,四边形APQD的面积为矩形面积的 .
当堂检测
1.如图(左),在Rt△ABC中,∠ACB=90 ,D. E. F分别是AB、BC、CA的中点,若CD=5cm,则EF=___cm.
5
2.如图(右),Rt△ABC中,斜边BC上的高线AD=5cm,斜边BC上的中线AE=6cm,则△ABC的面积为______cm2.
30
3.如图(左),在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A. B.2 C. D.1
A
4.如图(右),△ABC是以AB为斜边的直角三角形,AC= 4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值为 .
2.4
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.
(1)求∠AOB的度数;
(2)若AB=2 cm,求矩形ABCD的面积.
解:(1)∵四边形ABCD是矩形,
∴AC=BD,∴BO=AO,∴∠OBA=∠OAB.
又∵AE⊥BD,且AE平分∠BAO,
∴∠BAE=1/2∠OAB,∠BAE+∠OBA=90°.
∴∠OBA=60°,
∴△AOB是等边三角形,
∴∠AOB=60°.
(2)∵△AOB是等边三角形,四边形ABCD是矩形
∴∠BAO=60°,∠ABC=90°∴∠ACB=30°.
∴AC=2AB=4 cm,BC= =2 cm.
∴S矩形ABCD=2×2 =4 (cm2).
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
证明:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,AC=BD
∵OD= BD,OC= AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO,
在△ODE与△OCF中,
DE=CF ∠EDO=∠FCO OD=OC,
∴△ODE≌△OCF(SAS),
∴OE=OF.
再 见
《平行四边形》18.2.1
矩形 复习课
复习目标:
1.进一步加深对矩形性质与判定定理的理解,提高对矩形知识的综合运用能力
2.熟练应用矩形的性质和判定进行有关证明和计算
边 角 矩形对边平行且相等
矩形的四个角都是直角
对角线 矩形的对角线相等且互相平分
矩形的性质
对称性 是轴对称图形,有两条对称轴
有一个角是直角的平行四边形叫做矩形
矩形定义
直角三角形斜边上的中线
直角三角形斜边上的中线等于斜边的一半
几何语言
重要结论:
①BD=AD=CD
②斜边中线把原三角形分割成两个等腰三角形
∵在Rt △ABC,∠C=90°,CD是AB边上的中线
∴CD= AB
矩形的判定
判定1 有一个角是直角的平行四边形是矩形
(定义法)
判定2 有三个角是直角的四边形是矩形
判定3 对角线相等的平行四边形是矩形
题型一 矩形的性质
1.矩形具有而平行四边形不一定具有的性质是 (填代号)_________
①对边平行且相等;
②对角线互相平分;
③对角相等;
④对角线相等;
⑤4个角都是90°;
⑥轴对称图形
④
⑤
⑥
2.已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=______㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则
AD= _____cm AB= _____cm
D C
A B
O
10
5
4
3 .如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ AC、BD是矩形ABCD的对角线
∴ AC=BD=13cm(矩形的对角线相等)
∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
A D
B C
O
5.在矩形ABC的中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F,
求证:BE=CF
A
D
C
B
E
F
O
证明:
∵四边形ABCD为矩形
∴OA=OC= AC
OB=OD= BD
AC=BD
∴OB=OC
∵BE⊥AC,CF⊥BD
∴∠BEO=∠CFO=90
在△OBE和△OCF中
∠BEO=∠CFO
∠BOE=∠COF
OB=OC
∴△OBE≌△OCF(AAS)
∴BE=CF
{
解:
∵四边形ABCD是矩形
∴∠BAD=∠ABC=90 OA= AC OB= BD AC=BD
∴OA=OB
∵∠AOB=60
∴△AOB是等边三角形
∴AB=OB,∠ABO=60
∴∠OBE=30
∵AE平分∠BAD
∴∠BAE=45
∴△ABE是等腰直角三角形
∴AB=BE
∴BE=OB
∴∠BOE= (180 30 ) =75
6.在矩形ABCD中,对角线AC与BD相交于O,∠AOB=60 ,AE平分∠BAD,AE交BC于E,则∠BOE的大小为____
75
注意:在矩形中出现30°或600或1200就意味着有等边三角形出现,
可以为我们的解题带来方便。
7.如图所示,将矩形ABCD沿对角线BD折叠,点BC'与AD交于点E,若AD=8cm,AB=4cm,求△BDE的面积
解:设DE=xcm,则AE=(8-x)cm
由折叠的性质知△BCD与△BC D全等,
则∠1=∠2.
在矩形ABCD中,∵AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴BE=DE=xcm.
在Rt△ABE中,由勾股定理,
得B =A + A ,
即 = + ,
解得x=5
∴△BDE的面积为= DE·AB=
x5x4=10(cm2)
点拨:
解决矩形折叠问题的方法
1利用折叠的性质:折叠前
后的图形能够完全重合,
折叠前后的图形对应边相
等,对应角相等
2.此类问题往往通过图形
间的折叠找出折叠部分与
原图形中线段或角的关
系,从而得到折叠部分与
原图形或其他图形中线段
或角的关系
题型二 直角三角形斜边上的中线性质
1.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A. 下滑时,OP增大
B. 上升时,OP减小
C. 无论怎样滑动,OP不变
D. 只要滑动,OP就变化
解析:
∵AO⊥BO,点P是AB中点
∴OP= AB,
∴在滑动的过程中OP的长度不变。
故选:C
C
2.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,求四边形ABOM的周长。
解:
∵矩形ABCD中,AB=5,AD=12,
∴BC=AD=12,CD=AB=5,∠ABC=90 ,OA=OC=OB,
∴AC= =13,
∴OB = OA = OC = AC = 6.5,
∵M是AD的中点,O是AC中点
∴OM= CD=2.5, AM= AD=6,
∴四边形ABOM的周长为:AB+OB+OM+AM=5+6.5+2.5+6=20.
3.BD,CE是△ABC的两条高,M,N分别是BC,DE的中点。
求证:MN⊥DE
证明:
连接EM,DM
∵BD,CE为△ABC的两条高,
∴BD⊥AC,CE⊥AB,
∴∠BEC=∠CDB=90°
在Rt△BEC中,
∵M为斜边BC的中点,
∴EM= BC
在Rt△CDB中,
∵M为斜边BC的中点,
∴DM= BC.
∴EM=DM
△EMD是等腰三角形
又∵N为DE的中点,
∴MN⊥DE.
点拨:在直角三角形中,遇到斜边的中点常作斜边上的中线,从而利用直角三角形斜边上的中线的性质把问题化为等腰三角形的问题,利用等腰三角形的性质解决。
4.如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
(1)若EF=3,BC=8,求△EFM的周长
(2)若∠ABC=28 ,∠ACB=48 ,求△EFM的三个内角的度数。
∟
∟
(1)解:
∵CE⊥BA,M为BC的中点,
∴EM= BC=4,
∵BF⊥CA,M为BC的中点,
∴FM= BC=4,
∴△EFM的周长为:EM+FM+EF=4+4+3=11.
∟
∟
(2)解:
∵EM= BC,M为BC的中点,∴BM= BC
∴BM=EM,
∴∠ABC=∠BEM=28 ,
∴∠EMC=56 ,
∵FM= BC,M为BC的中点,∴CM= BC
∴FM=MC,
∴∠MFC=∠ACB=48 ,
∴∠FMC=84 ,
∴∠FME=84 56 =28 ,
∵FM=EM=4,
∴∠MEF=∠MFE,
∴∠FEM=∠EFM=76
题型三 矩形的判定
A
B
C
D
E
1.点E是 ABCD的边AB的中点,且EC=ED.
求证:四边形ABCD是矩形
证明:
∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC
∵E是边AB的中点
∴AE=BE
∵ED=EC
∴△AED≌△BEC,∴∠A=∠B.
∵AD∥BC ∴∠A+∠B=180°,
∴∠A=∠B=90° ∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
2.已知:如图,在 ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足。
(1)求证:△ABE≌△CDF
(2)求证:四边形AECF是矩形
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D AB=CD AD∥BC
∵AE⊥BC CF⊥AD
∴∠AEB=∠AEC=∠CFD=∠AFC=90°
∠AEB=∠CFD
在△ABE和△CDF中 ∠B=∠D
AB=CD,
∴△ABE≌△CDF(AAS)
{
(2)∵AD∥BC
∴∠EAF=∠AEB=90°,
∴∠EAF=∠AEC=∠AFC=90°∴四边形AECF是矩形(有三
个角是直角的四边形是矩形)
3.在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC
的平行线交BE的延长线于点F,且AF=CD,连接CF
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论
解:(1)证明:
∵E是AD的中点
∴AE=DE
∵AF∥BC
∴∠AFE=∠DBE
∠EAF=∠EDB
∴△AEF≌△DEB
(2)四边形ADCF是矩形
证明:
∵AF∥CD,且AF=CD,
∴四边形ADCF是平行四边形
∵△AEF≌△DEB∴AF=BD
∴BD=CD,即AD是△ABC的中线
∵AB=AC ∴AD⊥BC ∴∠ADC=90°
∴ 四边形ADCF是矩形(定义法)
4.如图,△BDE中,BD=DE, C为BE中点, 四边形ACED是平行四边形.
求证:四边形ABCD是矩形.
证明:∵ C为BE的中点
∴BC=CE
∵四边形ACED是平行四边形
∴AC=DE AD∥CE且AD=CE
∴AD∥BC且AD=BC
∴四边形ABCD是平行四边形
∵AC=DE
又BD=DE
∴BD=AC
∴平行四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
1.在矩形ABCD中,M是CD的中点,P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的值可能是( )
A 3.2 B 3.5 C 3.6 D 3.8
解析:∵AP+PB=AB
∴PM最小时,PA+PB+PM的值是最小值,
由垂线段最短可知PM⊥CD时,PA+PB+PM的值是最小值,
最小值为1+2=3.当P在B点时PA+PB+PM=AB+BM=2+√2
≈ 3.4
∴PA+PB+PM的值范围为3≤PA+PB+PM<3.4,故选:A.
A
题型四 矩形中的动点问题
2.如图,在矩形ABCD中,AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,如果点P、Q分别从A. C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒。
(1)当t=2秒时,求P、Q两点之间的距离;
(2)t为何值时,线段AQ与DP互相平分
(3)t为何值时,四边形APQD的面积为矩形面积的
(1)如图所示:连接PQ,过点P作PE⊥DQ于点E,则DE=AP,PE=BC
∵AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,
∴当t=2秒时,QC=4cm,AP=8cm,
∴DQ=24 QC=20,则EQ=12,
∴PQ= = = (cm)
(2)∵AP=4t,DQ=24 2t,
当线段AQ与DP互相平分,则四边形APQD为矩形时,
则AP=DQ,即4t=24 2t,
解得:t=4.
故t为4秒时,线段AQ与DP互相平分
(3)∵P在AB上,
∴SAPQD= (DQ+AP)·AD,= (4t+24 2t)×10,=(10t+120)(cm2)(0
∴10t+120= ×240,
解得:t=3.
∴t为3秒时,四边形APQD的面积为矩形面积的 .
当堂检测
1.如图(左),在Rt△ABC中,∠ACB=90 ,D. E. F分别是AB、BC、CA的中点,若CD=5cm,则EF=___cm.
5
2.如图(右),Rt△ABC中,斜边BC上的高线AD=5cm,斜边BC上的中线AE=6cm,则△ABC的面积为______cm2.
30
3.如图(左),在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A. B.2 C. D.1
A
4.如图(右),△ABC是以AB为斜边的直角三角形,AC= 4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值为 .
2.4
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.
(1)求∠AOB的度数;
(2)若AB=2 cm,求矩形ABCD的面积.
解:(1)∵四边形ABCD是矩形,
∴AC=BD,∴BO=AO,∴∠OBA=∠OAB.
又∵AE⊥BD,且AE平分∠BAO,
∴∠BAE=1/2∠OAB,∠BAE+∠OBA=90°.
∴∠OBA=60°,
∴△AOB是等边三角形,
∴∠AOB=60°.
(2)∵△AOB是等边三角形,四边形ABCD是矩形
∴∠BAO=60°,∠ABC=90°∴∠ACB=30°.
∴AC=2AB=4 cm,BC= =2 cm.
∴S矩形ABCD=2×2 =4 (cm2).
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
证明:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,AC=BD
∵OD= BD,OC= AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO,
在△ODE与△OCF中,
DE=CF ∠EDO=∠FCO OD=OC,
∴△ODE≌△OCF(SAS),
∴OE=OF.
再 见
