九年级数学上册试题 2.6 应用一元二次方程-几何动态问题同步练习-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 2.6 应用一元二次方程-几何动态问题同步练习-北师大版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 751.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 23:22:38 | ||
图片预览




文档简介
2.6 应用一元二次方程-几何动态问题
一、填空题
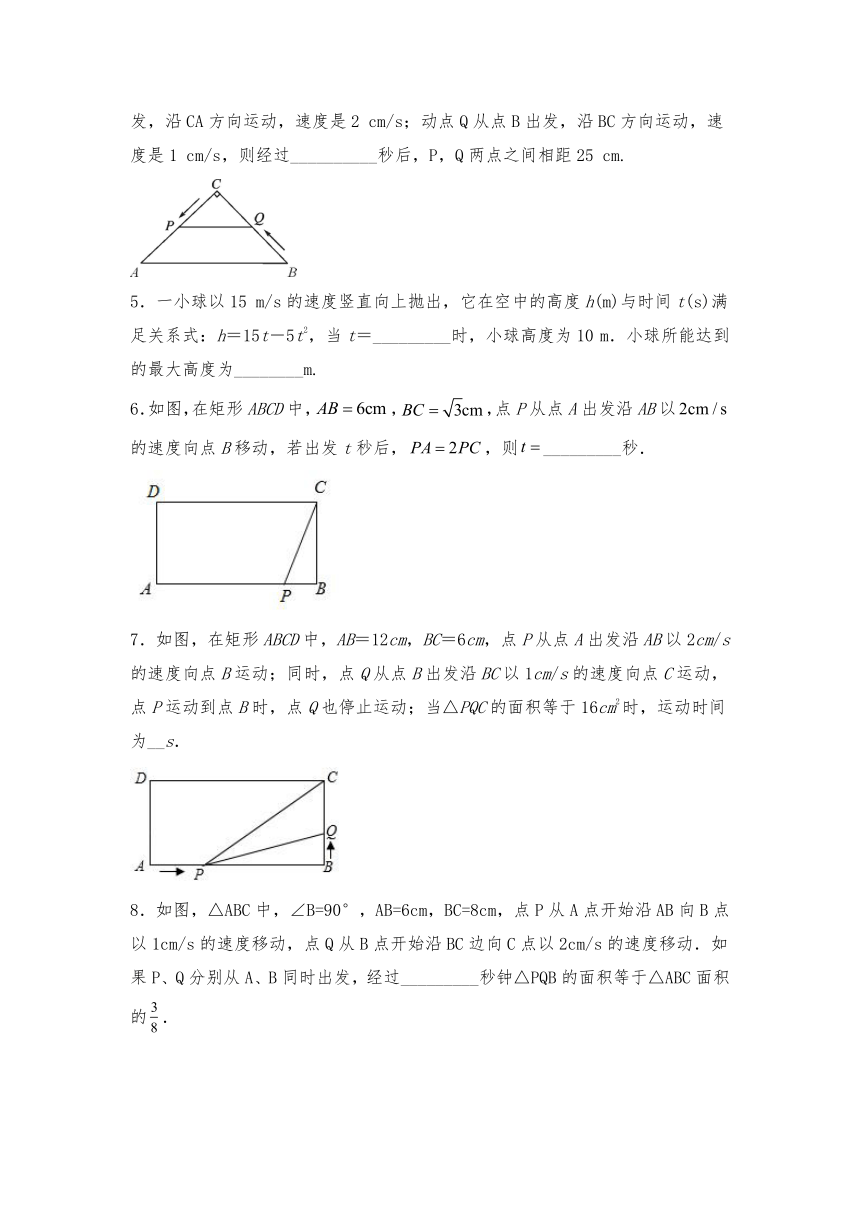
1.如图,在等腰中,,动点P从点A出发沿折线向点终B以的速度运动,于点Q.设运动时间为,当_______s时,的面积为.
2.如图,已知AB⊥BC,AB=12cm,BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动,同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动,其中一点到达B点时另一点也随之停止,当△MNB的面积为24cm2时运动的时间t为______秒.
3.如图,Rt△ABC中,AB=6,BC=8.点P从点A出发,以1个单位/秒的速度向B移动,同时,点Q从点B出发,以2个单位/秒的速度向点C移动,运动___秒后,△PBQ面积为5个平方单位.
4.如图,在Rt△ACB中,∠C=90°,AC=30 cm,BC=25 cm.动点P从点C出发,沿CA方向运动,速度是2 cm/s;动点Q从点B出发,沿BC方向运动,速度是1 cm/s,则经过__________秒后,P,Q两点之间相距25 cm.
一小球以15 m/s的速度竖直向上抛出,它在空中的高度h(m)与时间t(s)满足关系式:h=15t-5t2,当t=_________时,小球高度为10 m.小球所能达到的最大高度为________m.
6.如图,在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,若出发t秒后,,则_________秒.
7.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时,点Q从点B出发沿BC以1cm/s的速度向点C运动,点P运动到点B时,点Q也停止运动;当△PQC的面积等于16cm2时,运动时间为__s.
8.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动.如果P、Q分别从A、B同时出发,经过_________秒钟△PQB的面积等于△ABC面积的.
9.如图,在长方形ABCD中,AB=6cm,BC=10cm,若此长方形以2cm/s的速度沿着A→D方向移动,经过________秒平移后的长方形与原来长方形重叠部分的面积为24cm2.
10.如图,在Rt△ABC中,∠B=90°,AB=BC=12 cm,点D从点A开始沿边AB以2 cm/s的速度向点B移动,移动过程中始终保持四边形DFCE(点E,F分别在AC,BC上)为平行四边形,则出发________s时,四边形DFCE的面积为20 cm2.
11.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
12.如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
13.如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动,同时另一点Q从点C开始以3 cm/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300 cm2时,运动时间为__________.
14.设二次函数y=x2+ax+b图像与x轴有2个交点,A(x1,0),B(x2,0);且0< x1<1;1< x2<2,那么(1)a的取值范围是___________;b的取值范围是________;则(2)的取值范围是_______.
二、解答题
15.如图,中,,,,一动点从点出发沿着方向以的速度运动,另一动点从出发沿着边以的速度运动,,两点同时出发,运动时间为.
(1)若的面积是面积的,求的值?
(2)的面积能否为面积的一半?若能,求出的值;若不能,说明理由.
16.如图所示,在中,,点从点开始沿边向点以的速度移动,点Q从点开始沿着边向点以的速度移动.
(1)如果分别从同时出发,那么几秒后,的面积等于?
(2)小明在解答上述问题时,求得?请你判断一下,他做得对吗?并说明理由 .
17.如图,在中,,,,动点从点出发,沿方向运动,同时动点从点出发,沿方向运动,点,点的运动速度均为.当运动时间为多少秒时,两点相距?
18.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28cm2?若存在,请求出t的值;若不存在,请说明理由.
19.如图:在△ABC中,∠ABC=90°,AB=BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AB运动,同时动点Q从点C出发,以2cm/s的速度沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t秒,△PCQ的面积为S cm2.
(1)直接写出AC的长:AC= cm;
(2)求出S关于t的函数关系式,并求出当点P运动几秒时,S△PCQ=S△ABC
20.如图,在中,,,,点P从点A出发沿边AC向点以的速度移动,点Q从点出发沿CB边向点B以的速度移动.
(1)如果同时出发,几秒钟后,可使PQ的长为厘米?
(2)点在移动过程中,是否存在某一时刻,使得的面积等于的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
21.已知:如图所示,在中,,,,点P从点A开始沿AB边向点B以的速度移动,点Q从点B开始沿BC边向点C以的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,的面积等于?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于?
(3)的面积能否等于?请说明理由.
22.如图,中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.
(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
23.阅读以下材料,并按要求完成相应的任务.
给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,那么称这个矩形是给定矩形的“减半”矩形. 如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
任务:
当矩形的长为8,宽为1时,它是否存在“减半”矩形?如果存在,请求出“减半”矩形的长和宽;如果不存在,请说明理由.
24.如图,在矩形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ=__________cm,PB=_________cm;(用含t的代数式表示)
(2)当t为何值时,PQ的长度等于5cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
25.如图,已知中,,P、Q是边上的两个动点,其中点P从点A开始向B运动,且速度为每秒,点Q从点B开始沿方向运动,且速度为每秒.它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求的长:
(2)当点Q在边上运动时,出发几秒钟,能形成等腰三角形?
(3)当点Q在边上运动时,求能使成为等腰三角形的运动时间.
26.如图,矩形中,,,点从点出发沿向点移动(不与点、重合),一直到达点为止;同时,点从点出发沿向点移动(不与点、重合).
(1)若点、均以的速度移动,经过多长时间四边形为菱形?
(2)若点为的速度移动,点以的速度移动,经过多长时间为直角三角形?
27.如图,在四边形中,,,,,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,是否存在点P,使四边形是平行四边形,若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于;
(3)当时,是否存在点P,使是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
28.如图,平行四边形位于直角坐标系中,为坐标原点,点,点交轴于点 动点从点出发,沿方向以每秒1个单位长度的速度终点运动,同时动点从点出发,沿射线的方向以每秒2个单位长度的速度运动,当点运动到点时,点随之停止运动,运动时间为 t(秒).
(1)用t的代数式表示: ________, ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当恰好是等腰三角形时,求t的值.
29.如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
(1)问:运动______秒后,点P和点Q的距离是10cm.
(2)问几秒后,是否存在以PD为腰的等腰三角形?若存在,求出t值;若不存在,说明理由;
(3)问多少秒后,以P、Q、D三点为顶点的三角形为直角三角形?请写出计算过程.
答案
一、填空题
1.或
2.2.
3.1.
4.10.
5.1或2;.
6.4-.
7.2.
8.3.
9.3
10.1或5.
11..
12.或或或
13.5s
14. -3 a -1 0 b 2 2
二、填空题
15.
解:(1),,
,
,
解得:.
答:当时,的面积为面积的.
(2)的面积不可能是面积的一半.理由如下:
当时,
,
整理得:,
,
此方程没有实数根,
的面积不可能是面积的一半.
16.解:(1)设t秒后,的面积等于
t1=1,t2=4(不合题意,舍去)
答:1秒后,的面积等于
(2)不对
设t秒后,的面积等于8cm2
整理得:t2-5t+8=0
∵ b2-4ac=25-32=-7<0
∴此方程无解
∴ 的面积不能等于8cm2
17.解:设运动时间为秒时,,两点相距,
根据题意,得,
解得,,
答:运动时间为9秒或12秒时,,两点相距.
18.解:存在,t=2s或4s.理由如下:
可设x秒后△PDQ面积为28cm2,
即SABCD﹣S△ADP﹣S△PBQ﹣S△DCQ=12×6﹣×12x﹣(6﹣x) 2x﹣×6×(12﹣2x)=28,
解得x1=2,x2=4,
当其运动2秒或4秒时均符合题意,
所以2秒或4秒时面积为28cm2.
19.解:(1)在Rt△ABC中,∠ABC=90°,AB=BC=8cm,
∴AC==8 cm.
故答案为:8;
(2)∵AP=CQ=2t,AB=8,
∴BP=|8 2t|,
∴S=CQ BP=t|8 2t|,
即S=.
当0<t≤4时, 2t2+8t=AB×BC=×8×8,
整理,得:t2 4t+16=0,
∵△=( 4)2 4×1×16= 48<0,
∴该方程无解;
当t>4时,2t2 8t=×8×8,
整理,得:t2 4t 16=0,
解得:t1=2 2(不合题意,舍去),t2=2+2.
∴当点P运动(2+2)秒时,S△PCQ=S△ABC.
20.解:(1)设x秒钟后,可使PQ的长为厘米,由题意得:
,
解得:x=2或x=,
答:同时出发2或秒钟后,可使PQ的长为厘米;
(2)不存在.
理由:设y秒时,△PCQ的面积等于△ABC的面积的一半,由题意得:
,
y2 6y+12=0,
∵△=36 4×12<0,
∴方程无解,即:不存在.
21.解:(1)设经过x秒以后,面积为,
此时,,,
由得,
整理得:,
解得:或舍,
答:1秒后的面积等于 ;
(2)设经过t秒后,PQ的长度等于
由,
即,
解得:t=3或-1(舍),
∴3秒后,PQ的长度为;
(3)假设经过t秒后,的面积等于,
即,,
整理得:,
由于,
则原方程没有实数根,
∴的面积不能等于.
22.解:(1)P、Q同时出发,经过秒钟,,
由题意得:
∴,
解得:,.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4秒点P到离A点1×4=4cm处,点Q到离C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2秒或4秒,.
(2)设P出发t秒时,则Q运动的时间为秒,由题意得:
,
∴,
解得:.
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4﹣2)=4cm,符合题意.
答:P先出发2秒,Q再从C出发,经过2秒后.
(3)设经过秒钟后PQ=BQ,则,,,
,
解得:,(不合题意,舍去),
答:经过秒钟后PQ=BQ.
23.解:假设存在,设“减半”矩形的长为x,则宽为(﹣x),
依题意,得:x(﹣x)=×8×1,
整理,得:x2﹣x+4=0,
解得:x1=,x2=.
当x=时,﹣x=,符合题意;
当x=时,﹣x=>,不合题意,舍去.
∴长为8,宽为1的矩形存在“减半”矩形,且“减半”矩形的长为,宽为.
24.解:(1)∵P从点A开始沿边AB向终点B以1cm/s的速度移动,
∴AP=tcm,
∵AB=5cm,
∴PB=(5-t)cm,
∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动,
∴BQ=2tcm;
(2)由题意得:(5-t)2+(2t)2=52,
解得:t1=0,t2=2;
当t=0秒或2秒时,PQ的长度等于5cm;
(3)存在t=1秒,能够使得五边形APQCD的面积等于26cm2.理由如下:
长方形ABCD的面积是:5×6=30(cm2),
使得五边形APQCD的面积等于26cm2,则△PBQ的面积为30-26=4(cm2),
(5-t)×2t×=4,
解得:t1=4(不合题意舍去),t2=1.
即当t=1秒时,使得五边形APQCD的面积等于26cm2.
25.解:(1)当t=2时,则AP=2,BQ=2t=4,
∵AB=8cm,
∴BP=AB-AP=8-2=6(cm),
在Rt△BPQ中,由勾股定理可得PQ=cm,
即PQ的长为cm;
(2)由题意可知AP=t,BQ=2t,
∵AB=8,
∴BP=AB-AP=8-t,
当△PQB为等腰三角形时,则有BP=BQ,即8-t=2t,
解得t=,
∴出发秒后△PQB能形成等腰三角形;
(3)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,
∴CQ=AC-AQ=10-(16-2t)=2t-6,
∵△BCQ为等腰三角形,
∴有BQ=BC、CQ=BC和CQ=BQ三种情况,
①当BQ=BC=6时,如图1,过B作BD⊥AC,
则CD=CQ=t-3,在Rt△ABC中,求得BD=,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=()2+(t-3)2,
解得t=6.6或t=-0.6<0(舍去);
②当CQ=BC=6时,则2t-6=6,解得t=6;
③当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,
∴∠A=∠QBA,
∴QB=QA,
∴CQ=AC=5,即2t-6=5,解得t=5.5;
综上可知:当运动时间为6.6秒或6秒或5.5秒时,△BCQ为等腰三角形.
26.解:(1)由题可知,
由于P、Q两点速度大小相同,
,
是平行四边形,
当时,四边形是菱形;
设经过了x秒四边形是菱形,则有:
,
由勾股定理得:
解得:
故经过秒四边形是菱形;
(2) P、A两点不重合
为直角三角形有两种情况:①当时过Q作于M,可知为矩形,如图所示
,,则有:
,
解得:, ;
②当时,,
所以,解得 ;
综上可知:经过2秒、秒 、秒时为直角三角形.
27.解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,
∵DQ=AD-AQ=16-t,
CP=21-2t,
∴16-t=21-2t,
解得t=5,
∴当t=5秒时,四边形PQDC是平行四边形;
(2)若点P、Q分别沿AD、BC运动时,
AB=60,
即×12=60,
解得t=9(秒),
若点P返回时,CP=2t-21,
则×12=60,
解得t=15(秒).
故当t=9秒或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
(3)当PQ=PD时,
作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16-t),
∵AH=BP,
∴2t=(16-t)+t,
∴t=秒;
当PQ=QD时,QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=t2+122,
∴(16-t)2=122+t2,
解得t=(秒);
当QD=PD时,DH=AD-AH=AD-BP=16-2t,
∵QD2=PD2=PH2+HD2=122+(16-2t)2,
∴(16-t)2=122+(16-2t)2,
即3t2-32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒时,△PQD是等腰三角形.
28.解:(1)如图
根据题意,可得点B的坐标为( 5,4),点,
∴BD=BC-CD=8-3=5,
BE=BD-DE=5-t;
OF=2t
故答案为BE=5-t,OF=2t.
(2)解:①当F在A点右侧,四边形ABEF为平行四边形,
,
即,
解得,
②当F在A点左侧,四边形BEAF为平行四边形,
,即,
解得;
(3)解:当恰好是等腰三角形时,过点B作BJ⊥x轴于J,过点E作EK⊥x轴于K,
BE=5-t,
EF=,
BF=,
有以下三种情况:
①当时,有=,
,
解得;
②当时,
有,
△=100-4×3×16=-92<0,故方程无解;
③当时,有,
解得;
所以,当或时,恰好是等腰三角形.
29.解:(1)如图,过点P作PE⊥CD,垂足为E,由QE=|(16-3t)-2t|,
由勾股定理得|(16-3t)-2t|2+62=102,
即(16-5t)2=64,16-5t=±8.
∴t=或,
所以当t=或时,点P和点Q的距离是10cm;
(2)当DP=DQ时,则DM=MQ=3tcm.
∵3t+3t+2t=16.
∴t=2;
当DP=DQ时,在直角△DAP中,
由勾股定理得:(16-2t)2=62+(3t)2,
解得t1=,t2=(舍去),
综上所述,经过2秒、秒时,点P、Q、D组成的三角形是以PD为腰的等腰三角形.
(3)∵点P不与点A重合,
∴∠PDQ≠90°,
∴△DPQ为直角三角形分两种情况:
①当∠DPQ=90°时,△DPQ为直角三角形,过点Q作QM⊥AB于M,可得四边形BCQM为矩形,如图所示.
∵AP=3xcm,BM=CQ=2xcm,则PM=(16-5x)cm,DQ=(16-2x)cm,
∴(16-5x)2+62+(3x)2+62=(16-2x)2,
解得:x1=2,x2=;
②当∠DQP=90°时,AP+CQ=16,
所以3x+2x=16,解得:x=,
综上可知:经过2s、s、s时,以P、Q、D三点为顶点的三角形为直角三角形.
一、填空题
1.如图,在等腰中,,动点P从点A出发沿折线向点终B以的速度运动,于点Q.设运动时间为,当_______s时,的面积为.
2.如图,已知AB⊥BC,AB=12cm,BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动,同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动,其中一点到达B点时另一点也随之停止,当△MNB的面积为24cm2时运动的时间t为______秒.
3.如图,Rt△ABC中,AB=6,BC=8.点P从点A出发,以1个单位/秒的速度向B移动,同时,点Q从点B出发,以2个单位/秒的速度向点C移动,运动___秒后,△PBQ面积为5个平方单位.
4.如图,在Rt△ACB中,∠C=90°,AC=30 cm,BC=25 cm.动点P从点C出发,沿CA方向运动,速度是2 cm/s;动点Q从点B出发,沿BC方向运动,速度是1 cm/s,则经过__________秒后,P,Q两点之间相距25 cm.
一小球以15 m/s的速度竖直向上抛出,它在空中的高度h(m)与时间t(s)满足关系式:h=15t-5t2,当t=_________时,小球高度为10 m.小球所能达到的最大高度为________m.
6.如图,在矩形ABCD中,,,点P从点A出发沿AB以的速度向点B移动,若出发t秒后,,则_________秒.
7.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时,点Q从点B出发沿BC以1cm/s的速度向点C运动,点P运动到点B时,点Q也停止运动;当△PQC的面积等于16cm2时,运动时间为__s.
8.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动.如果P、Q分别从A、B同时出发,经过_________秒钟△PQB的面积等于△ABC面积的.
9.如图,在长方形ABCD中,AB=6cm,BC=10cm,若此长方形以2cm/s的速度沿着A→D方向移动,经过________秒平移后的长方形与原来长方形重叠部分的面积为24cm2.
10.如图,在Rt△ABC中,∠B=90°,AB=BC=12 cm,点D从点A开始沿边AB以2 cm/s的速度向点B移动,移动过程中始终保持四边形DFCE(点E,F分别在AC,BC上)为平行四边形,则出发________s时,四边形DFCE的面积为20 cm2.
11.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
12.如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
13.如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动,同时另一点Q从点C开始以3 cm/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300 cm2时,运动时间为__________.
14.设二次函数y=x2+ax+b图像与x轴有2个交点,A(x1,0),B(x2,0);且0< x1<1;1< x2<2,那么(1)a的取值范围是___________;b的取值范围是________;则(2)的取值范围是_______.
二、解答题
15.如图,中,,,,一动点从点出发沿着方向以的速度运动,另一动点从出发沿着边以的速度运动,,两点同时出发,运动时间为.
(1)若的面积是面积的,求的值?
(2)的面积能否为面积的一半?若能,求出的值;若不能,说明理由.
16.如图所示,在中,,点从点开始沿边向点以的速度移动,点Q从点开始沿着边向点以的速度移动.
(1)如果分别从同时出发,那么几秒后,的面积等于?
(2)小明在解答上述问题时,求得?请你判断一下,他做得对吗?并说明理由 .
17.如图,在中,,,,动点从点出发,沿方向运动,同时动点从点出发,沿方向运动,点,点的运动速度均为.当运动时间为多少秒时,两点相距?
18.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28cm2?若存在,请求出t的值;若不存在,请说明理由.
19.如图:在△ABC中,∠ABC=90°,AB=BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AB运动,同时动点Q从点C出发,以2cm/s的速度沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t秒,△PCQ的面积为S cm2.
(1)直接写出AC的长:AC= cm;
(2)求出S关于t的函数关系式,并求出当点P运动几秒时,S△PCQ=S△ABC
20.如图,在中,,,,点P从点A出发沿边AC向点以的速度移动,点Q从点出发沿CB边向点B以的速度移动.
(1)如果同时出发,几秒钟后,可使PQ的长为厘米?
(2)点在移动过程中,是否存在某一时刻,使得的面积等于的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
21.已知:如图所示,在中,,,,点P从点A开始沿AB边向点B以的速度移动,点Q从点B开始沿BC边向点C以的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,的面积等于?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于?
(3)的面积能否等于?请说明理由.
22.如图,中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.
(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
23.阅读以下材料,并按要求完成相应的任务.
给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,那么称这个矩形是给定矩形的“减半”矩形. 如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
任务:
当矩形的长为8,宽为1时,它是否存在“减半”矩形?如果存在,请求出“减半”矩形的长和宽;如果不存在,请说明理由.
24.如图,在矩形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ=__________cm,PB=_________cm;(用含t的代数式表示)
(2)当t为何值时,PQ的长度等于5cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
25.如图,已知中,,P、Q是边上的两个动点,其中点P从点A开始向B运动,且速度为每秒,点Q从点B开始沿方向运动,且速度为每秒.它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求的长:
(2)当点Q在边上运动时,出发几秒钟,能形成等腰三角形?
(3)当点Q在边上运动时,求能使成为等腰三角形的运动时间.
26.如图,矩形中,,,点从点出发沿向点移动(不与点、重合),一直到达点为止;同时,点从点出发沿向点移动(不与点、重合).
(1)若点、均以的速度移动,经过多长时间四边形为菱形?
(2)若点为的速度移动,点以的速度移动,经过多长时间为直角三角形?
27.如图,在四边形中,,,,,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,是否存在点P,使四边形是平行四边形,若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于;
(3)当时,是否存在点P,使是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
28.如图,平行四边形位于直角坐标系中,为坐标原点,点,点交轴于点 动点从点出发,沿方向以每秒1个单位长度的速度终点运动,同时动点从点出发,沿射线的方向以每秒2个单位长度的速度运动,当点运动到点时,点随之停止运动,运动时间为 t(秒).
(1)用t的代数式表示: ________, ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当恰好是等腰三角形时,求t的值.
29.如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
(1)问:运动______秒后,点P和点Q的距离是10cm.
(2)问几秒后,是否存在以PD为腰的等腰三角形?若存在,求出t值;若不存在,说明理由;
(3)问多少秒后,以P、Q、D三点为顶点的三角形为直角三角形?请写出计算过程.
答案
一、填空题
1.或
2.2.
3.1.
4.10.
5.1或2;.
6.4-.
7.2.
8.3.
9.3
10.1或5.
11..
12.或或或
13.5s
14. -3 a -1 0 b 2 2
二、填空题
15.
解:(1),,
,
,
解得:.
答:当时,的面积为面积的.
(2)的面积不可能是面积的一半.理由如下:
当时,
,
整理得:,
,
此方程没有实数根,
的面积不可能是面积的一半.
16.解:(1)设t秒后,的面积等于
t1=1,t2=4(不合题意,舍去)
答:1秒后,的面积等于
(2)不对
设t秒后,的面积等于8cm2
整理得:t2-5t+8=0
∵ b2-4ac=25-32=-7<0
∴此方程无解
∴ 的面积不能等于8cm2
17.解:设运动时间为秒时,,两点相距,
根据题意,得,
解得,,
答:运动时间为9秒或12秒时,,两点相距.
18.解:存在,t=2s或4s.理由如下:
可设x秒后△PDQ面积为28cm2,
即SABCD﹣S△ADP﹣S△PBQ﹣S△DCQ=12×6﹣×12x﹣(6﹣x) 2x﹣×6×(12﹣2x)=28,
解得x1=2,x2=4,
当其运动2秒或4秒时均符合题意,
所以2秒或4秒时面积为28cm2.
19.解:(1)在Rt△ABC中,∠ABC=90°,AB=BC=8cm,
∴AC==8 cm.
故答案为:8;
(2)∵AP=CQ=2t,AB=8,
∴BP=|8 2t|,
∴S=CQ BP=t|8 2t|,
即S=.
当0<t≤4时, 2t2+8t=AB×BC=×8×8,
整理,得:t2 4t+16=0,
∵△=( 4)2 4×1×16= 48<0,
∴该方程无解;
当t>4时,2t2 8t=×8×8,
整理,得:t2 4t 16=0,
解得:t1=2 2(不合题意,舍去),t2=2+2.
∴当点P运动(2+2)秒时,S△PCQ=S△ABC.
20.解:(1)设x秒钟后,可使PQ的长为厘米,由题意得:
,
解得:x=2或x=,
答:同时出发2或秒钟后,可使PQ的长为厘米;
(2)不存在.
理由:设y秒时,△PCQ的面积等于△ABC的面积的一半,由题意得:
,
y2 6y+12=0,
∵△=36 4×12<0,
∴方程无解,即:不存在.
21.解:(1)设经过x秒以后,面积为,
此时,,,
由得,
整理得:,
解得:或舍,
答:1秒后的面积等于 ;
(2)设经过t秒后,PQ的长度等于
由,
即,
解得:t=3或-1(舍),
∴3秒后,PQ的长度为;
(3)假设经过t秒后,的面积等于,
即,,
整理得:,
由于,
则原方程没有实数根,
∴的面积不能等于.
22.解:(1)P、Q同时出发,经过秒钟,,
由题意得:
∴,
解得:,.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4秒点P到离A点1×4=4cm处,点Q到离C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2秒或4秒,.
(2)设P出发t秒时,则Q运动的时间为秒,由题意得:
,
∴,
解得:.
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4﹣2)=4cm,符合题意.
答:P先出发2秒,Q再从C出发,经过2秒后.
(3)设经过秒钟后PQ=BQ,则,,,
,
解得:,(不合题意,舍去),
答:经过秒钟后PQ=BQ.
23.解:假设存在,设“减半”矩形的长为x,则宽为(﹣x),
依题意,得:x(﹣x)=×8×1,
整理,得:x2﹣x+4=0,
解得:x1=,x2=.
当x=时,﹣x=,符合题意;
当x=时,﹣x=>,不合题意,舍去.
∴长为8,宽为1的矩形存在“减半”矩形,且“减半”矩形的长为,宽为.
24.解:(1)∵P从点A开始沿边AB向终点B以1cm/s的速度移动,
∴AP=tcm,
∵AB=5cm,
∴PB=(5-t)cm,
∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动,
∴BQ=2tcm;
(2)由题意得:(5-t)2+(2t)2=52,
解得:t1=0,t2=2;
当t=0秒或2秒时,PQ的长度等于5cm;
(3)存在t=1秒,能够使得五边形APQCD的面积等于26cm2.理由如下:
长方形ABCD的面积是:5×6=30(cm2),
使得五边形APQCD的面积等于26cm2,则△PBQ的面积为30-26=4(cm2),
(5-t)×2t×=4,
解得:t1=4(不合题意舍去),t2=1.
即当t=1秒时,使得五边形APQCD的面积等于26cm2.
25.解:(1)当t=2时,则AP=2,BQ=2t=4,
∵AB=8cm,
∴BP=AB-AP=8-2=6(cm),
在Rt△BPQ中,由勾股定理可得PQ=cm,
即PQ的长为cm;
(2)由题意可知AP=t,BQ=2t,
∵AB=8,
∴BP=AB-AP=8-t,
当△PQB为等腰三角形时,则有BP=BQ,即8-t=2t,
解得t=,
∴出发秒后△PQB能形成等腰三角形;
(3)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,
∴CQ=AC-AQ=10-(16-2t)=2t-6,
∵△BCQ为等腰三角形,
∴有BQ=BC、CQ=BC和CQ=BQ三种情况,
①当BQ=BC=6时,如图1,过B作BD⊥AC,
则CD=CQ=t-3,在Rt△ABC中,求得BD=,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=()2+(t-3)2,
解得t=6.6或t=-0.6<0(舍去);
②当CQ=BC=6时,则2t-6=6,解得t=6;
③当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,
∴∠A=∠QBA,
∴QB=QA,
∴CQ=AC=5,即2t-6=5,解得t=5.5;
综上可知:当运动时间为6.6秒或6秒或5.5秒时,△BCQ为等腰三角形.
26.解:(1)由题可知,
由于P、Q两点速度大小相同,
,
是平行四边形,
当时,四边形是菱形;
设经过了x秒四边形是菱形,则有:
,
由勾股定理得:
解得:
故经过秒四边形是菱形;
(2) P、A两点不重合
为直角三角形有两种情况:①当时过Q作于M,可知为矩形,如图所示
,,则有:
,
解得:, ;
②当时,,
所以,解得 ;
综上可知:经过2秒、秒 、秒时为直角三角形.
27.解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,
∵DQ=AD-AQ=16-t,
CP=21-2t,
∴16-t=21-2t,
解得t=5,
∴当t=5秒时,四边形PQDC是平行四边形;
(2)若点P、Q分别沿AD、BC运动时,
AB=60,
即×12=60,
解得t=9(秒),
若点P返回时,CP=2t-21,
则×12=60,
解得t=15(秒).
故当t=9秒或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
(3)当PQ=PD时,
作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16-t),
∵AH=BP,
∴2t=(16-t)+t,
∴t=秒;
当PQ=QD时,QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=t2+122,
∴(16-t)2=122+t2,
解得t=(秒);
当QD=PD时,DH=AD-AH=AD-BP=16-2t,
∵QD2=PD2=PH2+HD2=122+(16-2t)2,
∴(16-t)2=122+(16-2t)2,
即3t2-32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒时,△PQD是等腰三角形.
28.解:(1)如图
根据题意,可得点B的坐标为( 5,4),点,
∴BD=BC-CD=8-3=5,
BE=BD-DE=5-t;
OF=2t
故答案为BE=5-t,OF=2t.
(2)解:①当F在A点右侧,四边形ABEF为平行四边形,
,
即,
解得,
②当F在A点左侧,四边形BEAF为平行四边形,
,即,
解得;
(3)解:当恰好是等腰三角形时,过点B作BJ⊥x轴于J,过点E作EK⊥x轴于K,
BE=5-t,
EF=,
BF=,
有以下三种情况:
①当时,有=,
,
解得;
②当时,
有,
△=100-4×3×16=-92<0,故方程无解;
③当时,有,
解得;
所以,当或时,恰好是等腰三角形.
29.解:(1)如图,过点P作PE⊥CD,垂足为E,由QE=|(16-3t)-2t|,
由勾股定理得|(16-3t)-2t|2+62=102,
即(16-5t)2=64,16-5t=±8.
∴t=或,
所以当t=或时,点P和点Q的距离是10cm;
(2)当DP=DQ时,则DM=MQ=3tcm.
∵3t+3t+2t=16.
∴t=2;
当DP=DQ时,在直角△DAP中,
由勾股定理得:(16-2t)2=62+(3t)2,
解得t1=,t2=(舍去),
综上所述,经过2秒、秒时,点P、Q、D组成的三角形是以PD为腰的等腰三角形.
(3)∵点P不与点A重合,
∴∠PDQ≠90°,
∴△DPQ为直角三角形分两种情况:
①当∠DPQ=90°时,△DPQ为直角三角形,过点Q作QM⊥AB于M,可得四边形BCQM为矩形,如图所示.
∵AP=3xcm,BM=CQ=2xcm,则PM=(16-5x)cm,DQ=(16-2x)cm,
∴(16-5x)2+62+(3x)2+62=(16-2x)2,
解得:x1=2,x2=;
②当∠DQP=90°时,AP+CQ=16,
所以3x+2x=16,解得:x=,
综上可知:经过2s、s、s时,以P、Q、D三点为顶点的三角形为直角三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
