七年级数学上册试题 第四章 基本平面图形B卷-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第四章 基本平面图形B卷-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 556.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 14:17:09 | ||
图片预览



文档简介
第四章 基本平面图形B卷
一、选择题(本大题共10个小题,每小题3分,共30分)
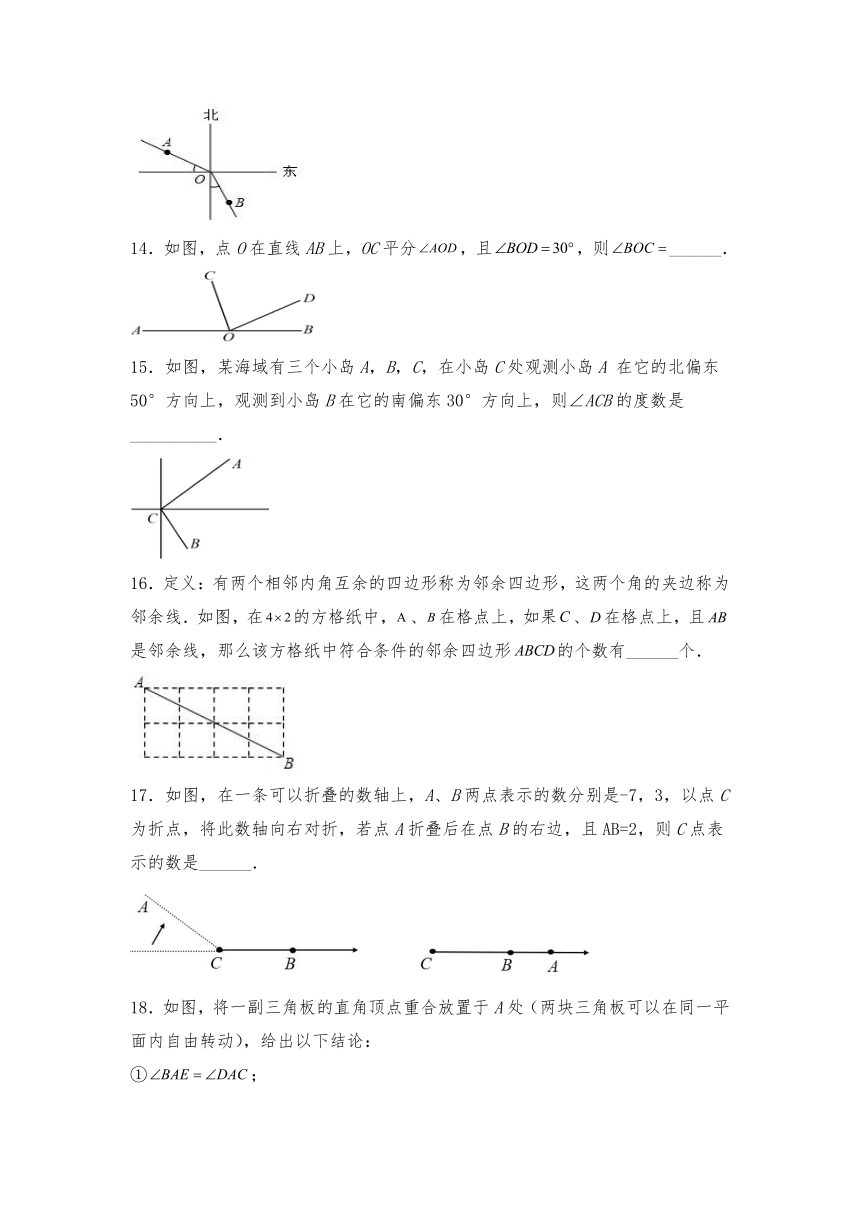
1.如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若,则线段AB的长为( )
A.12 B.10 C.8 D.7
2.如图,已知直线上顺次三个点、、,已知,.是的中点,是的中点,那么( ).
A.4 B.3 C.2 D.1
3.如图,小玮从A处沿北偏东40°方向行走到点B处,又从点B处沿东偏南23°方向行走到点C处,则∠ABC的度数为( )
A.99° B.107° C.127° D.129°
4.如图,是一副三角板的摆放图,将一个三角板60°的角的顶点与另一个三角板的直角顶点重合,,则的大小是( ).
A.60° B.50° C.40° D.30°
5.将一张长方形纸片按如图所示方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、,若,则的度数为( )
A.40.5° B.41° C.41.5° D.42°
6.如图是一个正方体的展开图,则“学”字对面的字是( )
A.初 B.美 C.审 D.中
7.如图,直线l上有A,B,C,D四点,点P从点A的左侧沿直线l从左向右运动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,点P就称为这两个点的黄金伴侣点,例:若PA=PB,则在点P从左向右运动的过程中,点P成为黄金伴侣点的机会有( )
A.4次 B.5次 C.6次 D.7次
8.点的位置如图所示,则从点观察点的位置是( )
A.距点处 B.北偏东方向处
C.东偏北方向处 D.北偏东方向处
9.如图,C、D是线段AB上两点,M、N分别是线段AD、BC的中点,下列结论:①若AD=BM,则AB=3BD;②若AC=BD,则AM=BN;③AC-BD=2(MC-DN);④2MN=AB-CD.其中正确的结论是( )
A.①②③ B.③④ C.①②④ D.①②③④
10.今年是牛年,在班级“牛年拼牛画”的活动中,小刚同学用一个边长为8cm的正方形做成的七巧板(如图1)拼成了一头牛的图案(如图2),则牛头部所占的面积为( )
A.4 cm2 B.8 cm2 C.16 cm2 D.20 cm2
二、填空题(本大题共8个小题,每题2分,共16分)
11.如图,AB=6cm,点C是线段AB的中点,点D在CB上且CD=DB,则AD=____cm.
12.如图,有一种电子游戏,电子屏幕上有一条直线l,在直线上有A,B,C,D四点,且AB=BC=CD.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有______个.
13.如图,点在点的北偏西80°方向上,点在点的南偏东20°的方向上,则________°.
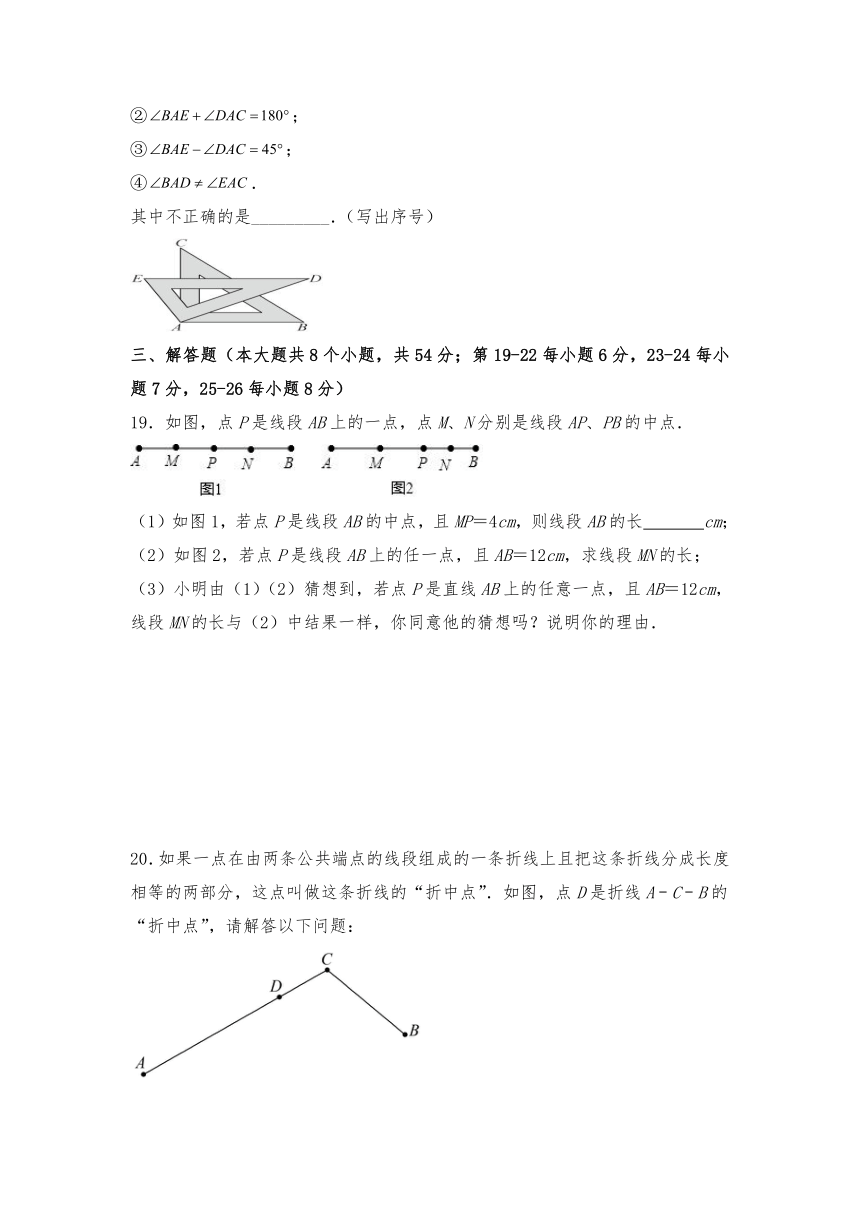
14.如图,点O在直线AB上,OC平分,且,则______.
15.如图,某海域有三个小岛A,B,C,在小岛C处观测小岛A 在它的北偏东50°方向上,观测到小岛B在它的南偏东30°方向上,则∠ACB的度数是__________.
16.定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.如图,在的方格纸中,、在格点上,如果、在格点上,且是邻余线,那么该方格纸中符合条件的邻余四边形的个数有______个.
17.如图,在一条可以折叠的数轴上,A、B两点表示的数分别是-7,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且AB=2,则C点表示的数是______.
18.如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),给出以下结论:
①;
②;
③;
④.
其中不正确的是_________.(写出序号)
三、解答题(本大题共8个小题,共54分;第19-22每小题6分,23-24每小题7分,25-26每小题8分)
19.如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,则线段AB的长 cm;
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长;
(3)小明由(1)(2)猜想到,若点P是直线AB上的任意一点,且AB=12cm,线段MN的长与(2)中结果一样,你同意他的猜想吗?说明你的理由.
20.如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:
(1)当AC>BC时,点D在线段 上;当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)当AC<BC时,若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
21.如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
22.(1)如图,由若干个大小相同的小正方体堆砌而成的几何体,请你画出该几何体从左面、上面看到的形状图
(2)如图,已知线段,点是线段的中点,先按要求补全图形(保留痕迹).
①延长线段至点,使;延长线段至点,使;
②若点是线段的中点,求线段PB的长度.
23.直线l上的三个点A、B、C,若满足BC=AB,则称点C是点A关于点B的“半距点”.如图1,BC=AB,此时点C就是点A关于点B的一个“半距点”.
若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm.
(1)
(2)若点G也是直线m上一点,且点G是线段MP的中点,求线段GN的长度.
24.如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一块直角三角板DOE直角顶点放在点O处.
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=____________°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠BOD、∠COE的度数;
(3)如图3,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
25.多多对几何中角平分线等兴趣浓厚,请你和多多一起探究下面问题吧.已知∠AOB=100°,射线OE,OF分别是∠AOC和∠COB的角平分线.
(1)如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;
(2)如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数_____;
(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数(不写探究过程).
26.斐波那契数列是数学家莱昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13…也就是从第三个数开始,每一个数都是前两个数的和. 如图所示的长方形是由几个正方形依次拼接而成,其中最小的正方形的边长为1.
(1)如图1中最大的正方形的边长是_________.
(2)如图2所示,在小正方形中画弧,将6段圆弧依次连接起来得到曲线ABCDEFG,求曲线ABCDEFG的长.
(3)如果按此规律继续画弧,将9段圆弧依次连起来得到的曲线的长为____.
答案
一、选择题
C.C.B.B.B.C.C.D.DC.
二、填空题
11.4.
12.5.
13.120
14.105°.
15.100°.
16.6.
17.-1.
18.①③④
三、解答题
19.解:(1)∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∵MP=4cm,
∴AP=8cm,
∵P为AB的中点,
∴AB=2AP=16cm,
故答案为:16;
(2)∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴AP+BP=2MP+2PN=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm;
(3)同意.
理由:当P点在线段AB延长线上时,
∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴AP-BP=2MP-2PN=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm;
当P点在线段BA延长线上时,
∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴BP-AP=2PN-2MP=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm.
20.(1)解:当AC>BC时,由“折中点”的定义可知点D在线段AC上;
当AC=BC时,点D与点C重合
当AC<BC时,点D在线段BC上
(2)
如下图,∵ E为线段AC中点
∴ AE=EC=8cm
∴ BD=AE+EC+CD=8+8+6=22(cm)
∴ CB=BD+DC=22+6=28(cm)
21.(1)∵∠NPA = 40°, ∠MPB = 30°,∠MPC = 70°,
∴∠BPC = ∠MPB + ∠MPC = 30°+70°= 100°,
∵PE平分∠BPC,
∴∠BPE =∠BPC =×100°=50°,
∴∠APB =180°-∠NPA-∠MPB = 180°-40°-30°=110°,
∴∠APE = ∠BPE + ∠APB = 50°+ 110°= 160° ,
(2)∵∠MPD = ∠BPE -∠MPB = 50°-30°= 20°,
∴轮船D在灯塔P北偏西20°的方位上 .
22.(1)如图,
(2)①如图,
②∵AM=2MN,MN=2,
∴AM=4,
∵P是AM的中点,
∴PM=AM=2,
∵,
∴BN=MN=1,
∴PB=PM+MN+BN=2+2+1=5.
23.(1)如图所示:
第一种情况:
∵ 点P是点M关于点N的“半距点”,
∴ ,
∵,
∴
第二种情况:
∵,
∴
综上:MP的长度为3cm或9cm
(2)如图所示:
第一种情况:
点是线段的中点,
∴
∴
第二种情况:
点是线段的中点,
∴
∴
综上:线段GN的长度为或.
24.(1)解:如图①,∠COE=∠DOE-∠BOC=90°-70°=20°,
故答案为:20;
(2)
如图②,∵OC平分∠EOB,∠BOC=70°,
∴∠EOB=2∠BOC=140°,
∵∠DOE=90°,
∴∠BOD=∠BOE-∠DOE=50°,
∵∠BOC=70°,
∴∠COD=∠BOC-∠BOD=20°,
∴∠COE=∠EOD-∠COD=70°;
(3)
∠COE-∠BOD=20°
理由是:如图③,∵∠BOD+∠COD=∠BOC=70°,∠COE+∠COD=∠DOE=90°,
∴(∠COE+∠COD)-(∠BOD+∠COD)
=∠COE+∠COD-∠BOD-∠COD
=∠COE-∠BOD
=90°-70°
=20°,
即∠COE-∠BOD=20°.
25.(1)
解: 是的平分线,,
,
,
,
是的平分线,
,
;
(2)
,
,
是的平分线,是的平分线,
,
故答案为:
(3)
是的平分线,是的平分线,
,
由题意,分以下三种情况:
①如图,延长至点,当射线在的内部时,
,
,
;
②如图,延长至点,延长至点,当射线在的内部时,
,
,
;
③如图,延长至点,当射线在的内部时,
,
,
;
综上,的度数为或.
26.(1)解:∵=1,
由图1知,是数列中的第六项,
∴=8,
故答案为:8;
(2)解:由图2可知,每个小正方形内的圆弧的半径都为这个小正方形的边长,
则
…
∴
∴曲线ABCDEFG的长为10π;
(3)解:根据题意得:按此规律继续画弧,将9段圆弧依次连起来得到的曲线的长为:
故答案为:44.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若,则线段AB的长为( )
A.12 B.10 C.8 D.7
2.如图,已知直线上顺次三个点、、,已知,.是的中点,是的中点,那么( ).
A.4 B.3 C.2 D.1
3.如图,小玮从A处沿北偏东40°方向行走到点B处,又从点B处沿东偏南23°方向行走到点C处,则∠ABC的度数为( )
A.99° B.107° C.127° D.129°
4.如图,是一副三角板的摆放图,将一个三角板60°的角的顶点与另一个三角板的直角顶点重合,,则的大小是( ).
A.60° B.50° C.40° D.30°
5.将一张长方形纸片按如图所示方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、,若,则的度数为( )
A.40.5° B.41° C.41.5° D.42°
6.如图是一个正方体的展开图,则“学”字对面的字是( )
A.初 B.美 C.审 D.中
7.如图,直线l上有A,B,C,D四点,点P从点A的左侧沿直线l从左向右运动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,点P就称为这两个点的黄金伴侣点,例:若PA=PB,则在点P从左向右运动的过程中,点P成为黄金伴侣点的机会有( )
A.4次 B.5次 C.6次 D.7次
8.点的位置如图所示,则从点观察点的位置是( )
A.距点处 B.北偏东方向处
C.东偏北方向处 D.北偏东方向处
9.如图,C、D是线段AB上两点,M、N分别是线段AD、BC的中点,下列结论:①若AD=BM,则AB=3BD;②若AC=BD,则AM=BN;③AC-BD=2(MC-DN);④2MN=AB-CD.其中正确的结论是( )
A.①②③ B.③④ C.①②④ D.①②③④
10.今年是牛年,在班级“牛年拼牛画”的活动中,小刚同学用一个边长为8cm的正方形做成的七巧板(如图1)拼成了一头牛的图案(如图2),则牛头部所占的面积为( )
A.4 cm2 B.8 cm2 C.16 cm2 D.20 cm2
二、填空题(本大题共8个小题,每题2分,共16分)
11.如图,AB=6cm,点C是线段AB的中点,点D在CB上且CD=DB,则AD=____cm.
12.如图,有一种电子游戏,电子屏幕上有一条直线l,在直线上有A,B,C,D四点,且AB=BC=CD.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有______个.
13.如图,点在点的北偏西80°方向上,点在点的南偏东20°的方向上,则________°.
14.如图,点O在直线AB上,OC平分,且,则______.
15.如图,某海域有三个小岛A,B,C,在小岛C处观测小岛A 在它的北偏东50°方向上,观测到小岛B在它的南偏东30°方向上,则∠ACB的度数是__________.
16.定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.如图,在的方格纸中,、在格点上,如果、在格点上,且是邻余线,那么该方格纸中符合条件的邻余四边形的个数有______个.
17.如图,在一条可以折叠的数轴上,A、B两点表示的数分别是-7,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且AB=2,则C点表示的数是______.
18.如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),给出以下结论:
①;
②;
③;
④.
其中不正确的是_________.(写出序号)
三、解答题(本大题共8个小题,共54分;第19-22每小题6分,23-24每小题7分,25-26每小题8分)
19.如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,则线段AB的长 cm;
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长;
(3)小明由(1)(2)猜想到,若点P是直线AB上的任意一点,且AB=12cm,线段MN的长与(2)中结果一样,你同意他的猜想吗?说明你的理由.
20.如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:
(1)当AC>BC时,点D在线段 上;当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)当AC<BC时,若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
21.如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
22.(1)如图,由若干个大小相同的小正方体堆砌而成的几何体,请你画出该几何体从左面、上面看到的形状图
(2)如图,已知线段,点是线段的中点,先按要求补全图形(保留痕迹).
①延长线段至点,使;延长线段至点,使;
②若点是线段的中点,求线段PB的长度.
23.直线l上的三个点A、B、C,若满足BC=AB,则称点C是点A关于点B的“半距点”.如图1,BC=AB,此时点C就是点A关于点B的一个“半距点”.
若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm.
(1)
(2)若点G也是直线m上一点,且点G是线段MP的中点,求线段GN的长度.
24.如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一块直角三角板DOE直角顶点放在点O处.
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=____________°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠BOD、∠COE的度数;
(3)如图3,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
25.多多对几何中角平分线等兴趣浓厚,请你和多多一起探究下面问题吧.已知∠AOB=100°,射线OE,OF分别是∠AOC和∠COB的角平分线.
(1)如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;
(2)如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数_____;
(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数(不写探究过程).
26.斐波那契数列是数学家莱昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13…也就是从第三个数开始,每一个数都是前两个数的和. 如图所示的长方形是由几个正方形依次拼接而成,其中最小的正方形的边长为1.
(1)如图1中最大的正方形的边长是_________.
(2)如图2所示,在小正方形中画弧,将6段圆弧依次连接起来得到曲线ABCDEFG,求曲线ABCDEFG的长.
(3)如果按此规律继续画弧,将9段圆弧依次连起来得到的曲线的长为____.
答案
一、选择题
C.C.B.B.B.C.C.D.DC.
二、填空题
11.4.
12.5.
13.120
14.105°.
15.100°.
16.6.
17.-1.
18.①③④
三、解答题
19.解:(1)∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∵MP=4cm,
∴AP=8cm,
∵P为AB的中点,
∴AB=2AP=16cm,
故答案为:16;
(2)∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴AP+BP=2MP+2PN=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm;
(3)同意.
理由:当P点在线段AB延长线上时,
∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴AP-BP=2MP-2PN=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm;
当P点在线段BA延长线上时,
∵点M、N分别是线段AP、PB的中点,
∴AP=2MP,BP=2PN,
∴BP-AP=2PN-2MP=2MN,
即AB=2MN,
∵AB=12cm,
∴MN=6cm.
20.(1)解:当AC>BC时,由“折中点”的定义可知点D在线段AC上;
当AC=BC时,点D与点C重合
当AC<BC时,点D在线段BC上
(2)
如下图,∵ E为线段AC中点
∴ AE=EC=8cm
∴ BD=AE+EC+CD=8+8+6=22(cm)
∴ CB=BD+DC=22+6=28(cm)
21.(1)∵∠NPA = 40°, ∠MPB = 30°,∠MPC = 70°,
∴∠BPC = ∠MPB + ∠MPC = 30°+70°= 100°,
∵PE平分∠BPC,
∴∠BPE =∠BPC =×100°=50°,
∴∠APB =180°-∠NPA-∠MPB = 180°-40°-30°=110°,
∴∠APE = ∠BPE + ∠APB = 50°+ 110°= 160° ,
(2)∵∠MPD = ∠BPE -∠MPB = 50°-30°= 20°,
∴轮船D在灯塔P北偏西20°的方位上 .
22.(1)如图,
(2)①如图,
②∵AM=2MN,MN=2,
∴AM=4,
∵P是AM的中点,
∴PM=AM=2,
∵,
∴BN=MN=1,
∴PB=PM+MN+BN=2+2+1=5.
23.(1)如图所示:
第一种情况:
∵ 点P是点M关于点N的“半距点”,
∴ ,
∵,
∴
第二种情况:
∵,
∴
综上:MP的长度为3cm或9cm
(2)如图所示:
第一种情况:
点是线段的中点,
∴
∴
第二种情况:
点是线段的中点,
∴
∴
综上:线段GN的长度为或.
24.(1)解:如图①,∠COE=∠DOE-∠BOC=90°-70°=20°,
故答案为:20;
(2)
如图②,∵OC平分∠EOB,∠BOC=70°,
∴∠EOB=2∠BOC=140°,
∵∠DOE=90°,
∴∠BOD=∠BOE-∠DOE=50°,
∵∠BOC=70°,
∴∠COD=∠BOC-∠BOD=20°,
∴∠COE=∠EOD-∠COD=70°;
(3)
∠COE-∠BOD=20°
理由是:如图③,∵∠BOD+∠COD=∠BOC=70°,∠COE+∠COD=∠DOE=90°,
∴(∠COE+∠COD)-(∠BOD+∠COD)
=∠COE+∠COD-∠BOD-∠COD
=∠COE-∠BOD
=90°-70°
=20°,
即∠COE-∠BOD=20°.
25.(1)
解: 是的平分线,,
,
,
,
是的平分线,
,
;
(2)
,
,
是的平分线,是的平分线,
,
故答案为:
(3)
是的平分线,是的平分线,
,
由题意,分以下三种情况:
①如图,延长至点,当射线在的内部时,
,
,
;
②如图,延长至点,延长至点,当射线在的内部时,
,
,
;
③如图,延长至点,当射线在的内部时,
,
,
;
综上,的度数为或.
26.(1)解:∵=1,
由图1知,是数列中的第六项,
∴=8,
故答案为:8;
(2)解:由图2可知,每个小正方形内的圆弧的半径都为这个小正方形的边长,
则
…
∴
∴曲线ABCDEFG的长为10π;
(3)解:根据题意得:按此规律继续画弧,将9段圆弧依次连起来得到的曲线的长为:
故答案为:44.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
