七年级数学上册试题 第五章 一元一次方程B卷-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第五章 一元一次方程B卷-北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 14:17:54 | ||
图片预览



文档简介
第五章 一元一次方程B卷
一、选择题(本大题共10个小题,每小题3分,共30分)
1.若是方程的解,则a的值是( )
A.1 B.1 C.2 D.—
2.下列方程中是一元一次方程的是( )
A. B. C. D.
3.下列根据等式的性质正确变形的是( ).
A.由,得 B.由,得
C.由,得 D.由,得
4.方程﹣3x-4=0解是( )
A.x B.x C.x D.x
5.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为x cm,可列方程( ).
A. B.
C. D.
6.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
7.今年双11狂欢节,小区超市的部分商品也搞了促销活动,一袋标价130元的大米,按照九折销售仍可获利13元,设这袋大米的成本为x元,根据题意,下面所列的方程正确的是( )
A. B.
C. D.
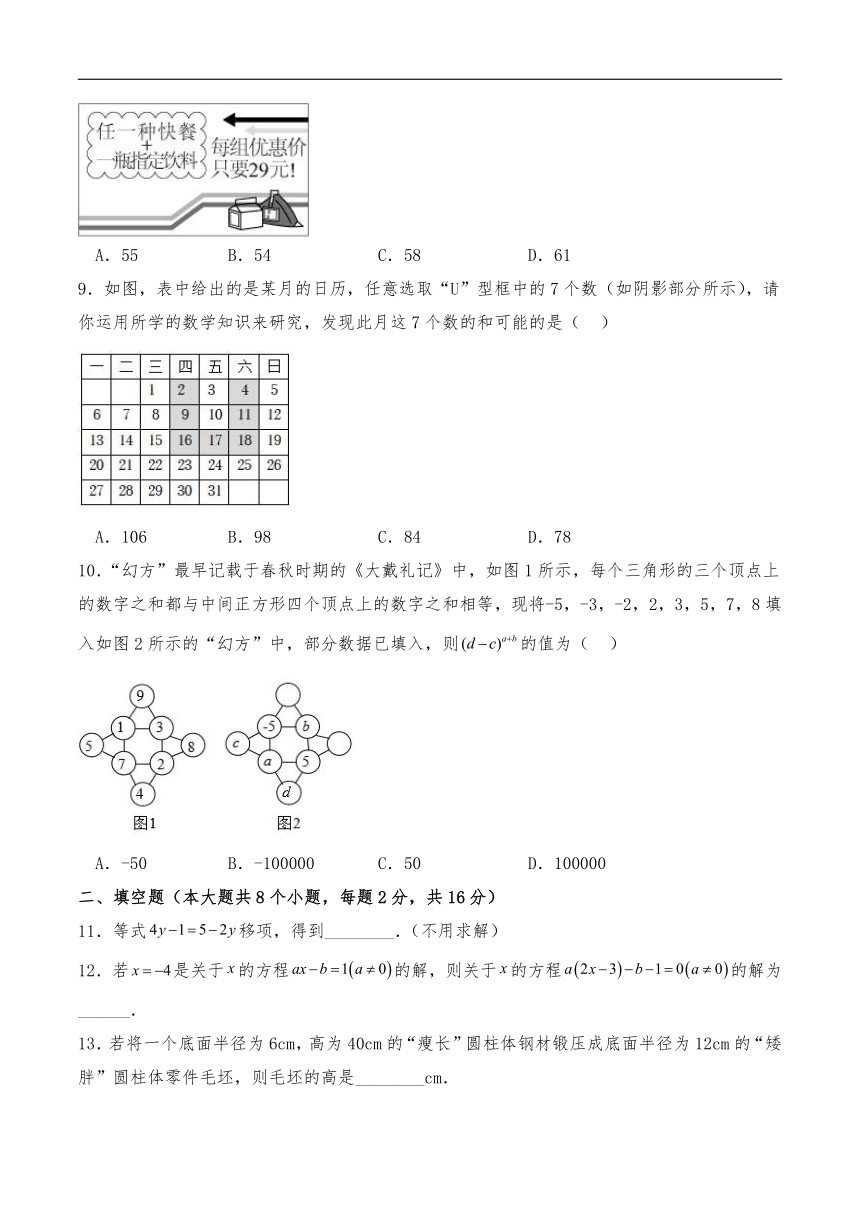
8.如图为某快餐店促销活动的内容,某同学到该快餐店购买相差6元的2种快餐各1份,结账时,店员说:“你多买2瓶指定饮料,按促销活动优惠价的金额,和你只买2份快餐的金额一样.”这位同学想了想说:“我还是只多买1瓶指定饮料吧,麻烦您以最便宜的方式给我结账,谢谢!”这位同学要付的金额是( )
A.55 B.54 C.58 D.61
9.如图,表中给出的是某月的日历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现此月这7个数的和可能的是( )
A.106 B.98 C.84 D.78
10.“幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,现将-5,-3,-2,2,3,5,7,8填入如图2所示的“幻方”中,部分数据已填入,则的值为( )
A.-50 B.-100000 C.50 D.100000
二、填空题(本大题共8个小题,每题2分,共16分)
11.等式移项,得到________.(不用求解)
12.若是关于的方程的解,则关于的方程的解为______.
13.若将一个底面半径为6cm,高为40cm的“瘦长”圆柱体钢材锻压成底面半径为12cm的“矮胖”圆柱体零件毛坯,则毛坯的高是________cm.
14.如图所示,一个单位长度表示,观察图形,回答问题:
(1)若与所表示的数互为相反数,则点所表示的数字为________.
(2)若与所表示的数互为相反数,则点所表示的数字的相反数为_______.
15.某学校组织秋游,原计划用45座的客车若干辆,则5人没有座位;如果用同样数量的50座客车,则多出一辆,且其余全部坐满.参加秋游的学生一共有 _____名.
16.某商店老板销售一种商品,他要以不低于进价20%的利润才能出售,但为了获得更多的利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,商店老板让价的最大限度为___________.
17.22年冬奥会开幕式上,烟台莱州武校的健儿们参演的立春节目让全世界人民惊艳和动容,小明想知道这震撼人心的队伍的总人数.张老师说你可以自己算算:若调配55座大巴若干辆接送他们,则有8人没有座位;若调配44座大巴接送,则用车数量将增加两辆,并空出3个座位,你能帮小明算出一共去了_______名健儿参演节目吗?
18.把1~9这九个数填入方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为______.
三、解答题(本大题共8个小题,共54分;第19-22每小题6分,23-24每小题7分,25-26每小题8分)
19.计算
(1) (2)
(3) (4)
20.已知关于x的整式,整式,若a是常数,且的值与x无关.
(1)求a的值;
(2)若b为整数,关于x的一元一次方程的解是正整数,求的值.
21.有一条围成梯形的篱笆,它的边长如图所示.因为另有他用,计划将它的形状改为一个正方形或者长是宽的倍的长方形,如果使围出的篱笆面积较大,应采用哪种围法?
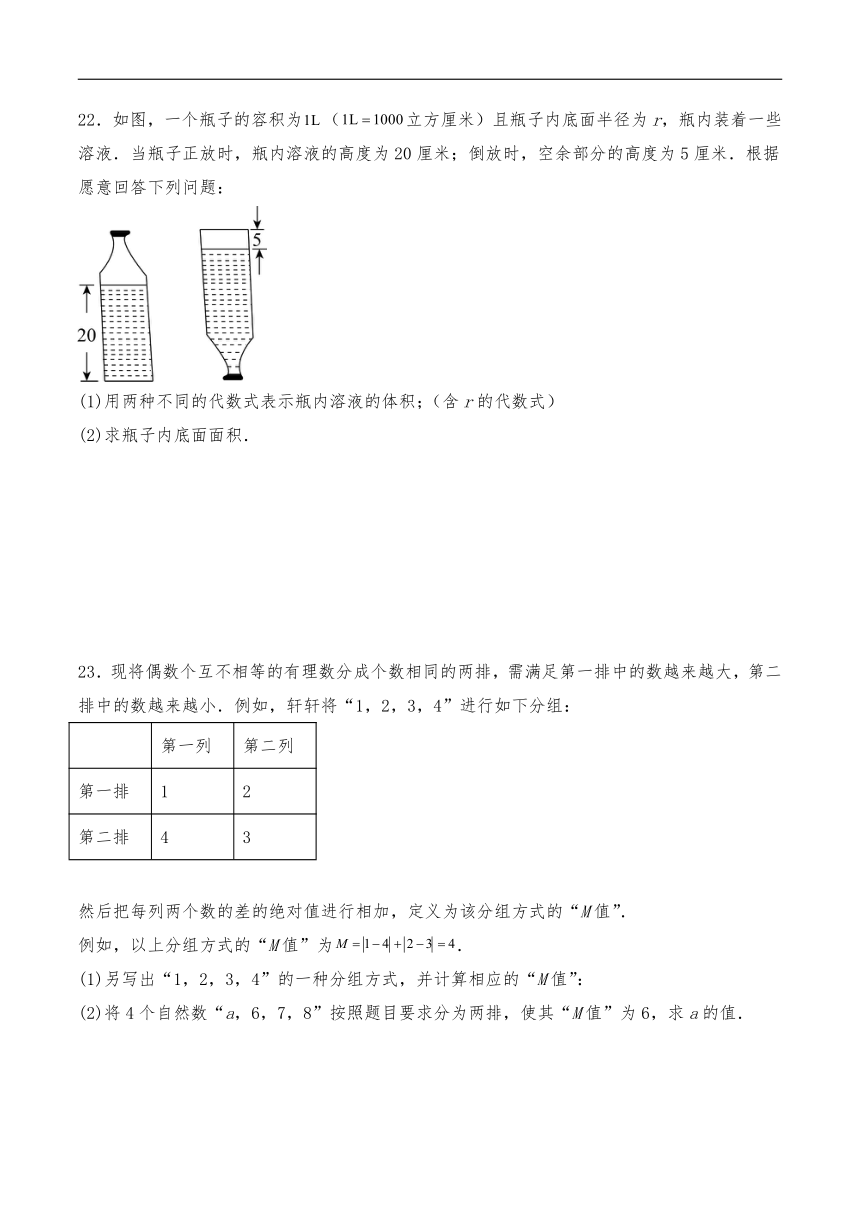
22.如图,一个瓶子的容积为(立方厘米)且瓶子内底面半径为r,瓶内装着一些溶液.当瓶子正放时,瓶内溶液的高度为20厘米;倒放时,空余部分的高度为5厘米.根据愿意回答下列问题:
(1)用两种不同的代数式表示瓶内溶液的体积;(含r的代数式)
(2)求瓶子内底面面积.
23.现将偶数个互不相等的有理数分成个数相同的两排,需满足第一排中的数越来越大,第二排中的数越来越小.例如,轩轩将“1,2,3,4”进行如下分组:
第一列 第二列
第一排 1 2
第二排 4 3
然后把每列两个数的差的绝对值进行相加,定义为该分组方式的“M值”.
例如,以上分组方式的“M值”为.
(1)另写出“1,2,3,4”的一种分组方式,并计算相应的“M值”:
(2)将4个自然数“a,6,7,8”按照题目要求分为两排,使其“M值”为6,求a的值.
24.“双11”天猫商城推出各种优惠活动进行促销.今年,张阿姨在“双11”到来之前准备在两家天猫店铺中选择一家购买原价均为1000元/条的被子若干条,店铺在活动期间分别给予以下优惠:
A店铺:“双11”当天购买可以享受8折优惠;
B店铺:商品每满1000元可使用店铺优惠券80元. 同时每满500元可使用商城双11购物津贴券50元,同时“双11”当天购买还可立减100元.(例如:购买2条被子需支付
元).
(1)若张阿姨想在“双11”当天购买4条被子,她选择哪家店铺购买 请说明理由;
(2)若张阿姨在“双11”当天购买a条被子,请分别用含a的代数式表示在这两家店铺购买的费用;
(3)张阿姨在双11当天购买几条被子,两家店铺的费用相同
25.丹尼斯经销甲、乙两种商品,甲种商品每件售价60元,利润20元;乙种商品每件进价50元,售价80元.
打折前一次性购物总金额 优惠措施
少于等于450元 不优惠
超过450元但不超过600元 按售价打九折
超过600元 其中600元部分八点二折优惠,超过600元的部分打三折优惠
(1)甲种商品每件进价为 元,每件乙种商品利润率为 ;
(2)丹尼斯同时购进甲、乙两种商品共50件,总进价为2100元,求购进甲种商品多少件?
(3)在“春节”期间,该商场对所有商品进行如下的优患促销话动:
按上述优惠条件,若小丽一次性购买乙种商品实际付款504元,求小丽购买商品的原价是多少?
26.已知在数轴上点M、N表示的数分别为a,b,点M、N两点之间的距离表示为或,记为.如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.点P是数轴上任意一点,
(1)数轴上点B表示的数是 ;
(2)如果点P到点A、点B的距离相等,那么点P表示的数是 ;
(3)若点P到点A、点B的距离之和等于14,则点P表示的数为 ;
(4)若点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动.动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,运动时间为t.求:
①当秒时P,Q两点间的距离为 ;
②当点P运动多少秒时,点P与点Q相遇?
③当点P与点Q间的距离为8个单位长度时t的值为 .
答案
一、选择题
A.A.B.A.D.C.A.A.CB.
二、填空题
11..
12..
13..
14.(1)2.5;(2)-2.
15.500.
16.120元.
17.393.
18.2.
三、解答题
19.(1)解:
;
(2)
;
(3)
移项:
合并同类项:
系数化为1:
(4)
去分母:
移项:
合并同类项:
系数化为1:
20.(1)解:∵,,
∵的值与x无关,
∴,
解得:;
(2)解:方程,
整理得:,
∵解是正整数,
∴或3,
当时,;
当时,.
∴的值为1或3.
21.解:当篱笆围成正方形时,正方形的边长为,
所以正方形的面积为
.
当篱笆围成长方形时,设长方形的宽为,则长为.
根据题意,得.
解得.
所以.
所以长方形的面积为.
因为,所以,如果使围出的篱笆面积较大,应围成正方形.
22.(1)解:根据题意知,瓶内溶液的体积=20πr2或瓶内溶液的体积=1000﹣5πr2;
(2)解:根据题意,得20πr2=1000﹣5πr2.
解得πr2=40.
答:瓶子内底面积为40cm2.
23.(1)将“1,2,3,4”进行如下分组:
第一列 第二列
第一排 1 3
第二排 4 2
∴以上分组方式的“M值”为:;
(2)①当时,
将4个自然数“a,6,7,8”按照题目要求进行如下分组:
第一列 第二列
第一排 a 6
第二排 8 7
∵以上分组方式的“M值”为6,
∴.
∴;
②当时,
将4个自然数“a,6,7,8”按照题目要求进行如下分组:
第一列 第二列
第一排 6 7
第二排 a 8
∵以上分组方式的“M值”为6,
∴.
∴;
综上,或11.
24.(1)解:由题意得,去A店铺需付款:元,
去B店铺需付款:元,
∵,
∴她选择B店铺购买;
(2)解:由题意得,去A店铺需付款:元,
去B店铺需付款:元;
(3)解:由题意得,
解得,
答:张阿姨在双11当天购买5条被子,两家店铺的费用相同.
25.(1)解:由题意得:甲种商品每件进价为;
乙种商品的利润率为,
故答案为:40,60%;
(2)解:设购进甲种商品x件,则购进乙种商品件,
由题意得:,
解得:,
答:购进甲种商品40件;
(3)解:设小丽购买商品的原价是y元,
①若小丽购买商品的原价超过450元,但不超过600元,
由题意得:,解得:,
②若小丽购买商品的原价超过600元,
由题意得:,
解得:,
答:小丽购买商品的原价是560元或640元.
26.(1)解:由题意得,
所以点B表示的数是,
故答案为:;
(2)解:设点P表示的数是x,
根据题意得,
解得,
所以点P表示的数是1,
故答案为:1;
(3)解:设点P表示的数为m,
若点P在点A与点B之间,则,不符合题意;
若点P在点B的左侧,则,
解得;
若点P在点A的右侧,则,
解得,
所以点P表示的数为或8,
故答案为:或8;
(4)解:根据题意可知,点P表示的数是,点Q表示的数是,
①当时,,,
所以,
故答案为:8;
②根据题意得,
解得,
答:当点P运动5秒时,点P与点Q相遇;
③当点P在点Q右侧时,则,
解得;
当点P在点Q左侧时,则,
解得,
综上所述,t的值为1或9,
故答案为:1或9.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.若是方程的解,则a的值是( )
A.1 B.1 C.2 D.—
2.下列方程中是一元一次方程的是( )
A. B. C. D.
3.下列根据等式的性质正确变形的是( ).
A.由,得 B.由,得
C.由,得 D.由,得
4.方程﹣3x-4=0解是( )
A.x B.x C.x D.x
5.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为x cm,可列方程( ).
A. B.
C. D.
6.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
7.今年双11狂欢节,小区超市的部分商品也搞了促销活动,一袋标价130元的大米,按照九折销售仍可获利13元,设这袋大米的成本为x元,根据题意,下面所列的方程正确的是( )
A. B.
C. D.
8.如图为某快餐店促销活动的内容,某同学到该快餐店购买相差6元的2种快餐各1份,结账时,店员说:“你多买2瓶指定饮料,按促销活动优惠价的金额,和你只买2份快餐的金额一样.”这位同学想了想说:“我还是只多买1瓶指定饮料吧,麻烦您以最便宜的方式给我结账,谢谢!”这位同学要付的金额是( )
A.55 B.54 C.58 D.61
9.如图,表中给出的是某月的日历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现此月这7个数的和可能的是( )
A.106 B.98 C.84 D.78
10.“幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,现将-5,-3,-2,2,3,5,7,8填入如图2所示的“幻方”中,部分数据已填入,则的值为( )
A.-50 B.-100000 C.50 D.100000
二、填空题(本大题共8个小题,每题2分,共16分)
11.等式移项,得到________.(不用求解)
12.若是关于的方程的解,则关于的方程的解为______.
13.若将一个底面半径为6cm,高为40cm的“瘦长”圆柱体钢材锻压成底面半径为12cm的“矮胖”圆柱体零件毛坯,则毛坯的高是________cm.
14.如图所示,一个单位长度表示,观察图形,回答问题:
(1)若与所表示的数互为相反数,则点所表示的数字为________.
(2)若与所表示的数互为相反数,则点所表示的数字的相反数为_______.
15.某学校组织秋游,原计划用45座的客车若干辆,则5人没有座位;如果用同样数量的50座客车,则多出一辆,且其余全部坐满.参加秋游的学生一共有 _____名.
16.某商店老板销售一种商品,他要以不低于进价20%的利润才能出售,但为了获得更多的利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,商店老板让价的最大限度为___________.
17.22年冬奥会开幕式上,烟台莱州武校的健儿们参演的立春节目让全世界人民惊艳和动容,小明想知道这震撼人心的队伍的总人数.张老师说你可以自己算算:若调配55座大巴若干辆接送他们,则有8人没有座位;若调配44座大巴接送,则用车数量将增加两辆,并空出3个座位,你能帮小明算出一共去了_______名健儿参演节目吗?
18.把1~9这九个数填入方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为______.
三、解答题(本大题共8个小题,共54分;第19-22每小题6分,23-24每小题7分,25-26每小题8分)
19.计算
(1) (2)
(3) (4)
20.已知关于x的整式,整式,若a是常数,且的值与x无关.
(1)求a的值;
(2)若b为整数,关于x的一元一次方程的解是正整数,求的值.
21.有一条围成梯形的篱笆,它的边长如图所示.因为另有他用,计划将它的形状改为一个正方形或者长是宽的倍的长方形,如果使围出的篱笆面积较大,应采用哪种围法?
22.如图,一个瓶子的容积为(立方厘米)且瓶子内底面半径为r,瓶内装着一些溶液.当瓶子正放时,瓶内溶液的高度为20厘米;倒放时,空余部分的高度为5厘米.根据愿意回答下列问题:
(1)用两种不同的代数式表示瓶内溶液的体积;(含r的代数式)
(2)求瓶子内底面面积.
23.现将偶数个互不相等的有理数分成个数相同的两排,需满足第一排中的数越来越大,第二排中的数越来越小.例如,轩轩将“1,2,3,4”进行如下分组:
第一列 第二列
第一排 1 2
第二排 4 3
然后把每列两个数的差的绝对值进行相加,定义为该分组方式的“M值”.
例如,以上分组方式的“M值”为.
(1)另写出“1,2,3,4”的一种分组方式,并计算相应的“M值”:
(2)将4个自然数“a,6,7,8”按照题目要求分为两排,使其“M值”为6,求a的值.
24.“双11”天猫商城推出各种优惠活动进行促销.今年,张阿姨在“双11”到来之前准备在两家天猫店铺中选择一家购买原价均为1000元/条的被子若干条,店铺在活动期间分别给予以下优惠:
A店铺:“双11”当天购买可以享受8折优惠;
B店铺:商品每满1000元可使用店铺优惠券80元. 同时每满500元可使用商城双11购物津贴券50元,同时“双11”当天购买还可立减100元.(例如:购买2条被子需支付
元).
(1)若张阿姨想在“双11”当天购买4条被子,她选择哪家店铺购买 请说明理由;
(2)若张阿姨在“双11”当天购买a条被子,请分别用含a的代数式表示在这两家店铺购买的费用;
(3)张阿姨在双11当天购买几条被子,两家店铺的费用相同
25.丹尼斯经销甲、乙两种商品,甲种商品每件售价60元,利润20元;乙种商品每件进价50元,售价80元.
打折前一次性购物总金额 优惠措施
少于等于450元 不优惠
超过450元但不超过600元 按售价打九折
超过600元 其中600元部分八点二折优惠,超过600元的部分打三折优惠
(1)甲种商品每件进价为 元,每件乙种商品利润率为 ;
(2)丹尼斯同时购进甲、乙两种商品共50件,总进价为2100元,求购进甲种商品多少件?
(3)在“春节”期间,该商场对所有商品进行如下的优患促销话动:
按上述优惠条件,若小丽一次性购买乙种商品实际付款504元,求小丽购买商品的原价是多少?
26.已知在数轴上点M、N表示的数分别为a,b,点M、N两点之间的距离表示为或,记为.如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.点P是数轴上任意一点,
(1)数轴上点B表示的数是 ;
(2)如果点P到点A、点B的距离相等,那么点P表示的数是 ;
(3)若点P到点A、点B的距离之和等于14,则点P表示的数为 ;
(4)若点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动.动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,运动时间为t.求:
①当秒时P,Q两点间的距离为 ;
②当点P运动多少秒时,点P与点Q相遇?
③当点P与点Q间的距离为8个单位长度时t的值为 .
答案
一、选择题
A.A.B.A.D.C.A.A.CB.
二、填空题
11..
12..
13..
14.(1)2.5;(2)-2.
15.500.
16.120元.
17.393.
18.2.
三、解答题
19.(1)解:
;
(2)
;
(3)
移项:
合并同类项:
系数化为1:
(4)
去分母:
移项:
合并同类项:
系数化为1:
20.(1)解:∵,,
∵的值与x无关,
∴,
解得:;
(2)解:方程,
整理得:,
∵解是正整数,
∴或3,
当时,;
当时,.
∴的值为1或3.
21.解:当篱笆围成正方形时,正方形的边长为,
所以正方形的面积为
.
当篱笆围成长方形时,设长方形的宽为,则长为.
根据题意,得.
解得.
所以.
所以长方形的面积为.
因为,所以,如果使围出的篱笆面积较大,应围成正方形.
22.(1)解:根据题意知,瓶内溶液的体积=20πr2或瓶内溶液的体积=1000﹣5πr2;
(2)解:根据题意,得20πr2=1000﹣5πr2.
解得πr2=40.
答:瓶子内底面积为40cm2.
23.(1)将“1,2,3,4”进行如下分组:
第一列 第二列
第一排 1 3
第二排 4 2
∴以上分组方式的“M值”为:;
(2)①当时,
将4个自然数“a,6,7,8”按照题目要求进行如下分组:
第一列 第二列
第一排 a 6
第二排 8 7
∵以上分组方式的“M值”为6,
∴.
∴;
②当时,
将4个自然数“a,6,7,8”按照题目要求进行如下分组:
第一列 第二列
第一排 6 7
第二排 a 8
∵以上分组方式的“M值”为6,
∴.
∴;
综上,或11.
24.(1)解:由题意得,去A店铺需付款:元,
去B店铺需付款:元,
∵,
∴她选择B店铺购买;
(2)解:由题意得,去A店铺需付款:元,
去B店铺需付款:元;
(3)解:由题意得,
解得,
答:张阿姨在双11当天购买5条被子,两家店铺的费用相同.
25.(1)解:由题意得:甲种商品每件进价为;
乙种商品的利润率为,
故答案为:40,60%;
(2)解:设购进甲种商品x件,则购进乙种商品件,
由题意得:,
解得:,
答:购进甲种商品40件;
(3)解:设小丽购买商品的原价是y元,
①若小丽购买商品的原价超过450元,但不超过600元,
由题意得:,解得:,
②若小丽购买商品的原价超过600元,
由题意得:,
解得:,
答:小丽购买商品的原价是560元或640元.
26.(1)解:由题意得,
所以点B表示的数是,
故答案为:;
(2)解:设点P表示的数是x,
根据题意得,
解得,
所以点P表示的数是1,
故答案为:1;
(3)解:设点P表示的数为m,
若点P在点A与点B之间,则,不符合题意;
若点P在点B的左侧,则,
解得;
若点P在点A的右侧,则,
解得,
所以点P表示的数为或8,
故答案为:或8;
(4)解:根据题意可知,点P表示的数是,点Q表示的数是,
①当时,,,
所以,
故答案为:8;
②根据题意得,
解得,
答:当点P运动5秒时,点P与点Q相遇;
③当点P在点Q右侧时,则,
解得;
当点P在点Q左侧时,则,
解得,
综上所述,t的值为1或9,
故答案为:1或9.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
