3.2解一元一次方程(一)——合并同类项与移项第2课时课件
文档属性
| 名称 | 3.2解一元一次方程(一)——合并同类项与移项第2课时课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 00:00:00 | ||
图片预览









文档简介
课件31张PPT。3.2 解一元一次方程(一)
——合并同类项与移项
第2课时1.进一步认识解方程的基本变形——移项,感悟解方程过程中的转化思想.(重点)
2.会用移项、合并同类项解ax+b=cx+d型的方程.(重点)
3.能通过分析问题找到相等关系并通过列方程解决问题.(重点、难点)用移项解一元一次方程
3x-20=4x-25
移项将含有未知数的项移到方程
的左边,常数项移到方程的右边
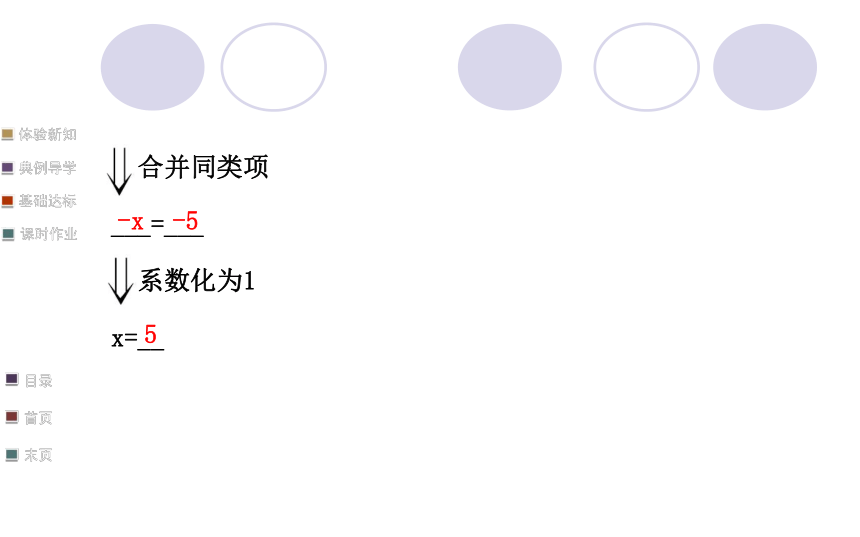
3x+______=-25+___(-4x)20 合并同类项
___=___
?系数化为1
x=__-x-55【归纳】解“ax+b=cx+d”型的一元一次方程的步骤:
(1)_____.(2)___________.(3)系数化为1.移项合并同类项 (打“√”或“×”)
(1)方程5x-2=6移项,得5x=6-2.( )
(2)方程 移项,得 ( )
(3)方程32-2x=28+6x移项,得32-28=6x+2x.( )
(4)方程7x-8=13+x移项,得7x-x=-13+8.( )×√√×知识点 1 用移项解一元一次方程
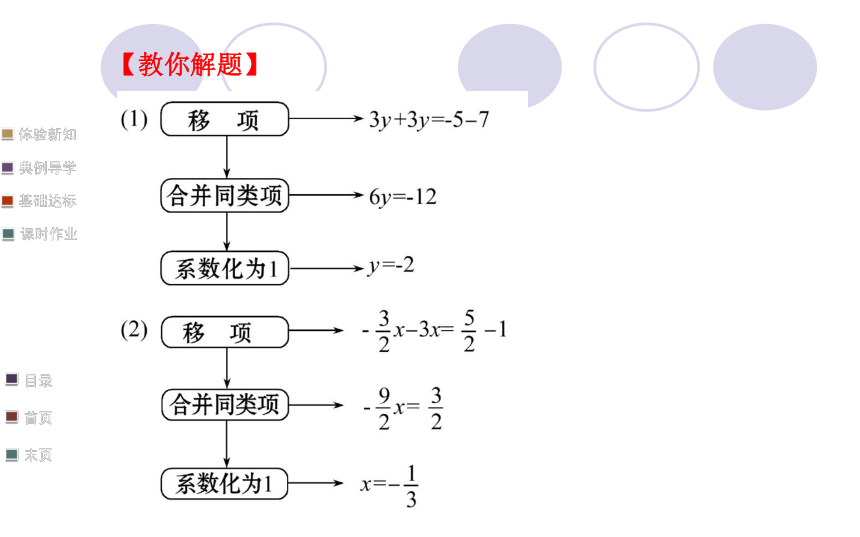
【例1】解方程:(1)3y+7=-3y-5.
(2) 【教你解题】【总结提升】“移项”的正确理解
1.实质:等式的性质1的应用.
2.特点:某项从一边移到另一边,要改变它的系数符号.
3.目的:把含未知数的项通常放在等号的左边,将含未知数的项合并;常数项通常放在等号的右边,将常数项合并,最终化成形如“x=a”的形式.
4.注意:移项必变号,不移动的项不变号.知识点 2 解一元一次方程的应用题
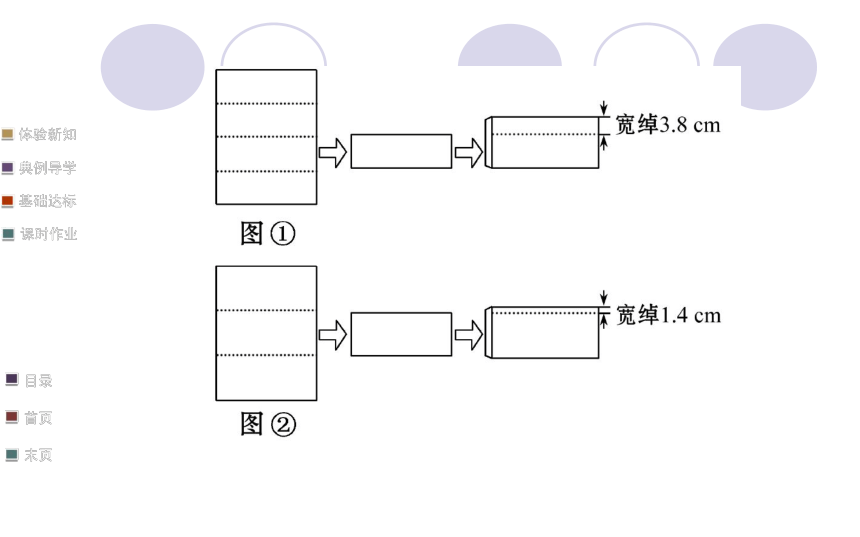
【例2】(2012·江西中考)小华写信给老家的爷爷,问候“八一”建军节.折叠长方形信纸、装入标准信封时发现:若将信纸如图①连续两次对折后,沿着信封口边线装入时,宽绰有3.8 cm;若将信纸如图②三等分折叠后,同样方法装入时,宽绰1.4 cm.试求信纸的纸长与信封的口宽.【思路点拨】设信纸长x cm 用x分别表示两种方式折叠后
的信纸宽 相等关系:信封口宽不变→列方程【自主解答】设信纸的纸长为x cm,
根据题意,得
移项,得
合并同类项,得
解得x=28.8,
所以信封的口宽为
答:信纸的纸长为28.8 cm,信封的口宽为11 cm.【总结提升】解决“表示同一个量的两个不同式子相等”应用题的四个步骤
1.找出能贯穿应用题始终的一个不变的量.
2.用两个不同的式子去表示这个量.
3.由表示这个不变的量的两个式子相等列出方程.
4.解方程并作答.题组一:用移项解一元一次方程
1.解方程6x+1=-4,移项正确的是( )
A.6x=4-1 B.-6x=-4-1
C.6x=1-4 D.6x=-4-1
【解析】选D.选项A,B的错误是没移动的项符号发生了改变;选项C中的1从左移到右,而符号没改变.2.下列方程变形正确的是( )
A.由-2x=6, 得x=3
B.由-3=x+2, 得x=-3-2
C.由-7x+3=x-3, 得(-7+1)x=-3-3
D.由5x=2x+3, 得x=-1
【解析】选B.把2从右边移到左边,得-3-2=x,所以x=-3-2.3.(2012·泉州中考)方程x-5=0的解是________.
【解析】移项,得x=5.
答案:x=54.(2012·郴州中考)一元一次方程3x-6=0的解是_______.
【解析】移项,得3x=6,系数化为1,得x=2.
答案:x=2【变式训练】已知当x=2,y=1时,代数式kx-y的值是3,那么k的值是 .
【解析】由题意,得2k-1=3,
移项,得2k=3+1,
合并同类项,得2k=4,
系数化为1,得k=2.
答案:25.若5x-7与4x+9的值相等,则x=_______.
【解析】解方程5x-7=4x+9,得x=16.
答案:166.解方程:4x+5-3x=3-2x.
【解析】移项,得4x-3x+2x=3-5.
合并同类项,得3x=-2.
系数化为1,得题组二:解一元一次方程的应用题
1.我国民间流传着许多趣味算题,多以顺口溜的形式表达,请看这样一个数学问题:一群老头去赶集,半路买了一堆梨,一人一个多一个,一人两个少两个,老头和梨分别是( )
A.3个老头,4个梨 B.4个老头,3个梨
C.5个老头,6个梨 D.7个老头,8个梨
【解析】选A.设有x个老头,则x+1=2x-2,解得,x=3,所以梨有3+1=4个.2.在甲地工作的有272人,乙地工作的有196人,要使在乙地工
作的人数是甲地的 应从乙地调多少人到甲地?若设应从乙
地调x人到甲地,那么下列方程正确的是( )
【解析】选D.调动后甲地有(272+x)人,乙地有(196-x)人,相
等关系为乙地人数是甲地的3.(2012·天水中考)某商店一套西服的进价为300元,按标价的80%销售可获利100元,则该服装的标价为_____元.
【解析】设该服装的标价为x元,由题意可列方程80%x-300=100,解得x=500.
答案:5004.小文最近买了12本书,这比他原有书的 还多3本,则小文
原有书的本数是______.
【解析】设小文原有书x本,则 解得x=36.
答案:365.(2012·云南中考)某企业为严重缺水的甲、乙两所学校捐赠矿泉水共2 000件.已知捐给甲校的矿泉水件数比捐给乙校件数的2倍少400件.求该企业捐给甲、乙两所学校的矿泉水各多少件?【解析】设企业捐给乙校矿泉水x件,则捐给甲校矿泉水
(2x-400)件,
根据题意,得x+2x-400=2 000.
解方程,得x=800.
答:该企业捐给甲校矿泉水1 200件,乙校矿泉水800件.6.二班组织全班同学去郊游,但需要一定费用,如果每名同学付5元,那么还差5.6元,如果每名同学付5.5元,就多出10.4元,那么这个班有多少名同学,总开支多少元?
【解析】设有x名同学,则5x+5.6=5.5x-10.4,
所以x=32,
所以5x+5.6=5×32+5.6=165.6.
答:这个班共有32名同学,总开支165.6元.【想一想错在哪?】解方程:20x-8=32-28x.
提示:方程中的任何一项从等号的一边移到另一边都必须变号.
——合并同类项与移项
第2课时1.进一步认识解方程的基本变形——移项,感悟解方程过程中的转化思想.(重点)
2.会用移项、合并同类项解ax+b=cx+d型的方程.(重点)
3.能通过分析问题找到相等关系并通过列方程解决问题.(重点、难点)用移项解一元一次方程
3x-20=4x-25
移项将含有未知数的项移到方程
的左边,常数项移到方程的右边
3x+______=-25+___(-4x)20 合并同类项
___=___
?系数化为1
x=__-x-55【归纳】解“ax+b=cx+d”型的一元一次方程的步骤:
(1)_____.(2)___________.(3)系数化为1.移项合并同类项 (打“√”或“×”)
(1)方程5x-2=6移项,得5x=6-2.( )
(2)方程 移项,得 ( )
(3)方程32-2x=28+6x移项,得32-28=6x+2x.( )
(4)方程7x-8=13+x移项,得7x-x=-13+8.( )×√√×知识点 1 用移项解一元一次方程
【例1】解方程:(1)3y+7=-3y-5.
(2) 【教你解题】【总结提升】“移项”的正确理解
1.实质:等式的性质1的应用.
2.特点:某项从一边移到另一边,要改变它的系数符号.
3.目的:把含未知数的项通常放在等号的左边,将含未知数的项合并;常数项通常放在等号的右边,将常数项合并,最终化成形如“x=a”的形式.
4.注意:移项必变号,不移动的项不变号.知识点 2 解一元一次方程的应用题
【例2】(2012·江西中考)小华写信给老家的爷爷,问候“八一”建军节.折叠长方形信纸、装入标准信封时发现:若将信纸如图①连续两次对折后,沿着信封口边线装入时,宽绰有3.8 cm;若将信纸如图②三等分折叠后,同样方法装入时,宽绰1.4 cm.试求信纸的纸长与信封的口宽.【思路点拨】设信纸长x cm 用x分别表示两种方式折叠后
的信纸宽 相等关系:信封口宽不变→列方程【自主解答】设信纸的纸长为x cm,
根据题意,得
移项,得
合并同类项,得
解得x=28.8,
所以信封的口宽为
答:信纸的纸长为28.8 cm,信封的口宽为11 cm.【总结提升】解决“表示同一个量的两个不同式子相等”应用题的四个步骤
1.找出能贯穿应用题始终的一个不变的量.
2.用两个不同的式子去表示这个量.
3.由表示这个不变的量的两个式子相等列出方程.
4.解方程并作答.题组一:用移项解一元一次方程
1.解方程6x+1=-4,移项正确的是( )
A.6x=4-1 B.-6x=-4-1
C.6x=1-4 D.6x=-4-1
【解析】选D.选项A,B的错误是没移动的项符号发生了改变;选项C中的1从左移到右,而符号没改变.2.下列方程变形正确的是( )
A.由-2x=6, 得x=3
B.由-3=x+2, 得x=-3-2
C.由-7x+3=x-3, 得(-7+1)x=-3-3
D.由5x=2x+3, 得x=-1
【解析】选B.把2从右边移到左边,得-3-2=x,所以x=-3-2.3.(2012·泉州中考)方程x-5=0的解是________.
【解析】移项,得x=5.
答案:x=54.(2012·郴州中考)一元一次方程3x-6=0的解是_______.
【解析】移项,得3x=6,系数化为1,得x=2.
答案:x=2【变式训练】已知当x=2,y=1时,代数式kx-y的值是3,那么k的值是 .
【解析】由题意,得2k-1=3,
移项,得2k=3+1,
合并同类项,得2k=4,
系数化为1,得k=2.
答案:25.若5x-7与4x+9的值相等,则x=_______.
【解析】解方程5x-7=4x+9,得x=16.
答案:166.解方程:4x+5-3x=3-2x.
【解析】移项,得4x-3x+2x=3-5.
合并同类项,得3x=-2.
系数化为1,得题组二:解一元一次方程的应用题
1.我国民间流传着许多趣味算题,多以顺口溜的形式表达,请看这样一个数学问题:一群老头去赶集,半路买了一堆梨,一人一个多一个,一人两个少两个,老头和梨分别是( )
A.3个老头,4个梨 B.4个老头,3个梨
C.5个老头,6个梨 D.7个老头,8个梨
【解析】选A.设有x个老头,则x+1=2x-2,解得,x=3,所以梨有3+1=4个.2.在甲地工作的有272人,乙地工作的有196人,要使在乙地工
作的人数是甲地的 应从乙地调多少人到甲地?若设应从乙
地调x人到甲地,那么下列方程正确的是( )
【解析】选D.调动后甲地有(272+x)人,乙地有(196-x)人,相
等关系为乙地人数是甲地的3.(2012·天水中考)某商店一套西服的进价为300元,按标价的80%销售可获利100元,则该服装的标价为_____元.
【解析】设该服装的标价为x元,由题意可列方程80%x-300=100,解得x=500.
答案:5004.小文最近买了12本书,这比他原有书的 还多3本,则小文
原有书的本数是______.
【解析】设小文原有书x本,则 解得x=36.
答案:365.(2012·云南中考)某企业为严重缺水的甲、乙两所学校捐赠矿泉水共2 000件.已知捐给甲校的矿泉水件数比捐给乙校件数的2倍少400件.求该企业捐给甲、乙两所学校的矿泉水各多少件?【解析】设企业捐给乙校矿泉水x件,则捐给甲校矿泉水
(2x-400)件,
根据题意,得x+2x-400=2 000.
解方程,得x=800.
答:该企业捐给甲校矿泉水1 200件,乙校矿泉水800件.6.二班组织全班同学去郊游,但需要一定费用,如果每名同学付5元,那么还差5.6元,如果每名同学付5.5元,就多出10.4元,那么这个班有多少名同学,总开支多少元?
【解析】设有x名同学,则5x+5.6=5.5x-10.4,
所以x=32,
所以5x+5.6=5×32+5.6=165.6.
答:这个班共有32名同学,总开支165.6元.【想一想错在哪?】解方程:20x-8=32-28x.
提示:方程中的任何一项从等号的一边移到另一边都必须变号.
