3.3解一元一次方程(二)——去括号与去分母第2课时课件
文档属性
| 名称 | 3.3解一元一次方程(二)——去括号与去分母第2课时课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 11:01:34 | ||
图片预览











文档简介
课件30张PPT。3.3 解一元一次方程(二)
——去括号与去分母
第2课时1.会解有分数系数的一元一次方程.(重点)
2.熟悉解一元一次方程的步骤,会灵活地解一元一次方程.(重点、难点)解有分数系数的一元一次方程
【思考】1.方程 的系数有什么特点?
提示:_________.
2.根据等式的性质2,方程两边同乘什么数(非0)可使上面方
程各项系数都化为整数?并写出变形后的方程.
提示:方程两边同乘____________________,变形后的方程
为____________.都是分数各分母的最小公倍数63x+2x+66=6x3.解上面变形后的方程有哪些步骤?
提示:_____、___________、__________.
【总结】解有分数系数的一元一次方程的一般步骤有:去
____、去括号、____、合并_______、系数_______.移项合并同类项系数化为1分母移项同类项化为1 (打“√”或“×”)
(1)三个数2,3,10的最小公倍数是60.( )
(2)解方程 去分母时,两边同乘6最合适.( )
(3)方程 去分母得4(x+1)= 20x.( )
(4)方程 去分母得2(y-21)+7=10y.( )
(5)方程 去分母得15-x-2=18x.( )×√×××知识点 1 解有分数系数的一元一次方程
【例1】解方程:(1)
(2)
【思路点拨】(1)去分母→去括号→移项→合并同类项→系数
化为1.
(2)利用分数的基本性质把分母(或分子)中的小数化为整数→
去分母→去括号→移项→合并同类项→系数化为1.【自主解答】(1)去分母(方程两边同乘以12),得
3(3y+12)=24-4(5y-7),
去括号,得9y+36=24-20y+28,
移项,得9y+20y=24+28-36,
合并同类项,得29y=16,
系数化为1,得(2)原方程可化为
去分母(方程两边同乘以6),
得20x-3(17-20x)=6,
去括号,得20x-51+60x=6,
移项,得20x+60x=6+51,
合并同类项,得80x=57,
系数化为1,得【总结提升】解方程时去分母的四点注意
方程中含有分数系数,解方程时,一般先去分母,再做其他变形.去分母时应注意:
1.所选的乘数是方程中所有分母的最小公倍数,不要遗漏某个分母.2.用各分母的最小公倍数乘方程的两边时,不要遗漏方程中不含分母的项.
3.去掉分母后,分数线也同时去掉,分子上的多项式要用括号括起来(分数线有括号的作用).
4.若分子或分母中有小数时,一般先用分数的基本性质把分子或分母中的小数化为整数,再去分母.知识点 2 有分数系数的一元一次方程应用题
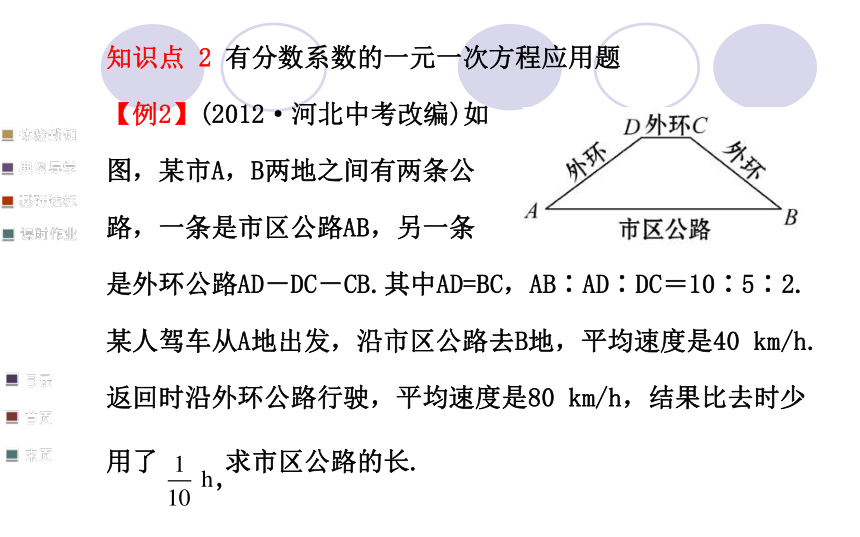
【例2】(2012·河北中考改编)如
图,某市A,B两地之间有两条公
路,一条是市区公路AB,另一条
是外环公路AD-DC-CB.其中AD=BC,AB∶AD∶DC=10∶5∶2.
某人驾车从A地出发,沿市区公路去B地,平均速度是40 km/h.
返回时沿外环公路行驶,平均速度是80 km/h,结果比去时少
用了 求市区公路的长.【解题探究】1.由AB∶AD∶DC=10∶5∶2,若设AB的长为
10x km,应如何用未知数表示出AD和DC.
提示:AD=5x km,DC=2x km.
2.本题中的相等关系是什么?
提示:返回时比去时少用了 即去时所用时间-返回时间3.去时所用的时间为多少?返回时所用的时间又是多少?
提示:去时所用的时间为 返回时所用的时间为
4.根据2,3可列出方程为 .
5.解4中所列的方程可得____.
6.市区公路的长为_________(km).x=110×1=10【总结提升】行程问题中的三个重要量
路程、速度、时间是行程问题中的三个重要量.其中一个量在问题中是已知的(如例题中的速度);一个量是未知的(如例题中的路程),一般设这个量为x;问题还涉及一个量在不同过程中的关系(如例题中的时间),常常把这个关系作为列方程的相等关系.题组一:解有分数系数的一元一次方程
1.方程 去分母正确的是( )
A.2x=1-(x-1) B.2x=4-x-1
C.2x=4-(x-1) D.4x=4-2(x-1)
【解析】选C.选项A中的1漏乘了4;选项B中的x-1应加括号;
选项D是由 乘8,1乘4得到的,方程两边每一项乘的
数不同.2.解方程 去分母时,两边同乘以( )
A.72 B.36 C.18 D.12
【解析】选C.去分母时,方程两边同乘各分母的最小公倍数,
故需乘18.3.当x=_______时,
【解析】去分母,得2x-1=3x,移项,得2x-3x=1,
合并同类项,得-x=1.系数化为1,得x=-1.
答案:-14.若2(a-6)与 互为相反数,则a=_______.
【解析】由题意, 去分母,得:4(a-6)+a-
1=0;去括号,得4a-24+a-1=0;移项,得4a+a=24+1,合并同
类项,得5a=25,系数化为1,得a=5.
答案:55.解方程:
【解析】(1)去分母,得x+8=-3x,
移项,得x+3x=-8,
合并同类项,得4x=-8,
系数化为1,得x=-2.
(2)去分母,得2(2x-1)=3(x+2)+6,
去括号,得4x-2=3x+6+6,
移项,得4x-3x=6+6+2,
合并同类项,得x=14.【归纳整合】解一元一次方程的步骤
(1)去分母.(2)去括号.(3)移项.(4)合并同类项.(5)系数化为1.但并不是解每一个方程都需要这五个步骤,这五个步骤的先后顺序并非固定不变,要根据方程的特点,确定恰当的步骤,灵活解方程.题组二:有分数系数的一元一次方程应用题
1.小方读了一本故事书,第一天读了全书的 第二天读了剩
下的 这时还有24页没有读,则他第二天读的页数为( )
A.12 B.18 C.24 D.36
【解析】选A.设全书有x页,则 即
去分母得3x+2x+216=9x,移项、合并同类项
得-4x=-216,系数化为1,得x=54,所以2.根据以下对话(如图),可以求得小红所买的笔和笔记本的价格分别是( )
A.0.8元/支,2.6元/本 B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本【解析】选D.设一支笔的价格为x元,
则一本笔记本的价格为 元,
由已知条件可得
所以x=1.2,
所以3.一批货物用载重1.5吨的汽车运送,比用载重4吨的大卡车运
送要多运5次才能运完,设这批货物x吨,则可列方程为____.
【解析】用载重1.5吨的汽车运送需 次,用载重4吨的大卡
车运送需 次,所以
答案:4.抄写一篇文章,每分钟可抄30个字,当抄了 的时候,抄写
速度提高到每分钟45个字,结果提前20分钟抄完,求这篇文章
的字数.
【解析】设这篇文章的 有x个字,则
解得x=1 800,所以
答:这篇文章的字数为3 000字.【一题多解】设这篇文章有x个字,则 方程变形
为 解得x=3 000.
答:这篇文章的字数为3 000字.5.七年级一班全体学生参加课外活动,原来每组8人;后来根
据需要重新编组,比原来少了3组,每组14人.求这个班的人数.
【解析】设这个班共有学生x人,则
解得x=56.
答:这个班共有56人.【想一想错在哪?】解方程:
提示:去分母时,不能漏乘不含分母的项,分子是多项式的要
加括号.
——去括号与去分母
第2课时1.会解有分数系数的一元一次方程.(重点)
2.熟悉解一元一次方程的步骤,会灵活地解一元一次方程.(重点、难点)解有分数系数的一元一次方程
【思考】1.方程 的系数有什么特点?
提示:_________.
2.根据等式的性质2,方程两边同乘什么数(非0)可使上面方
程各项系数都化为整数?并写出变形后的方程.
提示:方程两边同乘____________________,变形后的方程
为____________.都是分数各分母的最小公倍数63x+2x+66=6x3.解上面变形后的方程有哪些步骤?
提示:_____、___________、__________.
【总结】解有分数系数的一元一次方程的一般步骤有:去
____、去括号、____、合并_______、系数_______.移项合并同类项系数化为1分母移项同类项化为1 (打“√”或“×”)
(1)三个数2,3,10的最小公倍数是60.( )
(2)解方程 去分母时,两边同乘6最合适.( )
(3)方程 去分母得4(x+1)= 20x.( )
(4)方程 去分母得2(y-21)+7=10y.( )
(5)方程 去分母得15-x-2=18x.( )×√×××知识点 1 解有分数系数的一元一次方程
【例1】解方程:(1)
(2)
【思路点拨】(1)去分母→去括号→移项→合并同类项→系数
化为1.
(2)利用分数的基本性质把分母(或分子)中的小数化为整数→
去分母→去括号→移项→合并同类项→系数化为1.【自主解答】(1)去分母(方程两边同乘以12),得
3(3y+12)=24-4(5y-7),
去括号,得9y+36=24-20y+28,
移项,得9y+20y=24+28-36,
合并同类项,得29y=16,
系数化为1,得(2)原方程可化为
去分母(方程两边同乘以6),
得20x-3(17-20x)=6,
去括号,得20x-51+60x=6,
移项,得20x+60x=6+51,
合并同类项,得80x=57,
系数化为1,得【总结提升】解方程时去分母的四点注意
方程中含有分数系数,解方程时,一般先去分母,再做其他变形.去分母时应注意:
1.所选的乘数是方程中所有分母的最小公倍数,不要遗漏某个分母.2.用各分母的最小公倍数乘方程的两边时,不要遗漏方程中不含分母的项.
3.去掉分母后,分数线也同时去掉,分子上的多项式要用括号括起来(分数线有括号的作用).
4.若分子或分母中有小数时,一般先用分数的基本性质把分子或分母中的小数化为整数,再去分母.知识点 2 有分数系数的一元一次方程应用题
【例2】(2012·河北中考改编)如
图,某市A,B两地之间有两条公
路,一条是市区公路AB,另一条
是外环公路AD-DC-CB.其中AD=BC,AB∶AD∶DC=10∶5∶2.
某人驾车从A地出发,沿市区公路去B地,平均速度是40 km/h.
返回时沿外环公路行驶,平均速度是80 km/h,结果比去时少
用了 求市区公路的长.【解题探究】1.由AB∶AD∶DC=10∶5∶2,若设AB的长为
10x km,应如何用未知数表示出AD和DC.
提示:AD=5x km,DC=2x km.
2.本题中的相等关系是什么?
提示:返回时比去时少用了 即去时所用时间-返回时间3.去时所用的时间为多少?返回时所用的时间又是多少?
提示:去时所用的时间为 返回时所用的时间为
4.根据2,3可列出方程为 .
5.解4中所列的方程可得____.
6.市区公路的长为_________(km).x=110×1=10【总结提升】行程问题中的三个重要量
路程、速度、时间是行程问题中的三个重要量.其中一个量在问题中是已知的(如例题中的速度);一个量是未知的(如例题中的路程),一般设这个量为x;问题还涉及一个量在不同过程中的关系(如例题中的时间),常常把这个关系作为列方程的相等关系.题组一:解有分数系数的一元一次方程
1.方程 去分母正确的是( )
A.2x=1-(x-1) B.2x=4-x-1
C.2x=4-(x-1) D.4x=4-2(x-1)
【解析】选C.选项A中的1漏乘了4;选项B中的x-1应加括号;
选项D是由 乘8,1乘4得到的,方程两边每一项乘的
数不同.2.解方程 去分母时,两边同乘以( )
A.72 B.36 C.18 D.12
【解析】选C.去分母时,方程两边同乘各分母的最小公倍数,
故需乘18.3.当x=_______时,
【解析】去分母,得2x-1=3x,移项,得2x-3x=1,
合并同类项,得-x=1.系数化为1,得x=-1.
答案:-14.若2(a-6)与 互为相反数,则a=_______.
【解析】由题意, 去分母,得:4(a-6)+a-
1=0;去括号,得4a-24+a-1=0;移项,得4a+a=24+1,合并同
类项,得5a=25,系数化为1,得a=5.
答案:55.解方程:
【解析】(1)去分母,得x+8=-3x,
移项,得x+3x=-8,
合并同类项,得4x=-8,
系数化为1,得x=-2.
(2)去分母,得2(2x-1)=3(x+2)+6,
去括号,得4x-2=3x+6+6,
移项,得4x-3x=6+6+2,
合并同类项,得x=14.【归纳整合】解一元一次方程的步骤
(1)去分母.(2)去括号.(3)移项.(4)合并同类项.(5)系数化为1.但并不是解每一个方程都需要这五个步骤,这五个步骤的先后顺序并非固定不变,要根据方程的特点,确定恰当的步骤,灵活解方程.题组二:有分数系数的一元一次方程应用题
1.小方读了一本故事书,第一天读了全书的 第二天读了剩
下的 这时还有24页没有读,则他第二天读的页数为( )
A.12 B.18 C.24 D.36
【解析】选A.设全书有x页,则 即
去分母得3x+2x+216=9x,移项、合并同类项
得-4x=-216,系数化为1,得x=54,所以2.根据以下对话(如图),可以求得小红所买的笔和笔记本的价格分别是( )
A.0.8元/支,2.6元/本 B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本【解析】选D.设一支笔的价格为x元,
则一本笔记本的价格为 元,
由已知条件可得
所以x=1.2,
所以3.一批货物用载重1.5吨的汽车运送,比用载重4吨的大卡车运
送要多运5次才能运完,设这批货物x吨,则可列方程为____.
【解析】用载重1.5吨的汽车运送需 次,用载重4吨的大卡
车运送需 次,所以
答案:4.抄写一篇文章,每分钟可抄30个字,当抄了 的时候,抄写
速度提高到每分钟45个字,结果提前20分钟抄完,求这篇文章
的字数.
【解析】设这篇文章的 有x个字,则
解得x=1 800,所以
答:这篇文章的字数为3 000字.【一题多解】设这篇文章有x个字,则 方程变形
为 解得x=3 000.
答:这篇文章的字数为3 000字.5.七年级一班全体学生参加课外活动,原来每组8人;后来根
据需要重新编组,比原来少了3组,每组14人.求这个班的人数.
【解析】设这个班共有学生x人,则
解得x=56.
答:这个班共有56人.【想一想错在哪?】解方程:
提示:去分母时,不能漏乘不含分母的项,分子是多项式的要
加括号.
