2022-2023学年重庆市渝中区、九龙坡区等四区高二(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年重庆市渝中区、九龙坡区等四区高二(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 409.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 12:20:52 | ||
图片预览




文档简介
2022-2023学年重庆市渝中区、九龙坡区等四区高二(下)期末数学试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 命题:,的否定是( )
A. B.
C. D.
2. 已知集合,,则( )
A. B.
C. D.
3. 已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为,则该队员每次罚球的命中率为( )
A. B. C. D.
4. “回文联”是对联中的一种,既可顺读,也可倒读比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天,由此定义“回文数”,为自然数,且的各位数字反向排列所得自然数与相等,这样的称为“回文数”,如:,则所有位数中是“回文数”且各位数字不全相同的共有( )
A. 个 B. 个 C. 个 D. 个
5. 已知,则( )
A. B. C. D.
6. 已知,,,则是成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7. 五声音阶是中国古乐基本音阶,故有成语“五音不全”,中国古乐中的五声音阶依次为:宫、商、角、徵、羽,若把这五个音阶全用上,排成一个五个音阶的音序,且要求宫、羽两音阶不相邻且在角音阶的同侧,则可排成不同的音序种数为( )
A. B. C. D.
8. 已知是自然对数的底数,则下列不等关系中正确的是( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 已知二项式的展开式中各项系数之和是,则下列说法正确的有( )
A. 展开式共有项 B. 二项式系数最大的项是第项
C. 展开式的常数项为 D. 展开式的有理项共有项
10. 假设某市场供应的智能手机中,市场占有率和优质率的信息如下表:
品牌 甲 乙 其他
市场占有率
优质率
在该市场中任意买一部智能手机,用,,分别表示买到的智能手机为甲品牌、乙品牌、其他品牌,表示买到的是优质品,则( )
A. B. C. D.
11. 已知,,且,则下列说法正确的是( )
A. 的最大值是 B. 的最小值是
C. 的最小值是 D. 的最小值是
12. 设为自然对数的底数,函数,则下列结论正确的是( )
A. 当时,无极值点 B. 当时,有两个零点
C. 当时,有个零点 D. 当时,无零点
三、填空题(本大题共4小题,共20.0分)
13. 设离散型随机变量的分布列为:
则离散型随机变量的方差 ______ .
14. 设集合,,若,则实数所有取值组成的集合的子集个数为______ .
15. 某学校要对如图所示的个区域进行绿化种花,现有种不同颜色的花供选择,要求相邻区域不能种同一种颜色的花,则共有______种不同的种花方法.
16. 排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得分,得分的队有发球权,最后先得分的队获得本局比赛胜利,若出现比分:,要继续比赛至某队领先分才能取胜,该局比赛结束,甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为,乙队发球时甲队获胜的概率为,且各次发球的胜负结果相互独立若此时甲、乙两队双方比分为:平,且甲队拥有发球权,则两队共再发次球就结束比赛的概率为______ ;若此时甲、乙两队双方比分为:平,且甲队拥有发球权,则甲队得分且取得该局比赛胜利的概率为______ .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知函数表示的曲线过原点,且此曲线在处的切线斜率均为.
求,,的值;
当时,求的最大值和最小值.
18. 本小题分
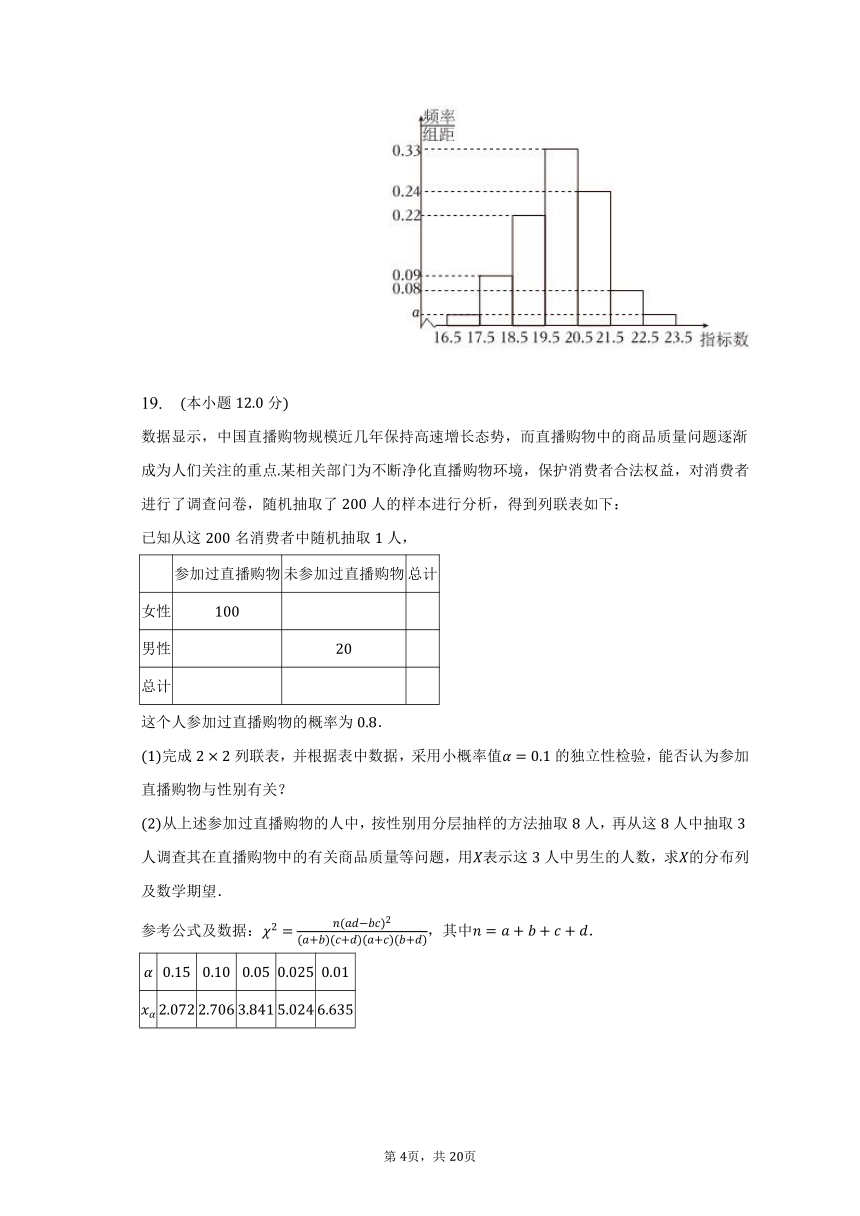
为了提高生产效率,某企业引进一条新的生产线,现要定期对产品进行检测每次抽取件产品作为样本,检测新产品中的某项质量指标数,根据测量结果得到如下频率分布直方图.
若该产品指标数不在区间的产品为次等品,试估计产品为次等品的概率;
技术评估可以认为,这种产品的质量指标数服从正态分布,其中近似为样本的平均数同一组中的数据用该组区间的中点值为代表,计算的值,并计算产品指标数小于的概率.
参考数据:,,.
19. 本小题分
数据显示,中国直播购物规模近几年保持高速增长态势,而直播购物中的商品质量问题逐渐成为人们关注的重点某相关部门为不断净化直播购物环境,保护消费者合法权益,对消费者进行了调查问卷,随机抽取了人的样本进行分析,得到列联表如下:
已知从这名消费者中随机抽取人,
参加过直播购物 未参加过直播购物 总计
女性
男性
总计
这个人参加过直播购物的概率为.
完成列联表,并根据表中数据,采用小概率值的独立性检验,能否认为参加直播购物与性别有关?
从上述参加过直播购物的人中,按性别用分层抽样的方法抽取人,再从这人中抽取人调查其在直播购物中的有关商品质量等问题,用表示这人中男生的人数,求的分布列及数学期望.
参考公式及数据:,其中.
20. 本小题分
教育部决定自年起,在部分高校开展基础学科招生改革试点也称强基计划强基计划主要选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,强基计划的校考由试点高校自主命题,校考过程中通过笔试后才能进入面试环节.
为了更好的服务于高三学生,某研究机构对随机抽取的名高三学生的记忆力和判断力进行统计分析,得到下表数据:
若该组数据中与之间的关系可用线性回归模型进行拟合,求关于的线性回归方程.
根据规定每名考生只能报考强基计划的一所试点高校,某考生准备从甲、乙两所大学选择一所报考,已知甲、乙两所大学的笔试环节都设有三门考试科目,且每门科目是否通过相互独立,若该考生报考甲大学,每门笔试科目通过的概率分别为,,,该考生报考乙大学,每门笔试科目通过的概率均为若以笔试过程中通过科目数的数学期望为依据作出决策,该考生应报考哪所高校.
参考公式:
对于一组数据,,,,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
21. 本小题分
已知函数的导函数为,.
若函数是增函数,求实数的取值范围;
设,当时,若,满足,证明:.
22. 本小题分
已知函数,.
讨论函数的单调区间;
若,证明:;
当时,恒成立,求的取值范围.
答案和解析
1.【答案】
【解析】解:命题:,的否定是,.
故选:.
含有全称量词的命题的否定:将全称改成特称,并对命题否定.
本题考查含有全称量词的命题的否定,属于基础题.
2.【答案】
【解析】解:集合,,
或,
则.
故选:.
求出集合,,再利用交集定义求出.
本题考查集合的运算,考查交集、补集定义、不等式性质等基础知识,考查运算求解能力,是基础题.
3.【答案】
【解析】解:某篮球队员在比赛中每次罚球的命中率相同,
设该队员每次罚球的命中率为,
设“在两次罚球中至多命中一次”为事件,
则“在两次罚球中命中两次”为事件,
,解得:.
故选:.
根据题意,分析可得两次罚球都命中的概率为,由相互独立事件的概率公式可得关于的方程,即可求得结果.
本题考查互斥事件的概率公式,属于基础题.
4.【答案】
【解析】解:根据题意,位“回文数”的十万位数字不能为,有种情况,万位、千位数字都有种情况,
则位“回文数”共有个,
其中,各位数字完全相同的情况有种,
则所有位数中是“回文数”且各位数字不全相同的共有个,
故选:.
根据题意,用间接法分析,先计算全部的五位“回文数”的数目,排除其中各位数字完全相同的情况,即可得答案.
本题考查排列组合的实际应用,注意间接法分析,属于基础题.
5.【答案】
【解析】解:,
令,可得.
再令,可得,
.
故选:.
在所给的式子中,分别令,,即可求得要求式子的值.
本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.
6.【答案】
【解析】解:充分性:,所以,,
即,满足充分性.
必要性:因为,所以,
所以,
即,则,满足必要性.
所以是成立的充要条件.
故选:.
分别判断充分性和必要性即可得到答案.
本题考查充分必要条件,属于基础题.
7.【答案】
【解析】解:若角音阶排在两端,则宫,羽两音阶一定在角音阶的同侧,此时有种,
若确音阶排在正中间,则不可能出现宫、羽两音阶不相邻且在角音阶的同侧的情况,
若角音阶排在第二或第四个位置上,则有种排法,
根据分类加法计数原理可得共有种排法.
故选:.
根据角音阶的位置分类,然后利用插空法可求出结果.
本题考查排列组合的应用,属于中档题.
8.【答案】
【解析】解:对于:令,,则,
由得,由得,由得,
在上单调递增,在上单调递减,
,
,,,
,,,故A、B错误,C正确;
对于:令,则,
由得,由得,由得,
在上单调递增,在上单调递减,
,即,即,故D错误.
故选:.
构造函数,,求导分析单调性,可得,构造函数,则,求出的单调性,即可得出答案.
本题考查利用导数研究函数的单调性,考查转化思想和函数思想,考查逻辑推理能力和运算能力,属于中档题.
9.【答案】
【解析】解:二项式的展开式中各项系数之和是,,故展开式共计有项,故A错误.
根据二项式系数的性质可得,当时,二项式系数最大,故二项式系数最大的项是第项,故B正确.
通项公式为,
令,求得,故展开式的常数项为,故C正确.
令为整数,可得,,,,可得展开式的有理项共有项,故D正确.
故选:.
由题意,利用二项式展开式的通项公式,逐一判断各个选是否正项确,从而得出结论.
本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.
10.【答案】
【解析】解:由表格中的数据可得,,,
,,,
对于选项,,错;
对于选项,,对;
对于选项,,错;
对于选项,,对.
故选:.
利用条件概率公式可判断选项;利用表格中的数据可判断选项;利用全概率公式可判断选项.
本题考查条件概率计算公式,属于基础题.
11.【答案】
【解析】解:因为,,且,
所以,当且仅当时取等号,
解得,所以的最大值是,故A正确;
因为,当且仅当时取等号,
解得,所以的最小值是,故B正确;
由题意得,
所以,
,
当且仅当,即时取等号,故等号不成立,故C错误;
,
当且仅当,即时取等号,故的最小值是,故D错误.
故选:.
由已知结合基本不等式及相关结论分别检验各选项即可判断.
本题主要考查基本不等式的应用,考查运算求解能力,属于中档题.
12.【答案】
【解析】解:,,
当时,,
故,无极值点,故A正确;
当时,,,时,递增,
时,递减,且,
即在上有个零点,故B错误;
当时,,,时,递增,
时,递减,,
上有个零点,故C正确;
当时,,在递减,在递增,
,无零点,故D正确.
故选:.
求出函数的导数,取,得到A正确,通过讨论的范围,求出函数的单调区间,结合函数的单调性判断.
本题考查了函数的单调性,极值,零点问题,考查导数的应用以及分类讨论思想,是中档题.
13.【答案】
【解析】解:由分布列可得,
所以.
故答案为:.
先求期望,再利用方差公式求解方差.
本题考查了离散型随机变量的方差计算,属于基础题.
14.【答案】
【解析】解:因为,,,则.
当时,,合乎题意;当时,,
则或,解得或,
综上所述,实数的取值构成的集合为,
其子集个数为个.
故答案为:.
解出集合,分、两种情况讨论,结合可得出实数的取值集合.
本题考查集合的子集关系,属于基础题.
15.【答案】
【解析】解:根据题意,分步进行分析:
,对于区域,有种颜色可选,即有种着色方法,
,对于区域,与区域相邻,有种颜色可选,即有种着色方法,
,对于区域,与区域、相邻,有种颜色可选,即有种着色方法,
,对于区域,若其颜色与区域的相同,区域有种颜色可选,
若其颜色与区域的不同,区域有种颜色可选,区域有种颜色可选,
则区域、共有种着色方法;
则一共有种着色方法;
故答案为:
根据题意,分步进行分析:依次分析各个区域的着色方法数目,由分步计数原理计算可得答案
本题考查排列、组合的应用,本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色.
16.【答案】
【解析】解:后两队共发次球就结束比赛,则这两个球均由甲队得分,或均由乙队得分,且两者互斥,
记事件“后两队共发次球就结束比赛”,因为各次发球的胜负结果相互独立,
所以,
即后两队共发次球就结束比赛的概率为,
时,甲队得分且取得该局比赛胜利,则甲以:或:取得该局胜利,
记事件“甲以:取得该局胜利”,“甲以:取得该局胜利”,
“时,甲队得分且取得该局比赛胜利”,
因为各次发球的胜负结果相互独立,且,互斥,
所以,
,
,
所以时,甲队得分且取得该局比赛胜利的概率为.
故答案为:.
填空:先确定后两队共发次球就结束比赛,包含这两个球均由甲队得分和这两个球均由乙队得分两个事件,再利用事件的相互独立性求概率;
填空:先确定时,甲队得分且取得该局比赛胜利,包含甲以:取得比赛胜利和甲以:取得胜利两个事件,再利用事件的相互独立性求概率.
本题考查相互独立事件的概率乘法公式,属于基础题.
17.【答案】解:函数,
,
函数表示的曲线过原点,且此曲线在处的切线斜率均为,
,,,
联立解得,,.
由可得,
,
令,解得,
函数在上单调递增,在上单调递减,在上单调递增.
又,,,.
的最大值和最小值分别为,.
【解析】函数,利用导数的运算法则可得,根据函数表示的曲线过原点,且此曲线在处的切线斜率均为,可得,,,联立解得,,.
由可得,令,解得,研究函数的单调性与极值,求出极值与区间端点的函数值,通过比较即可得出结论.
本题考查了利用导数研究函数的单调性与极值及最值、切线的斜率、方程的解法,考查了推理能力与计算能力,属于中档题.
18.【答案】解:由频率分布直方图可得,,
解得,
故次等品的概率为;
这种产品的质量指标数服从正态分布,其中近似为样本的平均数,
,
这种产品的质量指标数服从正态分布,
.
【解析】根据已知条件,结合频率分布直方图的性质,即可求解.
结合平均数公式,即可求解,再结合正态分布的公式,即可求解.
本题主要考查正态分布的性质,以及频率分布直方图的性质,属于基础题.
19.【答案】解:由题意,参加直播购物的总人数为人,其中有名女生,则有男生名,则可得下表:
参加过直播购物 未参加过直播购物 总计
女性
男性
总计
由表格可知:,
由,则认为参加直播购物与性别有关的犯错概率超过,故不能;
由题意,抽取的人中女生的人数为,男生的人数为,
则随机变量可能的取值有,,,,
.
故随机变量的分布列,如下表:
则其数学期望.
【解析】由题意,求出参加直播购物的总人数,完成列联表,利用独立性检验的公式,结合其相关知识,可得答案;
根据分成抽样的相关知识,求得男生女生的人数,根据超几何分布的计算步骤,可得答案.
本题考查了独立性检验和离散型随机变量的分布列与期望,属于中档题.
20.【答案】解:由表格中的数据可得,
所以,,
,
所以,,
因此,关于的线性回归方程为;
解:设该考生报考甲、乙大学笔试过程中通过科目数分别为、,
由题意可知,随机变量的取值有、、、,
则,
,
,
所以,,
由题意可知,,则,
所以,,故建议该考生报考甲大学.
【解析】计算出的值,将表格中的数据代入最小二乘法公式,求出的值,即可得出关于的线性回归方程;
设该考生报考甲、乙大学笔试过程中通过科目数分别为、,根据题意求出、的值,比较大小后可得出结论.
本题考查了线性回归方程和离散型随机变量的期望计算,属于中档题.
21.【答案】解:的定义域为,
,
因为是增函数,
所以任意,恒成立,
所以任意,恒成立,
即任意,恒成立,
令,,
,
令得,
所以在上,单调递增,
在上,单调递减,
所以,
所以,
所以的取值范围为
证明:根据题意可得,,
若,满足,则有两个零点,
所以,
所以,
所以,
要证,
即证,
即证,
即证,
令,
因为,
所以,
所以只需证,
即证,
令,,
,
令,,
,
因为,
所以,
所以在上单调递增,
所以,
所以,
所以在上单调递减,
所以,
所以,得证.
【解析】求导分析的单调性,则任意,恒成立,即任意,恒成立,令,,只需,即可得出答案.
根据题意可得,,若,满足,则有两个零点,则,进而可得,要证,即证,即可得出答案.
本题考查导数的综合应用,解题中需要理清思路,属于中档题.
22.【答案】解:的定义域为,
,
当时,恒成立,
所以在上单调递增,
当时,令得,
所以在上,单调递减,
在上,单调递增,
综上所述,当时,在上单调递增,
当时,在上单调递减,在上单调递增.
当时,,
要证不等式,
即证,
即证,
即证,
即证,
令,,则只需证明,
令,,则只需证,
,
所以在上单调递增,
所以,
,,
所以在上,单调递减,
在上,单调递增,
所以,得证.
若当时,恒成立,
则当时,恒成立,
所以当时,恒成立,
所以当时,恒成立,
设,,则,
,
所以在上单调递增,
所以,,
所以在上,恒成立,
令,,
,
令得,
所以在上,单调递减,
在上,单调递增,
所以,
所以,
所以的取值范围为.
【解析】的定义域为,,分两种情况:当时,当时,分析的符号,的单调性.
当时,要证不等式,即证,令,,则只需证明,即可得出答案.
若当时,恒成立,则当时,恒成立,设,,则,分析的单调性,即可得出在上,恒成立,
令,,只需,即可得出答案.
本题考查导数的综合应用,解题中需要理清思路,属于中档题.
第1页,共1页
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 命题:,的否定是( )
A. B.
C. D.
2. 已知集合,,则( )
A. B.
C. D.
3. 已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为,则该队员每次罚球的命中率为( )
A. B. C. D.
4. “回文联”是对联中的一种,既可顺读,也可倒读比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天,由此定义“回文数”,为自然数,且的各位数字反向排列所得自然数与相等,这样的称为“回文数”,如:,则所有位数中是“回文数”且各位数字不全相同的共有( )
A. 个 B. 个 C. 个 D. 个
5. 已知,则( )
A. B. C. D.
6. 已知,,,则是成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7. 五声音阶是中国古乐基本音阶,故有成语“五音不全”,中国古乐中的五声音阶依次为:宫、商、角、徵、羽,若把这五个音阶全用上,排成一个五个音阶的音序,且要求宫、羽两音阶不相邻且在角音阶的同侧,则可排成不同的音序种数为( )
A. B. C. D.
8. 已知是自然对数的底数,则下列不等关系中正确的是( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 已知二项式的展开式中各项系数之和是,则下列说法正确的有( )
A. 展开式共有项 B. 二项式系数最大的项是第项
C. 展开式的常数项为 D. 展开式的有理项共有项
10. 假设某市场供应的智能手机中,市场占有率和优质率的信息如下表:
品牌 甲 乙 其他
市场占有率
优质率
在该市场中任意买一部智能手机,用,,分别表示买到的智能手机为甲品牌、乙品牌、其他品牌,表示买到的是优质品,则( )
A. B. C. D.
11. 已知,,且,则下列说法正确的是( )
A. 的最大值是 B. 的最小值是
C. 的最小值是 D. 的最小值是
12. 设为自然对数的底数,函数,则下列结论正确的是( )
A. 当时,无极值点 B. 当时,有两个零点
C. 当时,有个零点 D. 当时,无零点
三、填空题(本大题共4小题,共20.0分)
13. 设离散型随机变量的分布列为:
则离散型随机变量的方差 ______ .
14. 设集合,,若,则实数所有取值组成的集合的子集个数为______ .
15. 某学校要对如图所示的个区域进行绿化种花,现有种不同颜色的花供选择,要求相邻区域不能种同一种颜色的花,则共有______种不同的种花方法.
16. 排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得分,得分的队有发球权,最后先得分的队获得本局比赛胜利,若出现比分:,要继续比赛至某队领先分才能取胜,该局比赛结束,甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为,乙队发球时甲队获胜的概率为,且各次发球的胜负结果相互独立若此时甲、乙两队双方比分为:平,且甲队拥有发球权,则两队共再发次球就结束比赛的概率为______ ;若此时甲、乙两队双方比分为:平,且甲队拥有发球权,则甲队得分且取得该局比赛胜利的概率为______ .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知函数表示的曲线过原点,且此曲线在处的切线斜率均为.
求,,的值;
当时,求的最大值和最小值.
18. 本小题分
为了提高生产效率,某企业引进一条新的生产线,现要定期对产品进行检测每次抽取件产品作为样本,检测新产品中的某项质量指标数,根据测量结果得到如下频率分布直方图.
若该产品指标数不在区间的产品为次等品,试估计产品为次等品的概率;
技术评估可以认为,这种产品的质量指标数服从正态分布,其中近似为样本的平均数同一组中的数据用该组区间的中点值为代表,计算的值,并计算产品指标数小于的概率.
参考数据:,,.
19. 本小题分
数据显示,中国直播购物规模近几年保持高速增长态势,而直播购物中的商品质量问题逐渐成为人们关注的重点某相关部门为不断净化直播购物环境,保护消费者合法权益,对消费者进行了调查问卷,随机抽取了人的样本进行分析,得到列联表如下:
已知从这名消费者中随机抽取人,
参加过直播购物 未参加过直播购物 总计
女性
男性
总计
这个人参加过直播购物的概率为.
完成列联表,并根据表中数据,采用小概率值的独立性检验,能否认为参加直播购物与性别有关?
从上述参加过直播购物的人中,按性别用分层抽样的方法抽取人,再从这人中抽取人调查其在直播购物中的有关商品质量等问题,用表示这人中男生的人数,求的分布列及数学期望.
参考公式及数据:,其中.
20. 本小题分
教育部决定自年起,在部分高校开展基础学科招生改革试点也称强基计划强基计划主要选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,强基计划的校考由试点高校自主命题,校考过程中通过笔试后才能进入面试环节.
为了更好的服务于高三学生,某研究机构对随机抽取的名高三学生的记忆力和判断力进行统计分析,得到下表数据:
若该组数据中与之间的关系可用线性回归模型进行拟合,求关于的线性回归方程.
根据规定每名考生只能报考强基计划的一所试点高校,某考生准备从甲、乙两所大学选择一所报考,已知甲、乙两所大学的笔试环节都设有三门考试科目,且每门科目是否通过相互独立,若该考生报考甲大学,每门笔试科目通过的概率分别为,,,该考生报考乙大学,每门笔试科目通过的概率均为若以笔试过程中通过科目数的数学期望为依据作出决策,该考生应报考哪所高校.
参考公式:
对于一组数据,,,,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
21. 本小题分
已知函数的导函数为,.
若函数是增函数,求实数的取值范围;
设,当时,若,满足,证明:.
22. 本小题分
已知函数,.
讨论函数的单调区间;
若,证明:;
当时,恒成立,求的取值范围.
答案和解析
1.【答案】
【解析】解:命题:,的否定是,.
故选:.
含有全称量词的命题的否定:将全称改成特称,并对命题否定.
本题考查含有全称量词的命题的否定,属于基础题.
2.【答案】
【解析】解:集合,,
或,
则.
故选:.
求出集合,,再利用交集定义求出.
本题考查集合的运算,考查交集、补集定义、不等式性质等基础知识,考查运算求解能力,是基础题.
3.【答案】
【解析】解:某篮球队员在比赛中每次罚球的命中率相同,
设该队员每次罚球的命中率为,
设“在两次罚球中至多命中一次”为事件,
则“在两次罚球中命中两次”为事件,
,解得:.
故选:.
根据题意,分析可得两次罚球都命中的概率为,由相互独立事件的概率公式可得关于的方程,即可求得结果.
本题考查互斥事件的概率公式,属于基础题.
4.【答案】
【解析】解:根据题意,位“回文数”的十万位数字不能为,有种情况,万位、千位数字都有种情况,
则位“回文数”共有个,
其中,各位数字完全相同的情况有种,
则所有位数中是“回文数”且各位数字不全相同的共有个,
故选:.
根据题意,用间接法分析,先计算全部的五位“回文数”的数目,排除其中各位数字完全相同的情况,即可得答案.
本题考查排列组合的实际应用,注意间接法分析,属于基础题.
5.【答案】
【解析】解:,
令,可得.
再令,可得,
.
故选:.
在所给的式子中,分别令,,即可求得要求式子的值.
本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.
6.【答案】
【解析】解:充分性:,所以,,
即,满足充分性.
必要性:因为,所以,
所以,
即,则,满足必要性.
所以是成立的充要条件.
故选:.
分别判断充分性和必要性即可得到答案.
本题考查充分必要条件,属于基础题.
7.【答案】
【解析】解:若角音阶排在两端,则宫,羽两音阶一定在角音阶的同侧,此时有种,
若确音阶排在正中间,则不可能出现宫、羽两音阶不相邻且在角音阶的同侧的情况,
若角音阶排在第二或第四个位置上,则有种排法,
根据分类加法计数原理可得共有种排法.
故选:.
根据角音阶的位置分类,然后利用插空法可求出结果.
本题考查排列组合的应用,属于中档题.
8.【答案】
【解析】解:对于:令,,则,
由得,由得,由得,
在上单调递增,在上单调递减,
,
,,,
,,,故A、B错误,C正确;
对于:令,则,
由得,由得,由得,
在上单调递增,在上单调递减,
,即,即,故D错误.
故选:.
构造函数,,求导分析单调性,可得,构造函数,则,求出的单调性,即可得出答案.
本题考查利用导数研究函数的单调性,考查转化思想和函数思想,考查逻辑推理能力和运算能力,属于中档题.
9.【答案】
【解析】解:二项式的展开式中各项系数之和是,,故展开式共计有项,故A错误.
根据二项式系数的性质可得,当时,二项式系数最大,故二项式系数最大的项是第项,故B正确.
通项公式为,
令,求得,故展开式的常数项为,故C正确.
令为整数,可得,,,,可得展开式的有理项共有项,故D正确.
故选:.
由题意,利用二项式展开式的通项公式,逐一判断各个选是否正项确,从而得出结论.
本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.
10.【答案】
【解析】解:由表格中的数据可得,,,
,,,
对于选项,,错;
对于选项,,对;
对于选项,,错;
对于选项,,对.
故选:.
利用条件概率公式可判断选项;利用表格中的数据可判断选项;利用全概率公式可判断选项.
本题考查条件概率计算公式,属于基础题.
11.【答案】
【解析】解:因为,,且,
所以,当且仅当时取等号,
解得,所以的最大值是,故A正确;
因为,当且仅当时取等号,
解得,所以的最小值是,故B正确;
由题意得,
所以,
,
当且仅当,即时取等号,故等号不成立,故C错误;
,
当且仅当,即时取等号,故的最小值是,故D错误.
故选:.
由已知结合基本不等式及相关结论分别检验各选项即可判断.
本题主要考查基本不等式的应用,考查运算求解能力,属于中档题.
12.【答案】
【解析】解:,,
当时,,
故,无极值点,故A正确;
当时,,,时,递增,
时,递减,且,
即在上有个零点,故B错误;
当时,,,时,递增,
时,递减,,
上有个零点,故C正确;
当时,,在递减,在递增,
,无零点,故D正确.
故选:.
求出函数的导数,取,得到A正确,通过讨论的范围,求出函数的单调区间,结合函数的单调性判断.
本题考查了函数的单调性,极值,零点问题,考查导数的应用以及分类讨论思想,是中档题.
13.【答案】
【解析】解:由分布列可得,
所以.
故答案为:.
先求期望,再利用方差公式求解方差.
本题考查了离散型随机变量的方差计算,属于基础题.
14.【答案】
【解析】解:因为,,,则.
当时,,合乎题意;当时,,
则或,解得或,
综上所述,实数的取值构成的集合为,
其子集个数为个.
故答案为:.
解出集合,分、两种情况讨论,结合可得出实数的取值集合.
本题考查集合的子集关系,属于基础题.
15.【答案】
【解析】解:根据题意,分步进行分析:
,对于区域,有种颜色可选,即有种着色方法,
,对于区域,与区域相邻,有种颜色可选,即有种着色方法,
,对于区域,与区域、相邻,有种颜色可选,即有种着色方法,
,对于区域,若其颜色与区域的相同,区域有种颜色可选,
若其颜色与区域的不同,区域有种颜色可选,区域有种颜色可选,
则区域、共有种着色方法;
则一共有种着色方法;
故答案为:
根据题意,分步进行分析:依次分析各个区域的着色方法数目,由分步计数原理计算可得答案
本题考查排列、组合的应用,本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色.
16.【答案】
【解析】解:后两队共发次球就结束比赛,则这两个球均由甲队得分,或均由乙队得分,且两者互斥,
记事件“后两队共发次球就结束比赛”,因为各次发球的胜负结果相互独立,
所以,
即后两队共发次球就结束比赛的概率为,
时,甲队得分且取得该局比赛胜利,则甲以:或:取得该局胜利,
记事件“甲以:取得该局胜利”,“甲以:取得该局胜利”,
“时,甲队得分且取得该局比赛胜利”,
因为各次发球的胜负结果相互独立,且,互斥,
所以,
,
,
所以时,甲队得分且取得该局比赛胜利的概率为.
故答案为:.
填空:先确定后两队共发次球就结束比赛,包含这两个球均由甲队得分和这两个球均由乙队得分两个事件,再利用事件的相互独立性求概率;
填空:先确定时,甲队得分且取得该局比赛胜利,包含甲以:取得比赛胜利和甲以:取得胜利两个事件,再利用事件的相互独立性求概率.
本题考查相互独立事件的概率乘法公式,属于基础题.
17.【答案】解:函数,
,
函数表示的曲线过原点,且此曲线在处的切线斜率均为,
,,,
联立解得,,.
由可得,
,
令,解得,
函数在上单调递增,在上单调递减,在上单调递增.
又,,,.
的最大值和最小值分别为,.
【解析】函数,利用导数的运算法则可得,根据函数表示的曲线过原点,且此曲线在处的切线斜率均为,可得,,,联立解得,,.
由可得,令,解得,研究函数的单调性与极值,求出极值与区间端点的函数值,通过比较即可得出结论.
本题考查了利用导数研究函数的单调性与极值及最值、切线的斜率、方程的解法,考查了推理能力与计算能力,属于中档题.
18.【答案】解:由频率分布直方图可得,,
解得,
故次等品的概率为;
这种产品的质量指标数服从正态分布,其中近似为样本的平均数,
,
这种产品的质量指标数服从正态分布,
.
【解析】根据已知条件,结合频率分布直方图的性质,即可求解.
结合平均数公式,即可求解,再结合正态分布的公式,即可求解.
本题主要考查正态分布的性质,以及频率分布直方图的性质,属于基础题.
19.【答案】解:由题意,参加直播购物的总人数为人,其中有名女生,则有男生名,则可得下表:
参加过直播购物 未参加过直播购物 总计
女性
男性
总计
由表格可知:,
由,则认为参加直播购物与性别有关的犯错概率超过,故不能;
由题意,抽取的人中女生的人数为,男生的人数为,
则随机变量可能的取值有,,,,
.
故随机变量的分布列,如下表:
则其数学期望.
【解析】由题意,求出参加直播购物的总人数,完成列联表,利用独立性检验的公式,结合其相关知识,可得答案;
根据分成抽样的相关知识,求得男生女生的人数,根据超几何分布的计算步骤,可得答案.
本题考查了独立性检验和离散型随机变量的分布列与期望,属于中档题.
20.【答案】解:由表格中的数据可得,
所以,,
,
所以,,
因此,关于的线性回归方程为;
解:设该考生报考甲、乙大学笔试过程中通过科目数分别为、,
由题意可知,随机变量的取值有、、、,
则,
,
,
所以,,
由题意可知,,则,
所以,,故建议该考生报考甲大学.
【解析】计算出的值,将表格中的数据代入最小二乘法公式,求出的值,即可得出关于的线性回归方程;
设该考生报考甲、乙大学笔试过程中通过科目数分别为、,根据题意求出、的值,比较大小后可得出结论.
本题考查了线性回归方程和离散型随机变量的期望计算,属于中档题.
21.【答案】解:的定义域为,
,
因为是增函数,
所以任意,恒成立,
所以任意,恒成立,
即任意,恒成立,
令,,
,
令得,
所以在上,单调递增,
在上,单调递减,
所以,
所以,
所以的取值范围为
证明:根据题意可得,,
若,满足,则有两个零点,
所以,
所以,
所以,
要证,
即证,
即证,
即证,
令,
因为,
所以,
所以只需证,
即证,
令,,
,
令,,
,
因为,
所以,
所以在上单调递增,
所以,
所以,
所以在上单调递减,
所以,
所以,得证.
【解析】求导分析的单调性,则任意,恒成立,即任意,恒成立,令,,只需,即可得出答案.
根据题意可得,,若,满足,则有两个零点,则,进而可得,要证,即证,即可得出答案.
本题考查导数的综合应用,解题中需要理清思路,属于中档题.
22.【答案】解:的定义域为,
,
当时,恒成立,
所以在上单调递增,
当时,令得,
所以在上,单调递减,
在上,单调递增,
综上所述,当时,在上单调递增,
当时,在上单调递减,在上单调递增.
当时,,
要证不等式,
即证,
即证,
即证,
即证,
令,,则只需证明,
令,,则只需证,
,
所以在上单调递增,
所以,
,,
所以在上,单调递减,
在上,单调递增,
所以,得证.
若当时,恒成立,
则当时,恒成立,
所以当时,恒成立,
所以当时,恒成立,
设,,则,
,
所以在上单调递增,
所以,,
所以在上,恒成立,
令,,
,
令得,
所以在上,单调递减,
在上,单调递增,
所以,
所以,
所以的取值范围为.
【解析】的定义域为,,分两种情况:当时,当时,分析的符号,的单调性.
当时,要证不等式,即证,令,,则只需证明,即可得出答案.
若当时,恒成立,则当时,恒成立,设,,则,分析的单调性,即可得出在上,恒成立,
令,,只需,即可得出答案.
本题考查导数的综合应用,解题中需要理清思路,属于中档题.
第1页,共1页
同课章节目录
