2022-2023学年陕西省西安市鄠邑区高二(下)期末数学试卷(文科)(含解析)
文档属性
| 名称 | 2022-2023学年陕西省西安市鄠邑区高二(下)期末数学试卷(文科)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 318.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 12:21:30 | ||
图片预览



文档简介
2022-2023学年陕西省西安市鄠邑区高二(下)期末数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 若,满足,且为纯虚数,则( )
A. B. C. D.
2. 已知点的直角坐标为,则它的柱坐标是( )
A. B. C. D.
3. 若椭圆的参数方程为为参数,则该椭圆的离心率为( )
A. B. C. D.
4. 用反证法证明命题“平面四边形四个内角中至少有一个不大于”时,应假设( )
A. 四个内角都大于 B. 四个内角都不大于
C. 四个内角至多有一个大于 D. 四个内角至多有两个大于
5. 有一散点图如图所示,在个数据中去掉后,下列说法正确的是( )
A. 相关系数变小
B. 残差平方和变小
C. 变量,负相关
D. 解释变量与预报变量的相关性变弱
6. 一组成对数据,,,,样本中心点为,由这组数据拟合的线性回归方程为,用最小二乘法求回归方程是为了使最小.( )
A. 总偏差平方和 B. 残差平方和
C. 回归平方和 D. 竖直距离和
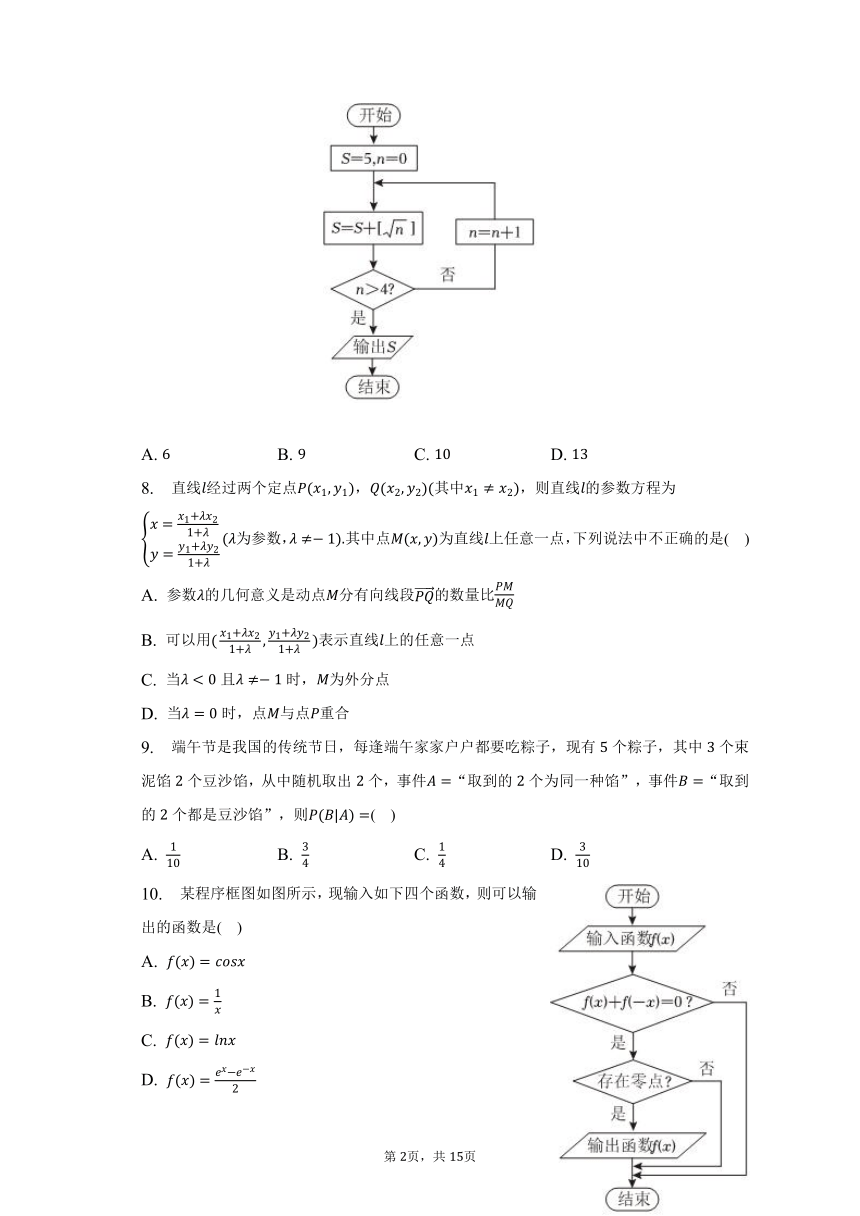
7. 表示不超过的最大整数,执行如图所示的程序框图,则输出的值为( )
A. B. C. D.
8. 直线经过两个定点,其中,则直线的参数方程为为参数,其中点为直线上任意一点,下列说法中不正确的是( )
A. 参数的几何意义是动点分有向线段的数量比
B. 可以用表示直线上的任意一点
C. 当且时,为外分点
D. 当时,点与点重合
9. 端午节是我国的传统节日,每逢端午家家户户都要吃粽子,现有个粽子,其中个束泥馅个豆沙馅,从中随机取出个,事件“取到的个为同一种馅”,事件“取到的个都是豆沙馅”,则( )
A. B. C. D.
10. 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A.
B.
C.
D.
11. 某校课外学习小组研究某作物种子的发芽率和温度单位:的关系,由实验数据得到如图所示的散点图由此散点图判断,最适宜作为发芽率和温度的回归方程类型的是( )
A. B.
C. D.
12. 直线为参数,截抛物线所得的弦长为( )
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
13. 若回归直线方程中的回归系数时,则相关系数 ______ .
14. 已知直线的参数方程为为参数,则直线的倾斜角为______ .
15. 由下列事实:
,
,
,
可得到合理的猜想是______ .
16. 曲线为参数的普通方程为______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知为复数,和均为实数,其中为虚数单位.
求复数和;
若复数在复平面内对应的点位于第三象限,求实数的取值范围.
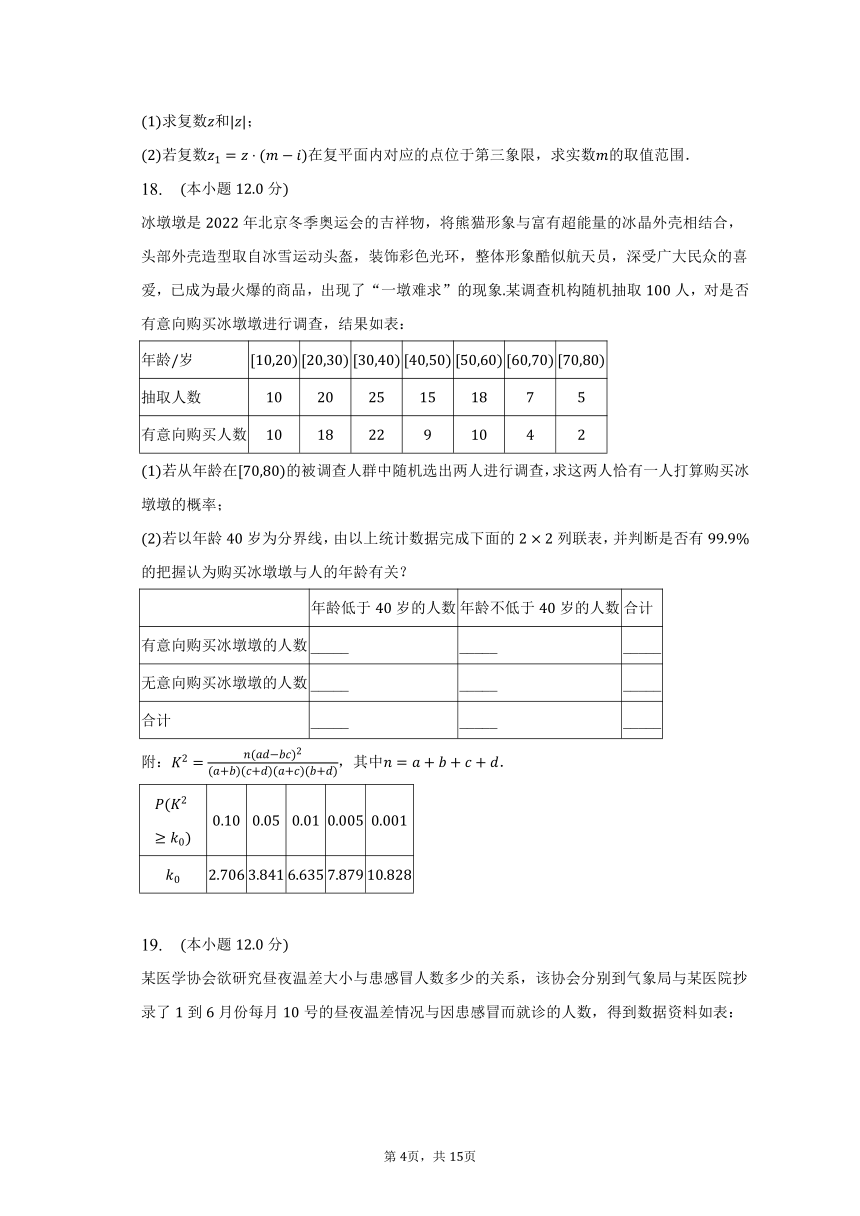
18. 本小题分
冰墩墩是年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员,深受广大民众的喜爱,已成为最火爆的商品,出现了“一墩难求”的现象某调查机构随机抽取人,对是否有意向购买冰墩墩进行调查,结果如表:
年龄岁
抽取人数
有意向购买人数
若从年龄在的被调查人群中随机选出两人进行调查,求这两人恰有一人打算购买冰墩墩的概率;
若以年龄岁为分界线,由以上统计数据完成下面的列联表,并判断是否有的把握认为购买冰墩墩与人的年龄有关?
年龄低于岁的人数 年龄不低于岁的人数 合计
有意向购买冰墩墩的人数 _____ _____ _____
无意向购买冰墩墩的人数 _____ _____ _____
合计 _____ _____ _____
附:,其中.
19. 本小题分
某医学协会欲研究昼夜温差大小与患感冒人数多少的关系,该协会分别到气象局与某医院抄录了到月份每月号的昼夜温差情况与因患感冒而就诊的人数,得到数据资料如表:
月份
昼夜温差
就诊人数个
该协会的研究方案是:先从这六组数据中选取组,用剩下的组数据求线性回归方程,再用被选取的组数据进行检验.
求选取的组数据恰好是相邻的两个月的概率;
已知选取的是月和月的两组数据.
请根据月到月份的数据,求就诊人数关于昼夜温差的线性回归方程若不是整数用分数表示;
若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过人,则认为得到的线性回归方程是理想的,试问该协会所得线性回归方程是否理想?
附:
,
20. 本小题分
在直角坐标系中,曲线的参数方程为,为参数,.
在平面直角坐标系中,画出曲线的图象;
过定点,斜率的直线与曲线只有一个公共点,求的取值范围.
21. 本小题分
用分析法证明:当且仅当时等号成立.
设为曼哈顿扩张距离,其中为正整数如若对一切实数恒成立设,,且,求证:.
22. 本小题分
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为,圆与极轴交于点异于坐标原点,点是圆上的任意一点.
写出点的极坐标和圆的参数方程;
求的最大值.
答案和解析
1.【答案】
【解析】解:,
,
若为纯虚数,
则,解得:.
故选:.
根据复数的运算表示出,根据纯虚数的定义求出的值即可.
本题考查了复数的运算,考查复数的有关定义,是基础题.
2.【答案】
【解析】解:设的柱坐标为,
则,
,解得.
又,
.
故选:.
根据柱坐标与直角坐标的对应关系列方程求出.
本题考查了柱坐标与直角坐标的对应关系,属于基础题.
3.【答案】
【解析】解:根据题意,椭圆的参数方程为为参数,消去参数可得其普通方程为,
则,,则,
故,,
则该椭圆的离心率.
故选:.
由椭圆的参数方程,消去参数可得椭圆的普通方程,从而求出,,利用离心率公式即可求得结果.
本题考查参数方程化为普通方程的方法,涉及椭圆离心率的计算,属于基础题.
4.【答案】
【解析】
【分析】
本题主要考查求一个命题的否定,用反证法证明数学命题,属于基础题.
把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,由此得到答案.
【解答】
证明:用反证法证明命题:“平面四边形四个内角中至少有一个不大于”时,应假设命题的否定成立,
而命题:“平面四边形四个内角中至少有一个不大于”的否定是:假设四个内角都大于,
故选:.
5.【答案】
【解析】解:对于,去掉后,相关性变强,相关系数变大,故A错误;
对于,残差平方和变小,故B正确;
对于,散点的分布是从左下到右上,故变量,正相关,故C错误;
对于,解释变量与预报变量的相关性变强,故D错误.
故选:.
根据散点图的分布以及相关性的相关定义,结合选项即可逐一判断.
本题考查散点图的分布以及相关性的相关定义,属于基础题.
6.【答案】
【解析】解:一组成对数据,,,,,
由这组数据拟合的线性回归方程为,用最小二乘法求回归方程是为了使残差平方和最小.
故选:.
直接由最小二乘法求线性回归方程的意义得结论.
本题考查线性回归方程,考查最小二乘法求线性回归方程的意义,是基础题.
7.【答案】
【解析】解:,,
,,继续执行;
,,
,继续执行;
,,
,继续执行;
,,
,继续执行;
,,
,输出.
故选:.
根据程序框图,按步骤执行命令,即可得出答案.
本题考查程序框图,属于基础题.
8.【答案】
【解析】解:根据题意,依次分析选项:
对于,,其中,则,
,则为参数,,则,
故参数的几何意义是动点分有向线段的数量比,A正确;
对于,结合的结论中数的几何意义,由于,则用不能表示点,B错误;
对于,当且时,不在线段上,即为外分点,C正确;
对于,当时,的坐标为,与点重合,D正确.
故选:.
根据题意,求出和的坐标,由此依次分析选项是否正确,综合可得答案.
本题考查曲线与方程,涉及向量的数乘运算,属于中档题.
9.【答案】
【解析】解:由已知:有个粽子,其中个束泥馅个豆沙馅,随机取出个,
事件“取到的个为同一种馅”,事件“取到的个都是豆沙馅”,
则,,
.
故选:.
分别算出取出的两个粽子是同一种馅,以及两个都是豆沙馅的基本事件个数,然后套用条件概率公式计算即可.
本题考查条件概率的计算公式,以及古典概型的概率计算方法,属于基础题.
10.【答案】
【解析】解::、:,不是奇函数,故不满足条件,
又:的函数图象与轴没有交点,故不满足条件存在零点,
而:既是奇函数,而且函数图象与也有交点,
故D:符合输出的条件.
故选:.
分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件,即函数为奇函数存在零点,即函数图象与轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
本题主要考查程序框图的应用,属于基础题.
11.【答案】
【解析】解:由散点图可见,数据分布成递增趋势,但是呈现上凸效果,即增加缓慢.
中,是直线型,均匀增长,不符合要求;
中,是二次函数型,图象呈现下凸,增长也较快,不符合要求;
中,是指数型,爆炸式增长,增长快,不符合要求;
中,是对数型,增长缓慢,符合要求.
故对数型最适宜该回归模型.
故选:.
根据散点的分布和选项函数模型的特征可得出合适的回归方程类型.
本题考查了利用散点图选择回归模型的问题,属于基础题.
12.【答案】
【解析】解:由为参数,得
直线方程为:,
假设两个交点,,
由,得
所以,,
所以:.
故选:.
先将直线的参数方程化为一般方程,将直线与抛物线方程联立,利用弦长公式求出弦长.
本题考查直线与圆锥曲线相交得到的弦长问题,一般将它们的方程联立,利用弦长公式来解决.
13.【答案】
【解析】解:由于在回归系数的计算公式中,
与相关指数的计算公式中,
它们的分子相同,
故答案为:.
本题考查的知识是线性回归方程的回归系数与相关指数的关系,我们由相关指数的计算公式,与回归系数的计算公式,易得,当时,公式的分子为零,此时相关系数的分子也为,即可得到结果.
相关指数与回归系数存在联系,求解它们的公式分子部分是相同的,如果,则也成立,反之当时,也成立.
14.【答案】
【解析】解:直线的参数方程为为参数,
转换为标准式为,
所以直线的斜率为,
故直线的倾斜角为.
故答案为:.
首先求出直线的参数方程的标准式,进一步利用直线的倾斜角和斜率之间的关系式的应用求出结果.
本题考查的知识要点:直线的参数方程的标准式之间的转化,直线的倾斜角和斜率之间的关系的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.
15.【答案】
【解析】解:由题意,当时,有;
当时,有;
当时,有;
当时,有;
所以得到猜想:当时,有;
故答案为:.
根据所给信息,可知各个等式的左边两因式中,一项为,另一项每一项的次数均为,而且按照字母的降幂排列,故可得答案.
本题的考点是归纳推理,主要考查信息的处理,关键是根据所给信息,可知两因式中,一项为,另一项每一项的次数均为,而且按照字母的降幂排列.
16.【答案】除点
【解析】解:曲线为参数,可知,
消去参数可得:,化简可得除点.
故答案为:除点.
消去参数,即可得到普通方程.
本题考查参数方程与普通方程的互化,是基础题.
17.【答案】解:由和均为实数,
可设,
,
由复数相等可得,解得:,
.
,
在复平面内对应的点位于第三象限,
,解得:,
即的取值范围是.
【解析】分别表示出和,根据对应关系求出参数的值,求出复数和即可;
表示出,根据其在复平面内对应的点位于第三象限,求出的范围即可.
本题考查了复数的有关定义,考查转化思想,是基础题.
18.【答案】解:因为年龄在之间抽取的人数为人,记为,,,,其中,表示有意向购买冰墩墩的人,
从人中抽取人的基本事件有,,,,,,,,,,共个,
其中恰有一人打算购买冰墩墩的基本事件有,,,,,,共个,
则所求概率;
由调查表可得:
年龄低于岁的人数 年龄不低于岁的人数 总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计
,
所以有的把握认为购买冰墩墩与人的年龄有关.
【解析】利用古典概型的概率公式求解;
根据题目所给的数据填写列联表,计算,对照题目中的表格,得出统计结论.
本题主要考查了古典概型的概率公式,考查了独立性检验的应用,属于基础题.
19.【答案】解:从组数据中选出组数据,共有,,,,,,,,,,,,,,种选法.
设事件“抽到相邻两个月的数据”,共包含,,,,个基本事件,
则选取的组数据恰好是相邻的两个月的概率;
由数据求得,,
,.
关于的线性回归方程为;
当时,预估数据,
当时,预估数据.
该协会所得线性回归方程是理想的.
【解析】用枚举法列出所有基本事件总数,得到是相邻两个月的数据的事件数,再由古典概型概率公式求解;
由最小二乘法求得与的值,可得线性回归方程;
利用中求得线性回归方程,取与验证即可得结论.
本题考查古典概型概率的求法,考查线性回归方程及其应用,考查运算求解能力,是中档题.
20.【答案】解:曲线的参数方程为,为参数,.
曲线的普通方程为,
图象为:
过定点,斜率的直线与曲线只有一个公共点,
当直线过点是恰有两个公共点,此时,
当直线与圆相切时,
恰有一个公共点,此时,
所以或.
的取值范围:或.
【解析】化简曲线的参数方程为普通方程,然后画出曲线的图象.
结合图形,转化求解直线的斜率即可.
本题考查参数方程与普通方程的互化,是中档题.
21.【答案】证明:要证明成立,
只需证明成立,
也就是证明,即证,
该式显然成立,
当且仅当时等号成立.
由题意可得,
则对一切实数恒成立,即对一切实数恒成立,
,,即.
由知,,
,
又,,.
【解析】直接利用分析法证明;
由已知利用绝对值的不等式求得的最大值,可得,结合中的距离证明.
本题考查不等式的证明,考查逻辑思维能力与推理论证能力,是中档题.
22.【答案】解:圆的极坐标方程为,圆与极轴交于点异于坐标原点,
令得,
,
由,
可得,
根据,
转化为直角坐标方程为,
配方可得,
所以圆的参数方程为为参数.
点是圆上的任意一点,
设,
,,
其中,,
.
的最大值为.
【解析】令得,求解的坐标,求出圆直角坐标方程为,然后求解圆的参数方程.
设,通过向量的数量积,结合三角函数的最值求解即可.
本题考查极坐标与直角坐标方程的互化,参数方程的应用,是中档题.
第1页,共1页
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 若,满足,且为纯虚数,则( )
A. B. C. D.
2. 已知点的直角坐标为,则它的柱坐标是( )
A. B. C. D.
3. 若椭圆的参数方程为为参数,则该椭圆的离心率为( )
A. B. C. D.
4. 用反证法证明命题“平面四边形四个内角中至少有一个不大于”时,应假设( )
A. 四个内角都大于 B. 四个内角都不大于
C. 四个内角至多有一个大于 D. 四个内角至多有两个大于
5. 有一散点图如图所示,在个数据中去掉后,下列说法正确的是( )
A. 相关系数变小
B. 残差平方和变小
C. 变量,负相关
D. 解释变量与预报变量的相关性变弱
6. 一组成对数据,,,,样本中心点为,由这组数据拟合的线性回归方程为,用最小二乘法求回归方程是为了使最小.( )
A. 总偏差平方和 B. 残差平方和
C. 回归平方和 D. 竖直距离和
7. 表示不超过的最大整数,执行如图所示的程序框图,则输出的值为( )
A. B. C. D.
8. 直线经过两个定点,其中,则直线的参数方程为为参数,其中点为直线上任意一点,下列说法中不正确的是( )
A. 参数的几何意义是动点分有向线段的数量比
B. 可以用表示直线上的任意一点
C. 当且时,为外分点
D. 当时,点与点重合
9. 端午节是我国的传统节日,每逢端午家家户户都要吃粽子,现有个粽子,其中个束泥馅个豆沙馅,从中随机取出个,事件“取到的个为同一种馅”,事件“取到的个都是豆沙馅”,则( )
A. B. C. D.
10. 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A.
B.
C.
D.
11. 某校课外学习小组研究某作物种子的发芽率和温度单位:的关系,由实验数据得到如图所示的散点图由此散点图判断,最适宜作为发芽率和温度的回归方程类型的是( )
A. B.
C. D.
12. 直线为参数,截抛物线所得的弦长为( )
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
13. 若回归直线方程中的回归系数时,则相关系数 ______ .
14. 已知直线的参数方程为为参数,则直线的倾斜角为______ .
15. 由下列事实:
,
,
,
可得到合理的猜想是______ .
16. 曲线为参数的普通方程为______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知为复数,和均为实数,其中为虚数单位.
求复数和;
若复数在复平面内对应的点位于第三象限,求实数的取值范围.
18. 本小题分
冰墩墩是年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员,深受广大民众的喜爱,已成为最火爆的商品,出现了“一墩难求”的现象某调查机构随机抽取人,对是否有意向购买冰墩墩进行调查,结果如表:
年龄岁
抽取人数
有意向购买人数
若从年龄在的被调查人群中随机选出两人进行调查,求这两人恰有一人打算购买冰墩墩的概率;
若以年龄岁为分界线,由以上统计数据完成下面的列联表,并判断是否有的把握认为购买冰墩墩与人的年龄有关?
年龄低于岁的人数 年龄不低于岁的人数 合计
有意向购买冰墩墩的人数 _____ _____ _____
无意向购买冰墩墩的人数 _____ _____ _____
合计 _____ _____ _____
附:,其中.
19. 本小题分
某医学协会欲研究昼夜温差大小与患感冒人数多少的关系,该协会分别到气象局与某医院抄录了到月份每月号的昼夜温差情况与因患感冒而就诊的人数,得到数据资料如表:
月份
昼夜温差
就诊人数个
该协会的研究方案是:先从这六组数据中选取组,用剩下的组数据求线性回归方程,再用被选取的组数据进行检验.
求选取的组数据恰好是相邻的两个月的概率;
已知选取的是月和月的两组数据.
请根据月到月份的数据,求就诊人数关于昼夜温差的线性回归方程若不是整数用分数表示;
若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过人,则认为得到的线性回归方程是理想的,试问该协会所得线性回归方程是否理想?
附:
,
20. 本小题分
在直角坐标系中,曲线的参数方程为,为参数,.
在平面直角坐标系中,画出曲线的图象;
过定点,斜率的直线与曲线只有一个公共点,求的取值范围.
21. 本小题分
用分析法证明:当且仅当时等号成立.
设为曼哈顿扩张距离,其中为正整数如若对一切实数恒成立设,,且,求证:.
22. 本小题分
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为,圆与极轴交于点异于坐标原点,点是圆上的任意一点.
写出点的极坐标和圆的参数方程;
求的最大值.
答案和解析
1.【答案】
【解析】解:,
,
若为纯虚数,
则,解得:.
故选:.
根据复数的运算表示出,根据纯虚数的定义求出的值即可.
本题考查了复数的运算,考查复数的有关定义,是基础题.
2.【答案】
【解析】解:设的柱坐标为,
则,
,解得.
又,
.
故选:.
根据柱坐标与直角坐标的对应关系列方程求出.
本题考查了柱坐标与直角坐标的对应关系,属于基础题.
3.【答案】
【解析】解:根据题意,椭圆的参数方程为为参数,消去参数可得其普通方程为,
则,,则,
故,,
则该椭圆的离心率.
故选:.
由椭圆的参数方程,消去参数可得椭圆的普通方程,从而求出,,利用离心率公式即可求得结果.
本题考查参数方程化为普通方程的方法,涉及椭圆离心率的计算,属于基础题.
4.【答案】
【解析】
【分析】
本题主要考查求一个命题的否定,用反证法证明数学命题,属于基础题.
把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,由此得到答案.
【解答】
证明:用反证法证明命题:“平面四边形四个内角中至少有一个不大于”时,应假设命题的否定成立,
而命题:“平面四边形四个内角中至少有一个不大于”的否定是:假设四个内角都大于,
故选:.
5.【答案】
【解析】解:对于,去掉后,相关性变强,相关系数变大,故A错误;
对于,残差平方和变小,故B正确;
对于,散点的分布是从左下到右上,故变量,正相关,故C错误;
对于,解释变量与预报变量的相关性变强,故D错误.
故选:.
根据散点图的分布以及相关性的相关定义,结合选项即可逐一判断.
本题考查散点图的分布以及相关性的相关定义,属于基础题.
6.【答案】
【解析】解:一组成对数据,,,,,
由这组数据拟合的线性回归方程为,用最小二乘法求回归方程是为了使残差平方和最小.
故选:.
直接由最小二乘法求线性回归方程的意义得结论.
本题考查线性回归方程,考查最小二乘法求线性回归方程的意义,是基础题.
7.【答案】
【解析】解:,,
,,继续执行;
,,
,继续执行;
,,
,继续执行;
,,
,继续执行;
,,
,输出.
故选:.
根据程序框图,按步骤执行命令,即可得出答案.
本题考查程序框图,属于基础题.
8.【答案】
【解析】解:根据题意,依次分析选项:
对于,,其中,则,
,则为参数,,则,
故参数的几何意义是动点分有向线段的数量比,A正确;
对于,结合的结论中数的几何意义,由于,则用不能表示点,B错误;
对于,当且时,不在线段上,即为外分点,C正确;
对于,当时,的坐标为,与点重合,D正确.
故选:.
根据题意,求出和的坐标,由此依次分析选项是否正确,综合可得答案.
本题考查曲线与方程,涉及向量的数乘运算,属于中档题.
9.【答案】
【解析】解:由已知:有个粽子,其中个束泥馅个豆沙馅,随机取出个,
事件“取到的个为同一种馅”,事件“取到的个都是豆沙馅”,
则,,
.
故选:.
分别算出取出的两个粽子是同一种馅,以及两个都是豆沙馅的基本事件个数,然后套用条件概率公式计算即可.
本题考查条件概率的计算公式,以及古典概型的概率计算方法,属于基础题.
10.【答案】
【解析】解::、:,不是奇函数,故不满足条件,
又:的函数图象与轴没有交点,故不满足条件存在零点,
而:既是奇函数,而且函数图象与也有交点,
故D:符合输出的条件.
故选:.
分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件,即函数为奇函数存在零点,即函数图象与轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
本题主要考查程序框图的应用,属于基础题.
11.【答案】
【解析】解:由散点图可见,数据分布成递增趋势,但是呈现上凸效果,即增加缓慢.
中,是直线型,均匀增长,不符合要求;
中,是二次函数型,图象呈现下凸,增长也较快,不符合要求;
中,是指数型,爆炸式增长,增长快,不符合要求;
中,是对数型,增长缓慢,符合要求.
故对数型最适宜该回归模型.
故选:.
根据散点的分布和选项函数模型的特征可得出合适的回归方程类型.
本题考查了利用散点图选择回归模型的问题,属于基础题.
12.【答案】
【解析】解:由为参数,得
直线方程为:,
假设两个交点,,
由,得
所以,,
所以:.
故选:.
先将直线的参数方程化为一般方程,将直线与抛物线方程联立,利用弦长公式求出弦长.
本题考查直线与圆锥曲线相交得到的弦长问题,一般将它们的方程联立,利用弦长公式来解决.
13.【答案】
【解析】解:由于在回归系数的计算公式中,
与相关指数的计算公式中,
它们的分子相同,
故答案为:.
本题考查的知识是线性回归方程的回归系数与相关指数的关系,我们由相关指数的计算公式,与回归系数的计算公式,易得,当时,公式的分子为零,此时相关系数的分子也为,即可得到结果.
相关指数与回归系数存在联系,求解它们的公式分子部分是相同的,如果,则也成立,反之当时,也成立.
14.【答案】
【解析】解:直线的参数方程为为参数,
转换为标准式为,
所以直线的斜率为,
故直线的倾斜角为.
故答案为:.
首先求出直线的参数方程的标准式,进一步利用直线的倾斜角和斜率之间的关系式的应用求出结果.
本题考查的知识要点:直线的参数方程的标准式之间的转化,直线的倾斜角和斜率之间的关系的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.
15.【答案】
【解析】解:由题意,当时,有;
当时,有;
当时,有;
当时,有;
所以得到猜想:当时,有;
故答案为:.
根据所给信息,可知各个等式的左边两因式中,一项为,另一项每一项的次数均为,而且按照字母的降幂排列,故可得答案.
本题的考点是归纳推理,主要考查信息的处理,关键是根据所给信息,可知两因式中,一项为,另一项每一项的次数均为,而且按照字母的降幂排列.
16.【答案】除点
【解析】解:曲线为参数,可知,
消去参数可得:,化简可得除点.
故答案为:除点.
消去参数,即可得到普通方程.
本题考查参数方程与普通方程的互化,是基础题.
17.【答案】解:由和均为实数,
可设,
,
由复数相等可得,解得:,
.
,
在复平面内对应的点位于第三象限,
,解得:,
即的取值范围是.
【解析】分别表示出和,根据对应关系求出参数的值,求出复数和即可;
表示出,根据其在复平面内对应的点位于第三象限,求出的范围即可.
本题考查了复数的有关定义,考查转化思想,是基础题.
18.【答案】解:因为年龄在之间抽取的人数为人,记为,,,,其中,表示有意向购买冰墩墩的人,
从人中抽取人的基本事件有,,,,,,,,,,共个,
其中恰有一人打算购买冰墩墩的基本事件有,,,,,,共个,
则所求概率;
由调查表可得:
年龄低于岁的人数 年龄不低于岁的人数 总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计
,
所以有的把握认为购买冰墩墩与人的年龄有关.
【解析】利用古典概型的概率公式求解;
根据题目所给的数据填写列联表,计算,对照题目中的表格,得出统计结论.
本题主要考查了古典概型的概率公式,考查了独立性检验的应用,属于基础题.
19.【答案】解:从组数据中选出组数据,共有,,,,,,,,,,,,,,种选法.
设事件“抽到相邻两个月的数据”,共包含,,,,个基本事件,
则选取的组数据恰好是相邻的两个月的概率;
由数据求得,,
,.
关于的线性回归方程为;
当时,预估数据,
当时,预估数据.
该协会所得线性回归方程是理想的.
【解析】用枚举法列出所有基本事件总数,得到是相邻两个月的数据的事件数,再由古典概型概率公式求解;
由最小二乘法求得与的值,可得线性回归方程;
利用中求得线性回归方程,取与验证即可得结论.
本题考查古典概型概率的求法,考查线性回归方程及其应用,考查运算求解能力,是中档题.
20.【答案】解:曲线的参数方程为,为参数,.
曲线的普通方程为,
图象为:
过定点,斜率的直线与曲线只有一个公共点,
当直线过点是恰有两个公共点,此时,
当直线与圆相切时,
恰有一个公共点,此时,
所以或.
的取值范围:或.
【解析】化简曲线的参数方程为普通方程,然后画出曲线的图象.
结合图形,转化求解直线的斜率即可.
本题考查参数方程与普通方程的互化,是中档题.
21.【答案】证明:要证明成立,
只需证明成立,
也就是证明,即证,
该式显然成立,
当且仅当时等号成立.
由题意可得,
则对一切实数恒成立,即对一切实数恒成立,
,,即.
由知,,
,
又,,.
【解析】直接利用分析法证明;
由已知利用绝对值的不等式求得的最大值,可得,结合中的距离证明.
本题考查不等式的证明,考查逻辑思维能力与推理论证能力,是中档题.
22.【答案】解:圆的极坐标方程为,圆与极轴交于点异于坐标原点,
令得,
,
由,
可得,
根据,
转化为直角坐标方程为,
配方可得,
所以圆的参数方程为为参数.
点是圆上的任意一点,
设,
,,
其中,,
.
的最大值为.
【解析】令得,求解的坐标,求出圆直角坐标方程为,然后求解圆的参数方程.
设,通过向量的数量积,结合三角函数的最值求解即可.
本题考查极坐标与直角坐标方程的互化,参数方程的应用,是中档题.
第1页,共1页
同课章节目录
