幂的乘方[上学期]
图片预览







文档简介
课件26张PPT。要是我们只限于梦想,
那么,谁来使生活成为美丽的呢?
因此,我们应该抓住今天,
做一个认真做学问的人。
——高尔基 课前复习:同底数幂的乘法:
同底数幂相乘,底数不变,指数相加。am · an = am+n (m、n为正整数)
a2·a3= a5(a4)3104×105=109填一填想一想15.2.2幂的乘方 (1)(32)3=( )×( )×( )=3( )
(2)(a2)3=( )×( )×( )=a( )
(3)(am)3=( )×( )×( )=a( ) (m为正整数)
根据乘方的意义与同底数幂的乘法填空,32323266a2a2a2amamam3m对于任意底数a与任意正整数m、n看看计算的结果有什么规律?
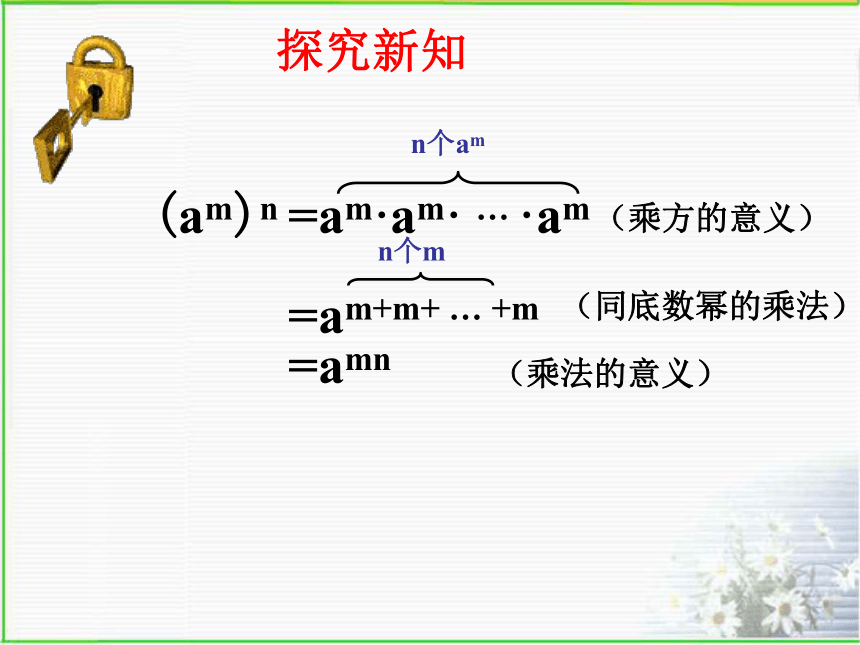
探究新知(am)n (乘方的意义)(同底数幂的乘法) =amn (乘法的意义) 幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则你能用文字语言叙述这个结论吗?底数不变指数相乘
(-5)1+7=(-5)8103+4 =107=58幂的乘方公式
幂的乘方法则
幂的乘方,底数不变,指数相乘。请设计一个幂的乘方运算,让同桌解答。现在你会求(a4)3了吗?(a4)m呢?不变不变指数
相加指数
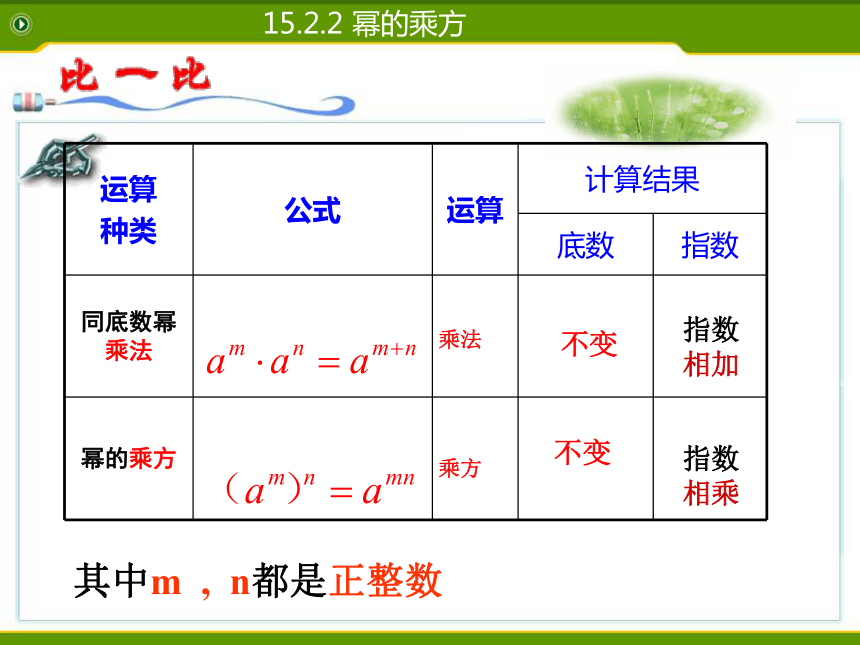
相乘15.2.2 幂的乘方其中m , n都是正整数
乘法乘方解:例 1 计算:
(1)(103)5 (2)(a4)4 (3)(am)2 (4)-(X4)3
(1) (103)5=103×5=1015 (2) (a4)4=a4×4=a16(3) (am)2 =am×2=a2m
(4) -(X4)3=-X4×3=-X12(5)[(a+b)2]5
(5)[(a+b)2]5 =(a+b) 2×5=(a+b)10(6) [ (a3)2 ]4
=a24(6)[ (a3)2 ]4=(a6)4多重乘方(-X4)3
(-X4)3 =-X4×3=-X12
333小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .×(4) (a3 )4+ a12 = 2a24(3)原式= a12 + a12=2a12
××√ 如果甲球的半径是乙球的n倍,
那么甲球的体积是乙球的n3倍。
地球、木星、太阳可以近似地看作球体 .
太阳的半径约是地球的102倍,
那么它的体积约是地球的多少倍?
(102)3=106你真的会了吗?解:原式=例2(1) (b2)3 . b5b6.b5=b11( )( )幂的乘方法则同底数幂的乘法法则你真的会了吗?解:原式=例2(2) a2 a4+( a3)2.a6+a6=2a6⑴ a8 + (a2)4 ⑵ a3 . (a5)2
(3) (a3)2 . a 2a7
(4) (x2 . x3)5
口答题2、a6= a( ) ( )3、x3n=x( )( )=填空x( )( )1、(bm)4= b( )4、ya+b = ya yb4m3nn3.能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!幂的乘方法则的逆用:挑战新高比较 355,444,533 的大小.(不用计算器计算)解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 533
本节课的收获??1、同底数幂的乘法和幂的乘方的区别与联系。
底数不变指数相乘指数相加同底数幂乘法幂的乘方其中m , n都是正整数本节课的收获??1、同底数幂的乘法和幂的乘方的区别与联系。
2、公式中的底数a可以是具体的数,也可以是代数式。
3、多重乘方可以重复运用法则。
amn =(am)n = (an)m
4、幂的乘方逆用再见!!!谢谢各位专家评委1.计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xm)2· (x3)2m ⑷ (a2)3+a3 · a3要认真呀!课堂作业课堂小结1、幂的乘方的法则
15.2.2 幂的乘方(m、n都是正整数)幂的乘方,底数不变,指数相乘。语言叙述 。 符号叙述 。 2、幂的乘方的法则可以逆用。即:3、多重乘方也具有这一性质。如:(其中 m、n、p都是正整数)
那么,谁来使生活成为美丽的呢?
因此,我们应该抓住今天,
做一个认真做学问的人。
——高尔基 课前复习:同底数幂的乘法:
同底数幂相乘,底数不变,指数相加。am · an = am+n (m、n为正整数)
a2·a3= a5(a4)3104×105=109填一填想一想15.2.2幂的乘方 (1)(32)3=( )×( )×( )=3( )
(2)(a2)3=( )×( )×( )=a( )
(3)(am)3=( )×( )×( )=a( ) (m为正整数)
根据乘方的意义与同底数幂的乘法填空,32323266a2a2a2amamam3m对于任意底数a与任意正整数m、n看看计算的结果有什么规律?
探究新知(am)n (乘方的意义)(同底数幂的乘法) =amn (乘法的意义) 幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则你能用文字语言叙述这个结论吗?底数不变指数相乘
(-5)1+7=(-5)8103+4 =107=58幂的乘方公式
幂的乘方法则
幂的乘方,底数不变,指数相乘。请设计一个幂的乘方运算,让同桌解答。现在你会求(a4)3了吗?(a4)m呢?不变不变指数
相加指数
相乘15.2.2 幂的乘方其中m , n都是正整数
乘法乘方解:例 1 计算:
(1)(103)5 (2)(a4)4 (3)(am)2 (4)-(X4)3
(1) (103)5=103×5=1015 (2) (a4)4=a4×4=a16(3) (am)2 =am×2=a2m
(4) -(X4)3=-X4×3=-X12(5)[(a+b)2]5
(5)[(a+b)2]5 =(a+b) 2×5=(a+b)10(6) [ (a3)2 ]4
=a24(6)[ (a3)2 ]4=(a6)4多重乘方(-X4)3
(-X4)3 =-X4×3=-X12
333小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .×(4) (a3 )4+ a12 = 2a24(3)原式= a12 + a12=2a12
××√ 如果甲球的半径是乙球的n倍,
那么甲球的体积是乙球的n3倍。
地球、木星、太阳可以近似地看作球体 .
太阳的半径约是地球的102倍,
那么它的体积约是地球的多少倍?
(102)3=106你真的会了吗?解:原式=例2(1) (b2)3 . b5b6.b5=b11( )( )幂的乘方法则同底数幂的乘法法则你真的会了吗?解:原式=例2(2) a2 a4+( a3)2.a6+a6=2a6⑴ a8 + (a2)4 ⑵ a3 . (a5)2
(3) (a3)2 . a 2a7
(4) (x2 . x3)5
口答题2、a6= a( ) ( )3、x3n=x( )( )=填空x( )( )1、(bm)4= b( )4、ya+b = ya yb4m3nn3.能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!幂的乘方法则的逆用:挑战新高比较 355,444,533 的大小.(不用计算器计算)解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 533
本节课的收获??1、同底数幂的乘法和幂的乘方的区别与联系。
底数不变指数相乘指数相加同底数幂乘法幂的乘方其中m , n都是正整数本节课的收获??1、同底数幂的乘法和幂的乘方的区别与联系。
2、公式中的底数a可以是具体的数,也可以是代数式。
3、多重乘方可以重复运用法则。
amn =(am)n = (an)m
4、幂的乘方逆用再见!!!谢谢各位专家评委1.计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xm)2· (x3)2m ⑷ (a2)3+a3 · a3要认真呀!课堂作业课堂小结1、幂的乘方的法则
15.2.2 幂的乘方(m、n都是正整数)幂的乘方,底数不变,指数相乘。语言叙述 。 符号叙述 。 2、幂的乘方的法则可以逆用。即:3、多重乘方也具有这一性质。如:(其中 m、n、p都是正整数)
