二次函数函数的应用[下学期]

课件13张PPT。6.4二次函数的应用楚州实验中学初三数学备课组1、写出正方体的表面积y与棱长x之间的函数关系式。
2、一个圆柱的高等于它的底面半径r，写出圆柱的表面积s与半径r之间的函数关系式。
3、已知一个矩形的周长为12 m，设一边长为x m，面积为y ㎡，写出y与x之间的函数关系式。
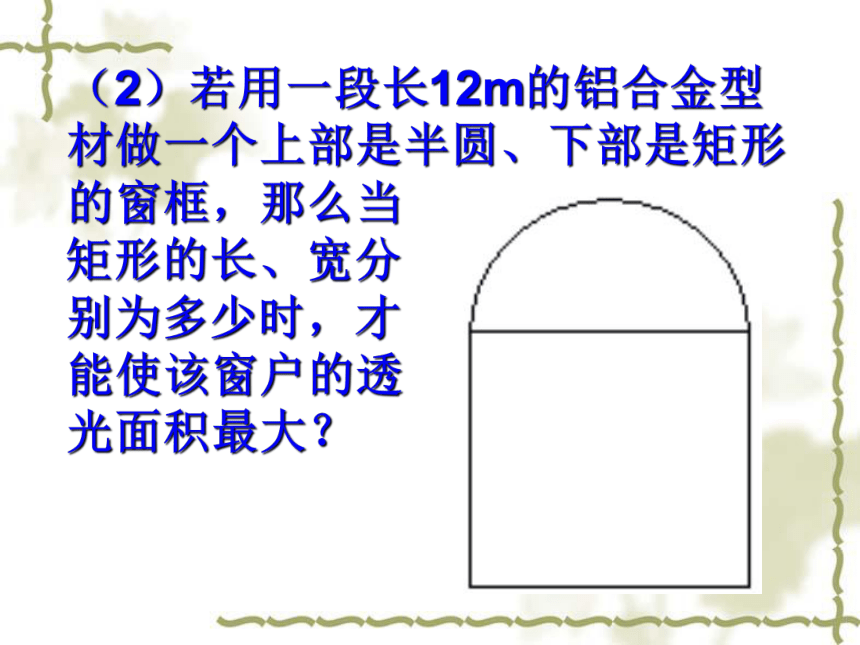
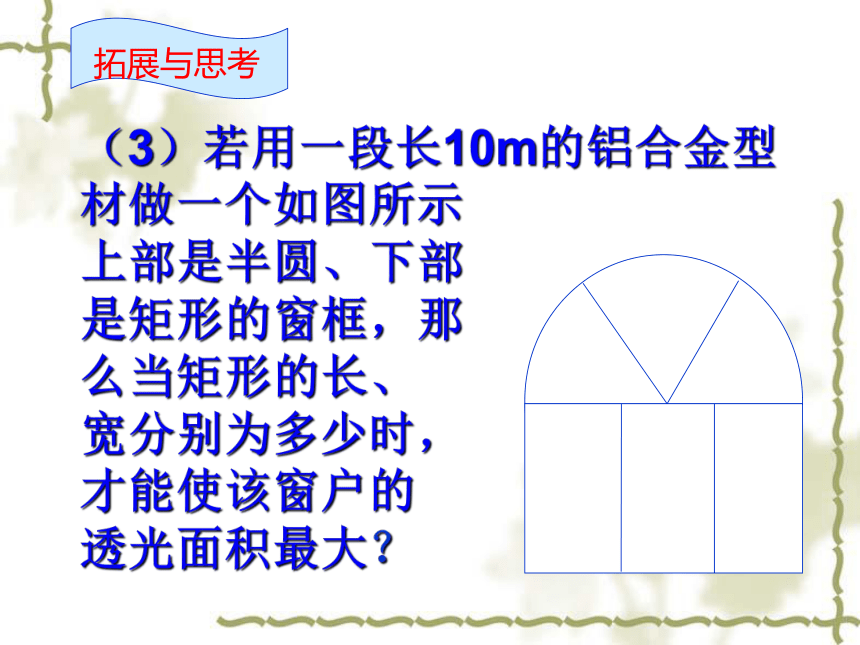
y=6x2 y=4∏r2 y=x(6-x)课前热身（1）若用一段长12m的铝合金型材做一个如图所示的矩形窗框，那么当矩形的长、宽分别为多少时，才能使该窗户的透光面积最大？发挥 你的聪明才智（2）若用一段长12m的铝合金型材做一个上部是半圆、下部是矩形的窗框，那么当矩形的长、宽分别为多少时，才能使该窗户的透光面积最大？（3）若用一段长10m的铝合金型材做一个如图所示上部是半圆、下部是矩形的窗框，那么当矩形的长、宽分别为多少时，才能使该窗户的透光面积最大？拓展与思考解:设窗户上半部半圆的半径为x(m),下半部矩形的宽为y(m),窗户面积为s 则:xy∵-3＜0, ∴窗户面积有最大值.当答:略. 如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。(1)求S与x的函数关系式及自变量的取值范围；(2)当x取何值时所围成的花圃面积最大，最大值是多少？(3)若墙的最大可用长度为8米，
则求围成花圃的最
大面积。 练习: 某经销店为某厂代销一种建材，当每吨售价为260元时，月销售量为45吨，该经销店为了提高经营利润，准备采取降价的方式进行促销，经调查发现，当每吨售价每下降10元时，月销售量就会增加7.5吨，综合考虑各种因素，每售出一吨建材共需支付厂家及其它费用100元，设每吨材料售价为x（元）该经销店的利润为y（元）(1)、当240元/吨，计算此时的月销售量；（2）求出y与x的函数关系式，（不要求写出x的取值范围）（3）该经销店要获得最大月利润，售价应定为每吨多少元？（4）小静说：当月利润最大时，月销售额也最大，你认为对吗？请说明理由。点拨：总利润=单个利润×总销售量，再利用配方法求出最大利润。解：（1）、（2）、巩固练习：课本第２６页１、２。　　如图，将一块半径为R的半圆形钢板切割成一个等腰梯形ABCD，已知AB是半圆的直径，点C、D在半圆上。
（1）试写出等腰梯形ABCD的周长y与腰长x之间的函数关系式；
（2）求梯形周长的
最大值，并求此时
梯形的面积。思考题 学了本节课你有什么收获和困惑？再见!