幂的乘方[上学期]
图片预览



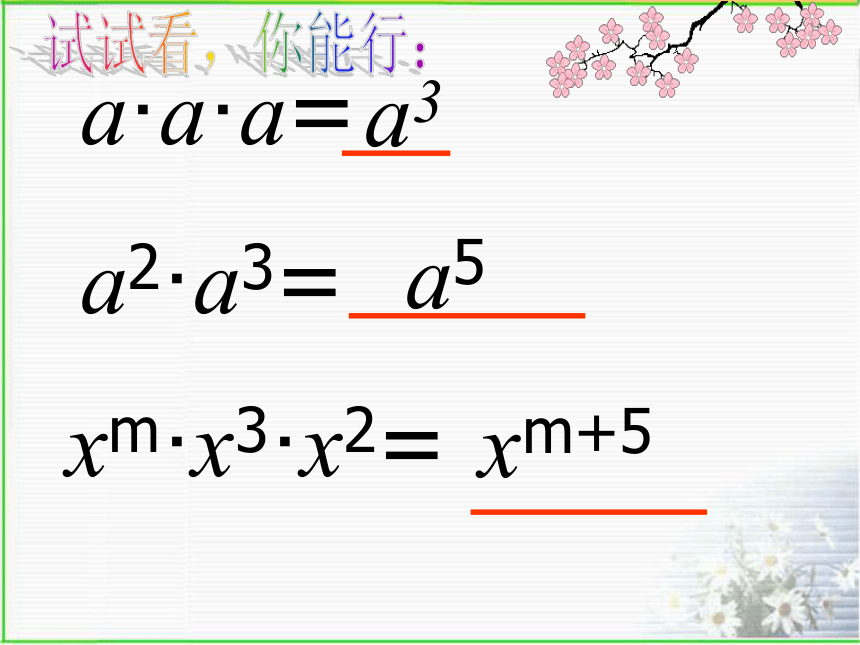








文档简介
课件30张PPT。15.2.2幂的乘方课前复习:同底数幂的乘法:
am · an = am+n (m、n为正整数) 练 习am+ma9a2·a3=a5xm·x3·x2=xm+5试试看,你能行:a·a·a=a322·(-2)3=-25xm·x3+xm+1·x2=2xm+3试试看,你能行:9·27 ·81=3Xx=93m=a则9a试试看,你能行:3m+2=xm=3, xn=5则xm+n=15根据 意义和同底数幂的乘法法则填空:乘方求几个相同因数的积的运算探索思考2.幂的乘方{{探究:幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则想一想读作:a的m次幂的n次方例1 计算:解:练习:计算⑴(23m)2⑵ (a2m)3n⑶ (a2m+1)5 猜一猜,试一试:看谁答得快! (24)3= (5) (-a3)2=
(2) (a5)3= (6) (-a2)3=
(3) [ (-3)5 ]2= (7) [(1-2b)3]3=
(4) [ (-a)3 ]5= (8) [ (a3)2 ]4=212a15310a6-a6a24-a15(1-2b)9多重乘方:小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .××练习:下面的式子成立吗?如果不对,应怎样改正?(1)(2)(3)√×××抢答题例2.计算下列各式,结果用幂的形式表示:(1)幂的乘方,底数不变,指数相乘。
(2)同底数幂的相乘,底数不变,指数相加。看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) (-b3)m=(-bm)3 ( )
× × × × ×下面的计算对吗?错的请改正 × × √ × × ×变一变,试试看
⑴ 85=2( )⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注:幂运算性质 均可逆向应用am·an=am+n(am) n=am n15469 解: ⑴x2·x4+(x3)2 =⑴x2·x4+(x3)2 ⑵(a3)3· (a4)3X2+4+x3×2=x6+x6=2x6能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.
3、若(-2)2 · 24= (a3)2,则a=______
8672动脑筋!±2思考题 4、我们知道,(an)m=(am)n,你能
根据这个结论计算 的值吗?动脑筋!幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10
(2)a2m =( )2 =( )m (m为正整数)
20x4x5 x2 ama2幂的乘方法则的逆用:www.czsx.com.cn想一想比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311444 =(44)11 = 25611 533 =(53)11 = 12511∴ 444 >355 > 533 在255,344,433,522,这四个幂的数值中,最大的一个是_______ 344智能挑战已知am=2,an=3. (m、n是正整数)勇攀高峰求下列各式的值
⑴a3m=
⑵a2n=
⑶a3m+2n=
⑷a3m+a2n=(胜利一定
属于我们)本节课的收获??相加相乘不变
不变
am · an = am+n (m、n为正整数) 练 习am+ma9a2·a3=a5xm·x3·x2=xm+5试试看,你能行:a·a·a=a322·(-2)3=-25xm·x3+xm+1·x2=2xm+3试试看,你能行:9·27 ·81=3Xx=93m=a则9a试试看,你能行:3m+2=xm=3, xn=5则xm+n=15根据 意义和同底数幂的乘法法则填空:乘方求几个相同因数的积的运算探索思考2.幂的乘方{{探究:幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则想一想读作:a的m次幂的n次方例1 计算:解:练习:计算⑴(23m)2⑵ (a2m)3n⑶ (a2m+1)5 猜一猜,试一试:看谁答得快! (24)3= (5) (-a3)2=
(2) (a5)3= (6) (-a2)3=
(3) [ (-3)5 ]2= (7) [(1-2b)3]3=
(4) [ (-a)3 ]5= (8) [ (a3)2 ]4=212a15310a6-a6a24-a15(1-2b)9多重乘方:小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .××练习:下面的式子成立吗?如果不对,应怎样改正?(1)(2)(3)√×××抢答题例2.计算下列各式,结果用幂的形式表示:(1)幂的乘方,底数不变,指数相乘。
(2)同底数幂的相乘,底数不变,指数相加。看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) (-b3)m=(-bm)3 ( )
× × × × ×下面的计算对吗?错的请改正 × × √ × × ×变一变,试试看
⑴ 85=2( )⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注:幂运算性质 均可逆向应用am·an=am+n(am) n=am n15469 解: ⑴x2·x4+(x3)2 =⑴x2·x4+(x3)2 ⑵(a3)3· (a4)3X2+4+x3×2=x6+x6=2x6能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.
3、若(-2)2 · 24= (a3)2,则a=______
8672动脑筋!±2思考题 4、我们知道,(an)m=(am)n,你能
根据这个结论计算 的值吗?动脑筋!幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10
(2)a2m =( )2 =( )m (m为正整数)
20x4x5 x2 ama2幂的乘方法则的逆用:www.czsx.com.cn想一想比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311444 =(44)11 = 25611 533 =(53)11 = 12511∴ 444 >355 > 533 在255,344,433,522,这四个幂的数值中,最大的一个是_______ 344智能挑战已知am=2,an=3. (m、n是正整数)勇攀高峰求下列各式的值
⑴a3m=
⑵a2n=
⑶a3m+2n=
⑷a3m+a2n=(胜利一定
属于我们)本节课的收获??相加相乘不变
不变
