湖南省长沙市2022-2023学年八年级下学期期末考试数学试题(无答案)
文档属性
| 名称 | 湖南省长沙市2022-2023学年八年级下学期期末考试数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 197.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 12:35:34 | ||
图片预览

文档简介
2022-2023学年第二学期期末考试
初二 数学
时量:120分钟 总分:120分
一、选择题(每小题3分,共30分)
1.2023的相反数是( )
A.2023 B. C. D.
2.下列各式计算正确的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.了解市民知晓“礼让行人”交通新规的情况,适合全面调查
B.一组数据5,5,3,4,1的中位数是3
C.一组数据中出现次数最多的数是这组数据的众数
D.甲、乙两人9次跳高成绩的方差分别为,,说明乙的成绩比甲稳定
4.国家统计局统计数据显示,我国快递业务逐年增加,2020年至2022年我国快递业务收入由7500亿元增加到9000亿元.设我国2020年至2022年快递业务收入的年平均增长率为x,则可列方程为( )
A. B.
C. D.
5.对于函数,说法正确的是( )
A.点在这个函数图象上 B.y随着x的增大而增大
C.它的图象必过一、三象限 D.当时,
6.如图,在中,,对角线AC与BD相交于点O,,则△BOC的周长为( )
A.10 B.11 C.12 D.14
第6题图 第8题图
7.将抛物线向左平移1个单位长度,再向下平移4个单位长度,得到抛物线为( )
A. B.
C. D.
8.已知实心球运动的高度与水平距离之间的函数关系是,则该同学此次投掷实心球的成绩是( )
A.2m B.3m C.3.5m D.4m
9.已知a,b是一元二次方程的两个实数根,则代数式的值等于( )
A.7 B.8 C.9 D.10
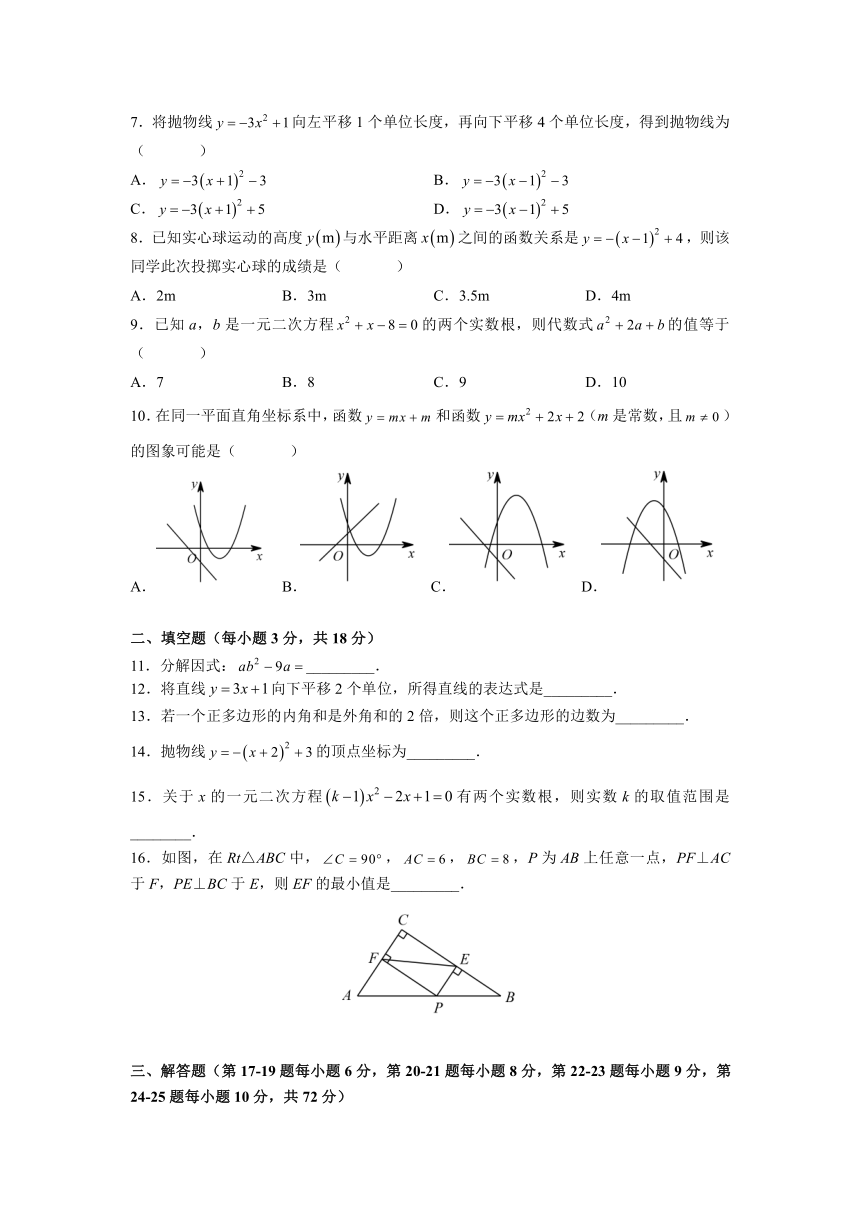
10.在同一平面直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A. B.C.D.
二、填空题(每小题3分,共18分)
11.分解因式:_________.
12.将直线向下平移2个单位,所得直线的表达式是_________.
13.若一个正多边形的内角和是外角和的2倍,则这个正多边形的边数为_________.
14.抛物线的顶点坐标为_________.
15.关于x的一元二次方程有两个实数根,则实数k的取值范围是________.
16.如图,在Rt△ABC中,,,,P为AB上任意一点,PF⊥AC于F,PE⊥BC于E,则EF的最小值是_________.
三、解答题(第17-19题每小题6分,第20-21题每小题8分,第22-23题每小题9分,第24-25题每小题10分,共72分)
17.计算:.
18.先化简,再求值:,其中.
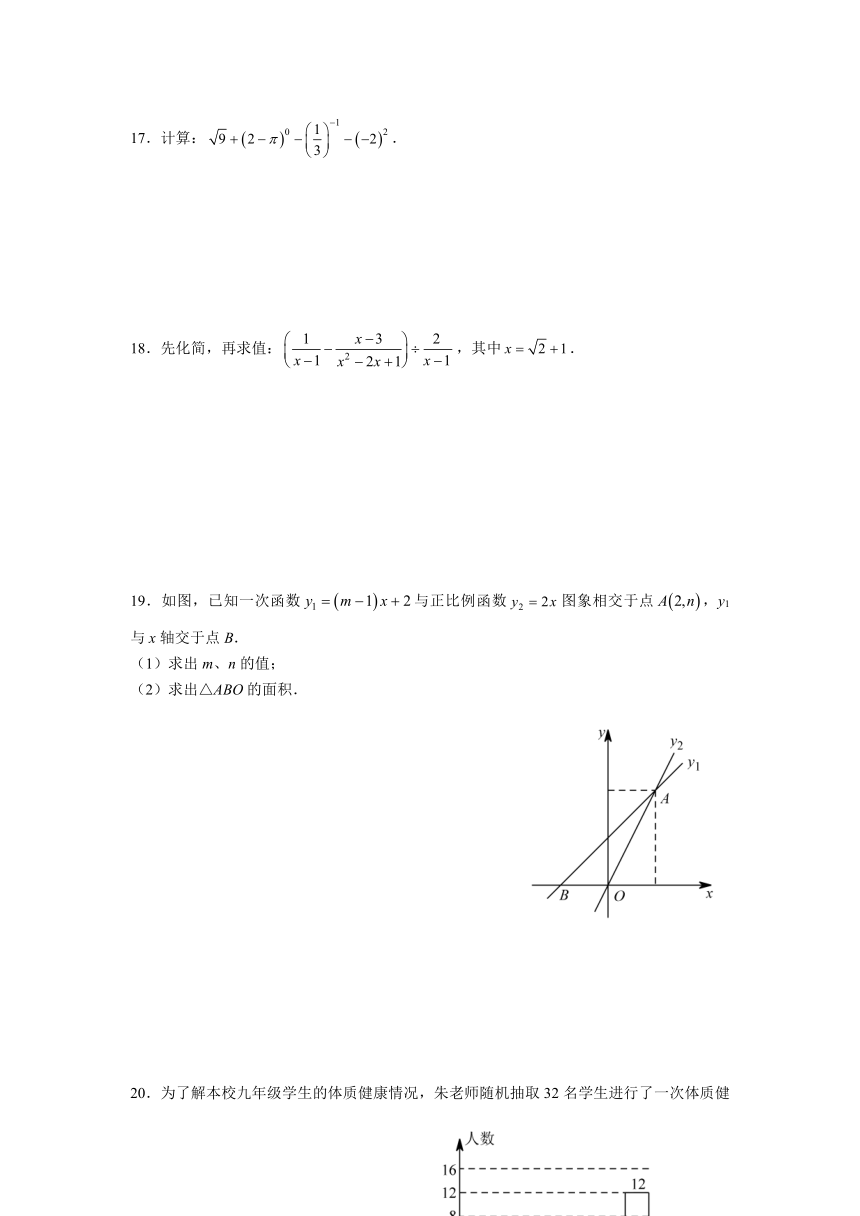
19.如图,已知一次函数与正比例函数图象相交于点,y1与x轴交于点B.
(1)求出m、n的值;
(2)求出△ABO的面积.
20.为了解本校九年级学生的体质健康情况,朱老师随机抽取32名学生进行了一次体质健康测试,规定分数在75分(包含75分)以上为良好;根据测试成绩制成统计图表.
组别 分数段 人数
A 2
B 5
C a
D 12
请根据上述信息解答下列问题:
(1)本次调查中的样本容量是________,________;
(2)补全条形统计图;
(3)样本数据的中位数位于________组;
(4)该校九年级学生有960人,估计该校九年级学生体质健康测试成绩为良好的有多少人?
21.如图,,,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:;
(2)若,,求BE的长.
22.近几年,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)满足关系式,设销售这种商品每天的利润为W(元).
(1)求W与x之间的函数关系式;
(2)当销售单价不低于28元,且每天至少销售50件时,求W的最大值.
23.如图,在Rt△ABC中,,,D是AC的中点,过点D作DE⊥AC交BC于点E,延长ED至F,使,连接AE,AF,CF.
(1)求证:四边形AECF是菱形;
(2)若,,求EF的长.
24.定义:我们不妨把纵坐标是横坐标2倍的点称为“青竹点”.例如:点、……都是“青竹点”.显然,函数的图像上有两个“青竹点”:和.
(1)下列函数中,函数图像上存在“青竹点”的,请在横线上打“√”,不存在“青竹点”的,请打“×”.
①________; ②________; ③________.
(2)若抛物线(m为常数)上存在两个不同的“青竹点”,求m的取值范围;
(3)若函数的图像上存在唯一的一个“青竹点”,且当时,a的最小值为c,求c的值.
25.如图,在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,且.
(1)求抛物线的解析式;
(2)如图①,若点P为第一象限的抛物线上一点,直线CP交x轴于点D,且CP平分∠OCB,求点P的坐标;
(3)如图②,点Q为第四象限的抛物线上一点,直线BQ交y轴于点M,过点B作直线NB∥AQ,交y轴于点N,当Q点运动时,线段MN的长度是否会变化?若不变,请求出其长度;若变化,请求出其长度的变化范围.
图① 图②
初二 数学
时量:120分钟 总分:120分
一、选择题(每小题3分,共30分)
1.2023的相反数是( )
A.2023 B. C. D.
2.下列各式计算正确的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.了解市民知晓“礼让行人”交通新规的情况,适合全面调查
B.一组数据5,5,3,4,1的中位数是3
C.一组数据中出现次数最多的数是这组数据的众数
D.甲、乙两人9次跳高成绩的方差分别为,,说明乙的成绩比甲稳定
4.国家统计局统计数据显示,我国快递业务逐年增加,2020年至2022年我国快递业务收入由7500亿元增加到9000亿元.设我国2020年至2022年快递业务收入的年平均增长率为x,则可列方程为( )
A. B.
C. D.
5.对于函数,说法正确的是( )
A.点在这个函数图象上 B.y随着x的增大而增大
C.它的图象必过一、三象限 D.当时,
6.如图,在中,,对角线AC与BD相交于点O,,则△BOC的周长为( )
A.10 B.11 C.12 D.14
第6题图 第8题图
7.将抛物线向左平移1个单位长度,再向下平移4个单位长度,得到抛物线为( )
A. B.
C. D.
8.已知实心球运动的高度与水平距离之间的函数关系是,则该同学此次投掷实心球的成绩是( )
A.2m B.3m C.3.5m D.4m
9.已知a,b是一元二次方程的两个实数根,则代数式的值等于( )
A.7 B.8 C.9 D.10
10.在同一平面直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A. B.C.D.
二、填空题(每小题3分,共18分)
11.分解因式:_________.
12.将直线向下平移2个单位,所得直线的表达式是_________.
13.若一个正多边形的内角和是外角和的2倍,则这个正多边形的边数为_________.
14.抛物线的顶点坐标为_________.
15.关于x的一元二次方程有两个实数根,则实数k的取值范围是________.
16.如图,在Rt△ABC中,,,,P为AB上任意一点,PF⊥AC于F,PE⊥BC于E,则EF的最小值是_________.
三、解答题(第17-19题每小题6分,第20-21题每小题8分,第22-23题每小题9分,第24-25题每小题10分,共72分)
17.计算:.
18.先化简,再求值:,其中.
19.如图,已知一次函数与正比例函数图象相交于点,y1与x轴交于点B.
(1)求出m、n的值;
(2)求出△ABO的面积.
20.为了解本校九年级学生的体质健康情况,朱老师随机抽取32名学生进行了一次体质健康测试,规定分数在75分(包含75分)以上为良好;根据测试成绩制成统计图表.
组别 分数段 人数
A 2
B 5
C a
D 12
请根据上述信息解答下列问题:
(1)本次调查中的样本容量是________,________;
(2)补全条形统计图;
(3)样本数据的中位数位于________组;
(4)该校九年级学生有960人,估计该校九年级学生体质健康测试成绩为良好的有多少人?
21.如图,,,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:;
(2)若,,求BE的长.
22.近几年,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)满足关系式,设销售这种商品每天的利润为W(元).
(1)求W与x之间的函数关系式;
(2)当销售单价不低于28元,且每天至少销售50件时,求W的最大值.
23.如图,在Rt△ABC中,,,D是AC的中点,过点D作DE⊥AC交BC于点E,延长ED至F,使,连接AE,AF,CF.
(1)求证:四边形AECF是菱形;
(2)若,,求EF的长.
24.定义:我们不妨把纵坐标是横坐标2倍的点称为“青竹点”.例如:点、……都是“青竹点”.显然,函数的图像上有两个“青竹点”:和.
(1)下列函数中,函数图像上存在“青竹点”的,请在横线上打“√”,不存在“青竹点”的,请打“×”.
①________; ②________; ③________.
(2)若抛物线(m为常数)上存在两个不同的“青竹点”,求m的取值范围;
(3)若函数的图像上存在唯一的一个“青竹点”,且当时,a的最小值为c,求c的值.
25.如图,在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,且.
(1)求抛物线的解析式;
(2)如图①,若点P为第一象限的抛物线上一点,直线CP交x轴于点D,且CP平分∠OCB,求点P的坐标;
(3)如图②,点Q为第四象限的抛物线上一点,直线BQ交y轴于点M,过点B作直线NB∥AQ,交y轴于点N,当Q点运动时,线段MN的长度是否会变化?若不变,请求出其长度;若变化,请求出其长度的变化范围.
图① 图②
同课章节目录
