人教版数学八年级上册 14.2.1 平方差公式 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.2.1 平方差公式 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 22:53:27 | ||
图片预览





文档简介
(共19张PPT)
14.2.1平方差公式
14.2 乘法公式
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
5米
5米
a米
(a-5)
(a+5)米
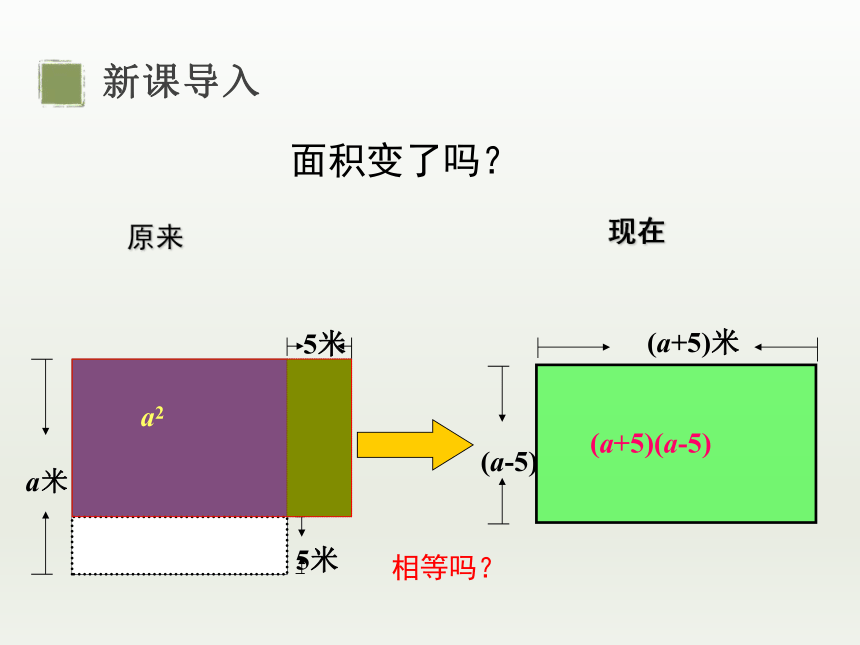
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
新课导入
讲授新知
贰
计算下列多项式的积:
(1) (x+1)(x-1)=_________=_____;
(2) (m+2)(m-2)=_____________=_____;
(3) (2x+1)(2x-1)=_____________=______.
x·x-x+x-1
x2 -1
m·m-2m+2m-4
m2 -4
= m2 -22
2x·2x-2x+2x-1
4x2 -1
=(2x)2 -12
观察计算结果,你能发现什么规律?
=x2 -12
猜想:(a+b)(a-b)= .
a2 -b2
如何证明这个等式呢?
知识点1 平方差公式
讲授新知
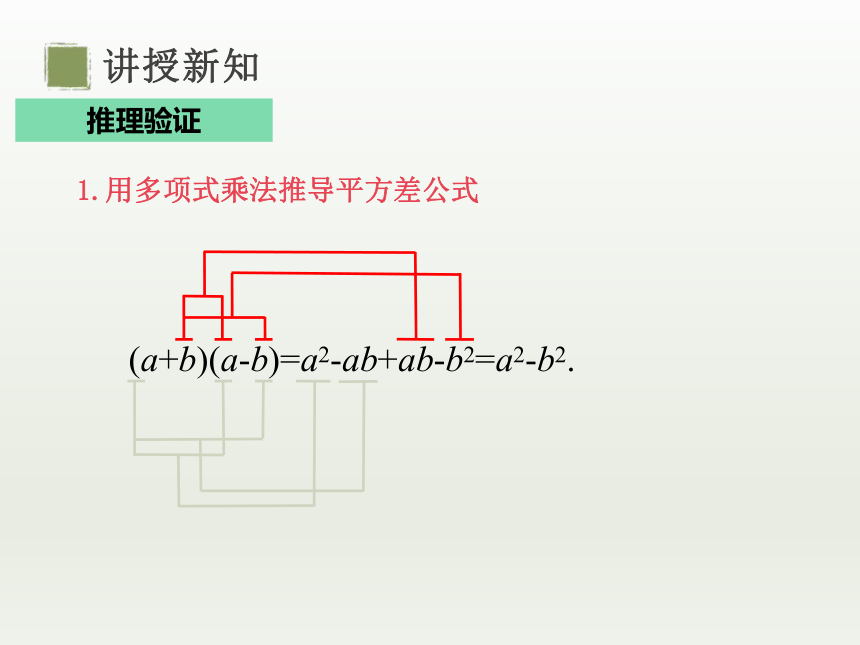
1.用多项式乘法推导平方差公式
(a+b)(a-b)=a2-ab+ab-b2=a2-b2.
讲授新知
推理验证
2.借助几何图形推导平方差公式
图中有两个边长分别为a,b的正方形,两个正方形的面积之差可以表示为a2- b2.
b
a
a-b
b
将图中右下方的长方形移动位置后,拼得一个长为(a+b),宽为(a-b)
的长方形,其面积为
(a+b)(a-b).
(a+b)(a-b)=a2-b2.
讲授新知
平方差公式:
(a+b)(a-b)=a2-b2.
特点:(1) 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
(2) 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方.
两个数的和
两个数的差
积
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
讲授新知
a
b
b2
a2
(4x+3)(4x-3)=(4x)2-32=16x2-9.
平方差公式计算的示例:
注意:(1) 平方差公式的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2) 在运用公式时,要分清楚哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
讲授新知
例1 运用平方差公式计算:
(1) (3x+2)(3x-2); (2) (-x+2y)(-x-2y) .
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2 .
分析:(1) 3x相当于a,2相当于b.
(2) -x相当于a,2y相当于b.
范例应用
例2 计算:
(1) (y+2)(y-2)-(y-1)(y+5); (2) 102×98.
解:(1) (y+2)(y-2)-(y-1)(y+5)
=y2-22-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1;
(2) 102×98
=(100+2)(100-2)
=1002-22
=9 996.
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
范例应用
当堂训练
叁
当堂训练
1.下列各式中不能用平方差公式计算的是( )
A.(m-n)(-m-n) B.(x3-y3)(y3+x3)
C.(-m+n)(m-n) D.(2x-3)(3+2x)
2.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.( 0.1a+b)(b- 0.1 a)
C.(-a+b)(a-b) D.(x2-y)(x+y2)
3.用平方差公式计算(x+1)(x-1)(x2+1)的结果正确的是( )
A.x4-1 B.x4+1 C.(x-1)4 D.(x+1)4
4.对于任意整数m,能整除代数式(m+3)(m-3)-(m-2)(m+2)的整数是( )A.4 B.3 C.5 D. 2
C
B
A
C
(
(1)(3a+2b)(3a-2b) (2)(-3x-5y)(-3x+5y)
(3)101×99 (4)(a-b)(a+b)(a2+b2)
5.用平方差公式计算:
(2)(-3x-5y)(-3x+5y)=(-3x)2-(5y)2=9x2-25y2;
解:(1)(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2;
(3)101×99=(100+1)(100-1)=1002-1=10000-1=9999;
(4)(a-b)(a+b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
课堂小结
肆
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
课堂小结
课后作业
基础题:1.课后练习 P108第 1,2题。
提高题:2.请学有余力的同学做同步训练
谢
谢
14.2.1平方差公式
14.2 乘法公式
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
新课导入
讲授新知
贰
计算下列多项式的积:
(1) (x+1)(x-1)=_________=_____;
(2) (m+2)(m-2)=_____________=_____;
(3) (2x+1)(2x-1)=_____________=______.
x·x-x+x-1
x2 -1
m·m-2m+2m-4
m2 -4
= m2 -22
2x·2x-2x+2x-1
4x2 -1
=(2x)2 -12
观察计算结果,你能发现什么规律?
=x2 -12
猜想:(a+b)(a-b)= .
a2 -b2
如何证明这个等式呢?
知识点1 平方差公式
讲授新知
1.用多项式乘法推导平方差公式
(a+b)(a-b)=a2-ab+ab-b2=a2-b2.
讲授新知
推理验证
2.借助几何图形推导平方差公式
图中有两个边长分别为a,b的正方形,两个正方形的面积之差可以表示为a2- b2.
b
a
a-b
b
将图中右下方的长方形移动位置后,拼得一个长为(a+b),宽为(a-b)
的长方形,其面积为
(a+b)(a-b).
(a+b)(a-b)=a2-b2.
讲授新知
平方差公式:
(a+b)(a-b)=a2-b2.
特点:(1) 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
(2) 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方.
两个数的和
两个数的差
积
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
讲授新知
a
b
b2
a2
(4x+3)(4x-3)=(4x)2-32=16x2-9.
平方差公式计算的示例:
注意:(1) 平方差公式的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2) 在运用公式时,要分清楚哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
讲授新知
例1 运用平方差公式计算:
(1) (3x+2)(3x-2); (2) (-x+2y)(-x-2y) .
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2 .
分析:(1) 3x相当于a,2相当于b.
(2) -x相当于a,2y相当于b.
范例应用
例2 计算:
(1) (y+2)(y-2)-(y-1)(y+5); (2) 102×98.
解:(1) (y+2)(y-2)-(y-1)(y+5)
=y2-22-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1;
(2) 102×98
=(100+2)(100-2)
=1002-22
=9 996.
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
范例应用
当堂训练
叁
当堂训练
1.下列各式中不能用平方差公式计算的是( )
A.(m-n)(-m-n) B.(x3-y3)(y3+x3)
C.(-m+n)(m-n) D.(2x-3)(3+2x)
2.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.( 0.1a+b)(b- 0.1 a)
C.(-a+b)(a-b) D.(x2-y)(x+y2)
3.用平方差公式计算(x+1)(x-1)(x2+1)的结果正确的是( )
A.x4-1 B.x4+1 C.(x-1)4 D.(x+1)4
4.对于任意整数m,能整除代数式(m+3)(m-3)-(m-2)(m+2)的整数是( )A.4 B.3 C.5 D. 2
C
B
A
C
(
(1)(3a+2b)(3a-2b) (2)(-3x-5y)(-3x+5y)
(3)101×99 (4)(a-b)(a+b)(a2+b2)
5.用平方差公式计算:
(2)(-3x-5y)(-3x+5y)=(-3x)2-(5y)2=9x2-25y2;
解:(1)(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2;
(3)101×99=(100+1)(100-1)=1002-1=10000-1=9999;
(4)(a-b)(a+b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
课堂小结
肆
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
课堂小结
课后作业
基础题:1.课后练习 P108第 1,2题。
提高题:2.请学有余力的同学做同步训练
谢
谢
