北师大版七年级上册数学第一章丰富的图形世界测试题(含答案)
文档属性
| 名称 | 北师大版七年级上册数学第一章丰富的图形世界测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 16:54:26 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版七年级上册数学第一章测试题(附答案)
一、单选题(共12题;共36分)
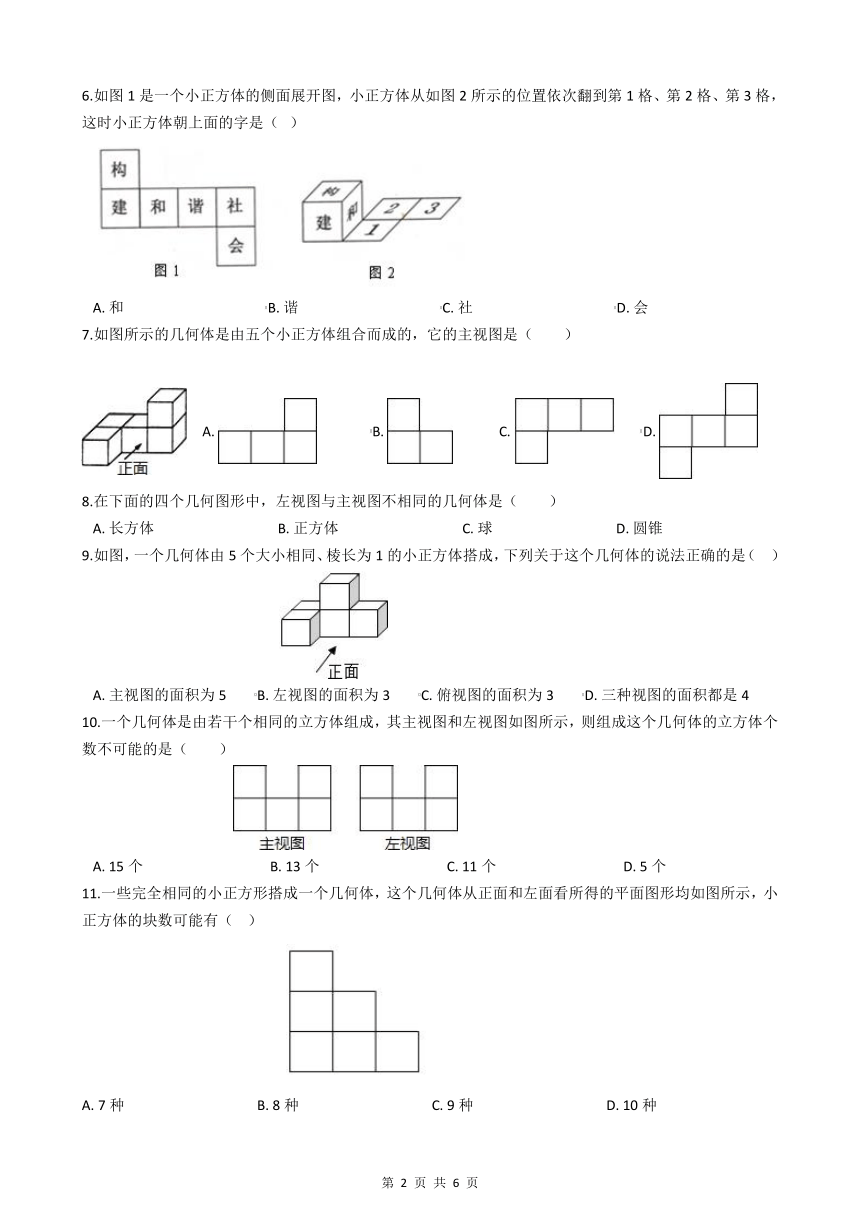
1.如图,有一个正方体,乐乐用了一个平面去截这个正方体,截面形状不可能是( )
A. B. C. D.
2.如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )
A. B. C. D.
3.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B. 正方体 C. 球 D. 圆锥
4.如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )
A. B. C. D.
5.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( )
A. B. C. D.
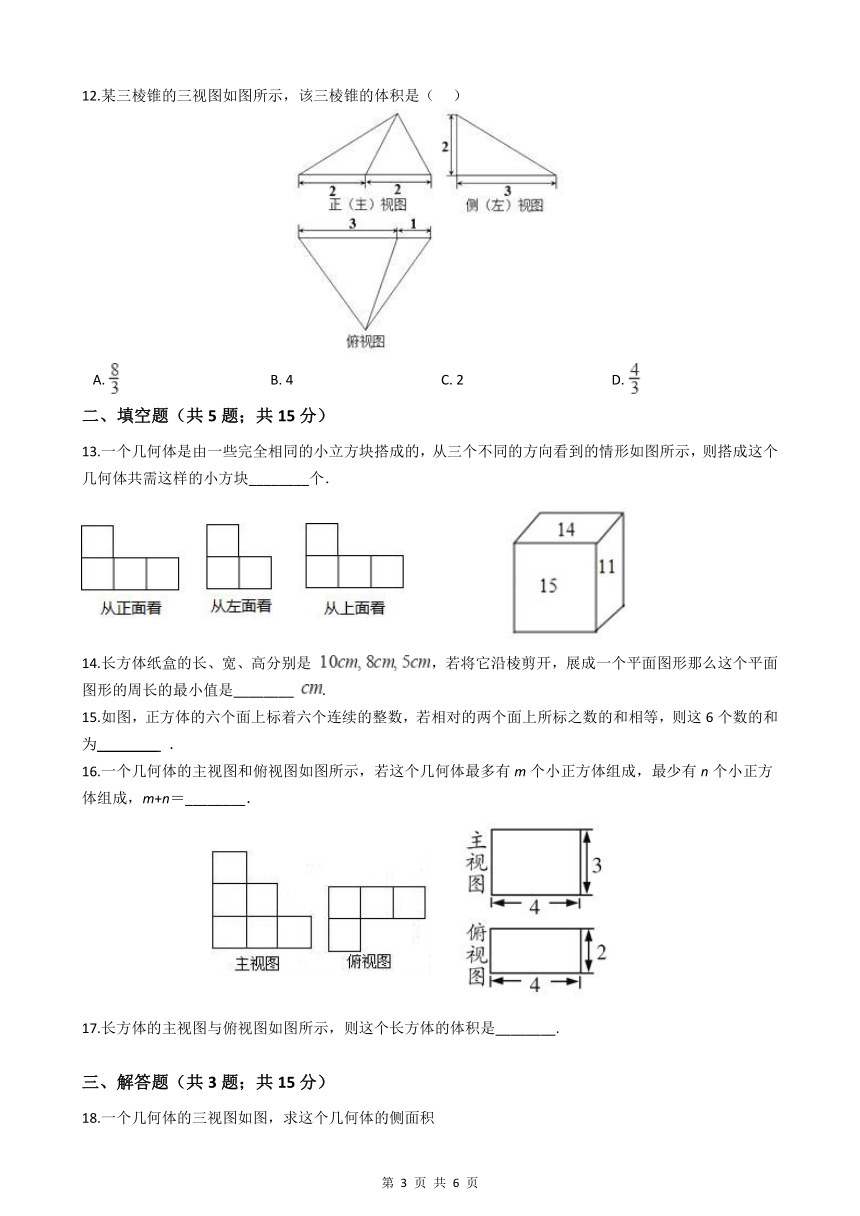
6.如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( )
A. 和 B. 谐 C. 社 D. 会
7.如图所示的几何体是由五个小正方体组合而成的,它的主视图是( )
A. B. C. D.
8.在下面的四个几何图形中,左视图与主视图不相同的几何体是( )
A. 长方体 B. 正方体 C. 球 D. 圆锥
9.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
A. 主视图的面积为5 B. 左视图的面积为3 C. 俯视图的面积为3 D. 三种视图的面积都是4
10.一个几何体是由若干个相同的立方体组成,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是( )
A. 15个 B. 13个 C. 11个 D. 5个
11.一些完全相同的小正方形搭成一个几何体,这个几何体从正面和左面看所得的平面图形均如图所示,小正方体的块数可能有( )
A. 7种 B. 8种 C. 9种 D. 10种
12.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B. 4 C. 2 D.
二、填空题(共5题;共15分)
13.一个几何体是由一些完全相同的小立方块搭成的,从三个不同的方向看到的情形如图所示,则搭成这个几何体共需这样的小方块________个.
14.长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是________ .
15.如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为________ .
16.一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,m+n=________.
17.长方体的主视图与俯视图如图所示,则这个长方体的体积是________.
三、解答题(共3题;共15分)
18.一个几何体的三视图如图,求这个几何体的侧面积
19.长方体的主视图与俯视图如图所示,这个长方体的体积是多少?
20.如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 , 那么S1与S的大小关系是
A.S1>S B.S1=S C.S1<S D.无法确定
(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1 , 那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.
四、作图题(共1题;共8分)
21.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
五、综合题(共2题;共26分)
22.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有________.
(2)从已知正确的纸样中选出一种,在原图上标注上尺寸.
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
23.如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的上面,那么哪一面会在下面
(2)如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面
答案
一、单选题
1. D 2. D 3. D 4. B 5. C 6. D 7. A 8. A 9. B 10. A 11. C 12.B
二、填空题
13. 5 14. 92 15. 8116. 16 17. 24
三、解答题
18. 解:根据三视图可得:这个几何体是圆柱,
∵圆柱的直径为2,高为3,∴侧面积为2×""×2×3π=6π.
答:这个几何体的侧面积是6π.
19. 解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,
因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24.
答:这个长方体的体积是24.
20. 解:(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 ,
那么S1与S的大小关系是相等;故选:B;
(2)设大正方体棱长为1,小正方体棱长为x,那么l1﹣l=6x.
只有当x= 时,才有6x=3,所以小明的话是不对的;
(3)如图所示:
四、作图题
21. 解:如图所示:
五、综合题
22. (1)甲.丙;(2)标注尺寸只需在甲图或丙图标出一种即可
(3)S侧=(b+a+b+a)h=2ah+2bh;S表=S侧+2S底=2ah+2bh+2ab .
23. (1)解:如果面A在多面体的上面,那么C面会在下面
(2)解:如果面在多面体的后面,从左面看是面C,那么向外折时面C会在上面,向里折时面A会在上面。
(3)解:从右面看是面A,从上面看是面E,那么向外这时从前面看是面B,向里折时从前面看是面D。
(
第
- 1 -
页 共
8
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版七年级上册数学第一章测试题(附答案)
一、单选题(共12题;共36分)
1.如图,有一个正方体,乐乐用了一个平面去截这个正方体,截面形状不可能是( )
A. B. C. D.
2.如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )
A. B. C. D.
3.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B. 正方体 C. 球 D. 圆锥
4.如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )
A. B. C. D.
5.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( )
A. B. C. D.
6.如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( )
A. 和 B. 谐 C. 社 D. 会
7.如图所示的几何体是由五个小正方体组合而成的,它的主视图是( )
A. B. C. D.
8.在下面的四个几何图形中,左视图与主视图不相同的几何体是( )
A. 长方体 B. 正方体 C. 球 D. 圆锥
9.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
A. 主视图的面积为5 B. 左视图的面积为3 C. 俯视图的面积为3 D. 三种视图的面积都是4
10.一个几何体是由若干个相同的立方体组成,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是( )
A. 15个 B. 13个 C. 11个 D. 5个
11.一些完全相同的小正方形搭成一个几何体,这个几何体从正面和左面看所得的平面图形均如图所示,小正方体的块数可能有( )
A. 7种 B. 8种 C. 9种 D. 10种
12.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B. 4 C. 2 D.
二、填空题(共5题;共15分)
13.一个几何体是由一些完全相同的小立方块搭成的,从三个不同的方向看到的情形如图所示,则搭成这个几何体共需这样的小方块________个.
14.长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是________ .
15.如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为________ .
16.一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,m+n=________.
17.长方体的主视图与俯视图如图所示,则这个长方体的体积是________.
三、解答题(共3题;共15分)
18.一个几何体的三视图如图,求这个几何体的侧面积
19.长方体的主视图与俯视图如图所示,这个长方体的体积是多少?
20.如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 , 那么S1与S的大小关系是
A.S1>S B.S1=S C.S1<S D.无法确定
(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1 , 那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.
四、作图题(共1题;共8分)
21.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
五、综合题(共2题;共26分)
22.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有________.
(2)从已知正确的纸样中选出一种,在原图上标注上尺寸.
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
23.如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的上面,那么哪一面会在下面
(2)如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面
答案
一、单选题
1. D 2. D 3. D 4. B 5. C 6. D 7. A 8. A 9. B 10. A 11. C 12.B
二、填空题
13. 5 14. 92 15. 8116. 16 17. 24
三、解答题
18. 解:根据三视图可得:这个几何体是圆柱,
∵圆柱的直径为2,高为3,∴侧面积为2×""×2×3π=6π.
答:这个几何体的侧面积是6π.
19. 解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,
因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24.
答:这个长方体的体积是24.
20. 解:(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 ,
那么S1与S的大小关系是相等;故选:B;
(2)设大正方体棱长为1,小正方体棱长为x,那么l1﹣l=6x.
只有当x= 时,才有6x=3,所以小明的话是不对的;
(3)如图所示:
四、作图题
21. 解:如图所示:
五、综合题
22. (1)甲.丙;(2)标注尺寸只需在甲图或丙图标出一种即可
(3)S侧=(b+a+b+a)h=2ah+2bh;S表=S侧+2S底=2ah+2bh+2ab .
23. (1)解:如果面A在多面体的上面,那么C面会在下面
(2)解:如果面在多面体的后面,从左面看是面C,那么向外折时面C会在上面,向里折时面A会在上面。
(3)解:从右面看是面A,从上面看是面E,那么向外这时从前面看是面B,向里折时从前面看是面D。
(
第
- 1 -
页 共
8
页
)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
