26.3.1二次函数实践与探索[下学期]
文档属性
| 名称 | 26.3.1二次函数实践与探索[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 879.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-04 00:00:00 | ||
图片预览





文档简介
课件25张PPT。实践与探索26.3.1二次函数解析式的几种表达式 一般式:y=ax2+bx+c 顶点式:y=a(x-h)2+k 两根式:y=a(x-x1)(x-x2)1.已知二次函数的图象过
点(- 2,0),在y轴上的截距
为- 3,对称轴 x=2,求它的
解析式.练习2.抛物线y=x2-2(m-1)x+n过点(2,4),且其顶点在直线y=2x+1上,
(1)求这抛物线的解析式.
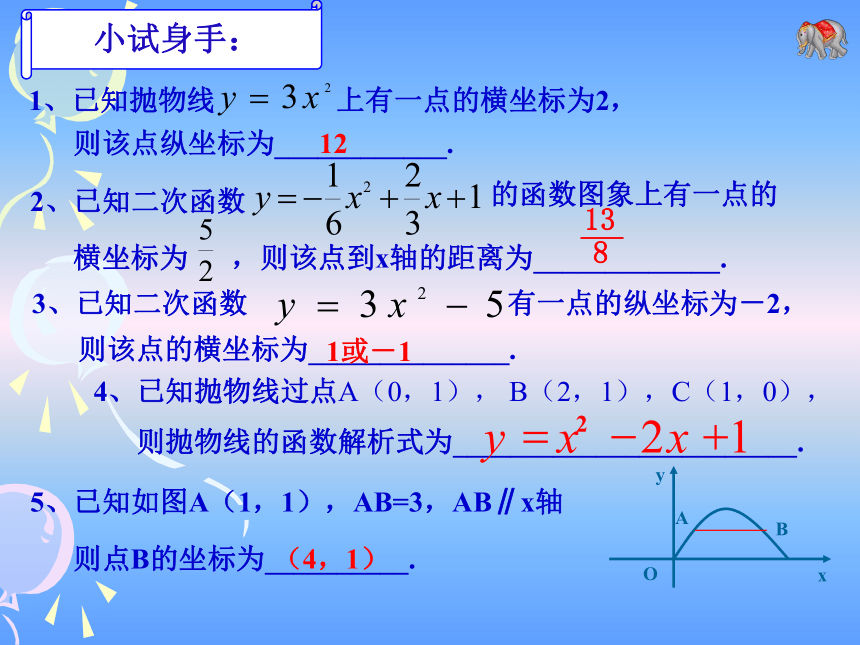
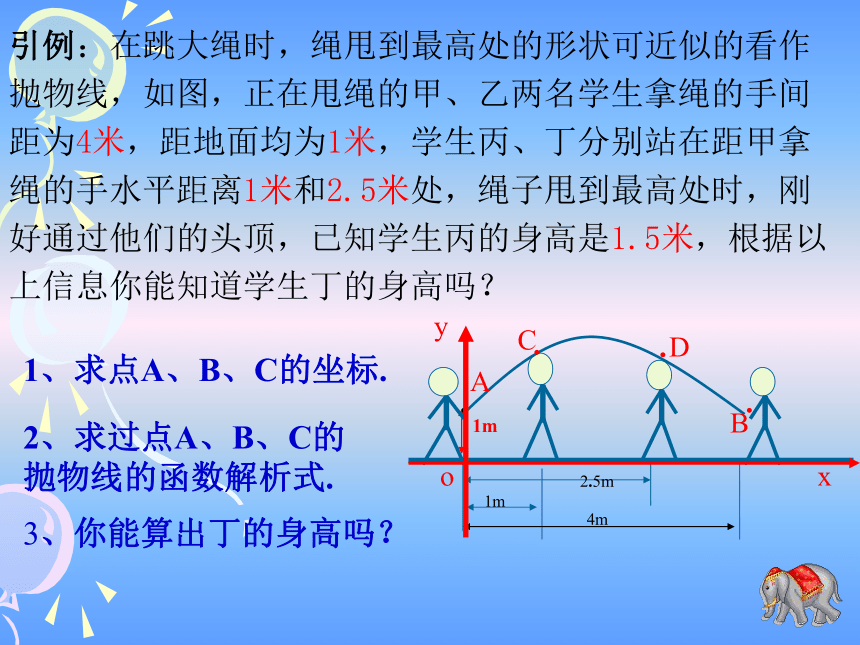
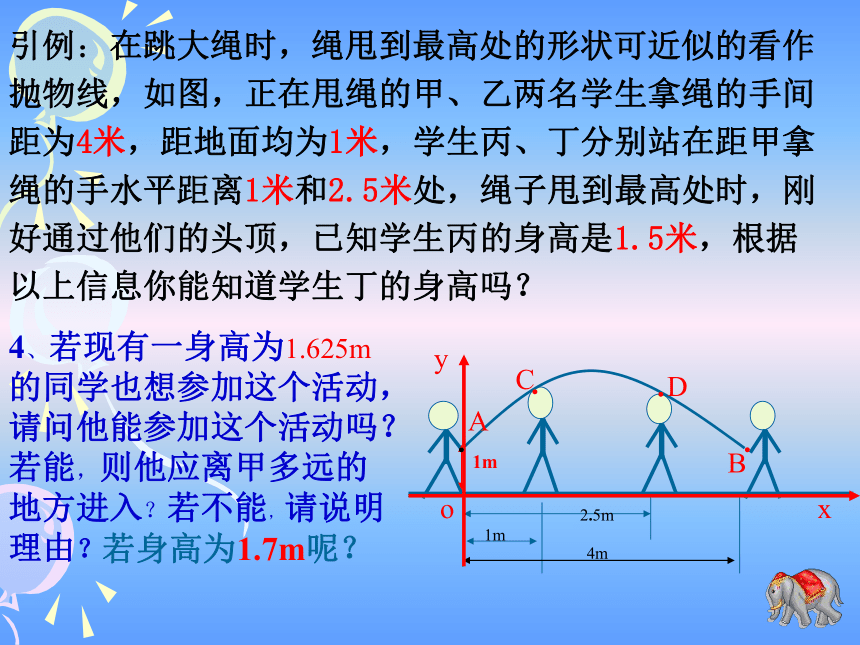
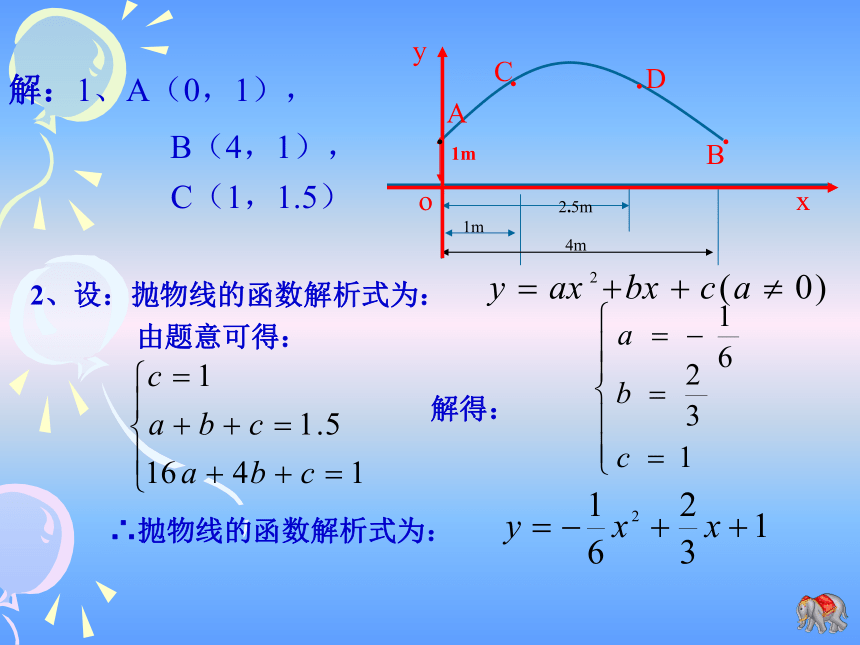
(2)求直线y=2x+1与抛物线的对称轴x轴所围成的三角形的面积.121或-15、已知如图A(1,1),AB=3,AB∥x轴OxyAB则点B的坐标为__________.(4,1)引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?1、求点A、B、C的坐标.2、求过点A、B、C的抛物线的函数解析式.3、你能算出丁的身高吗?引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?4、若现有一身高为1.625m的同学也想参加这个活动,请问他能参加这个活动吗?若能,则他应离甲多远的地方进入?若不能,请说明理由?若身高为1.7m呢?2、设:抛物线的函数解析式为:由题意可得:解得:∴抛物线的函数解析式为:∴该同学应该在离甲同学1.5m至2.5m处.例1.如图26.3.1,一位运动员推铅
球,铅球行进高度y(m)与水平距离x
(m)之间的关系是,问此运动员把铅球推出多远?解 如图,铅球落在x轴上,则y=0,
因此,解方程,得所以,此运动员把铅球推出了10米.(不合题意,舍去).例2.如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,点O是水池中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.(1)若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流最大高度应达多少米?(精确到0.1m).分析 这是一个运用抛物线的有关知识解决实际问题的应用题,首先必须将水流抛物线放在直角坐标系中,如图26.3.3,我们可以求出抛物线的函数关系式,再利用抛物线的性质即可解决问题. 确定二此函数的关系式的一般方法是待定系数法,在选择把二次函数的关系式设成什么形式时,可根据题目中的条件灵活选择,以简单为原则.二次函数的关系式可设如下二种形式:
(1)一般式:(2)顶点式:给出两点,且其中一点为顶点时可利用此式来求.给出三点坐标可利用此式来求.回顾与反思问题2 一个涵洞成抛物线形,它的截面如图.
现测得,当水面宽AB=1.6 m时,涵洞
顶点与水面的距离为2.4 m.这时,离
开水面1.5 m处,涵洞宽ED是多少?
是否会超过1 m?如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,
求(1)以这一部分抛物线
为图象的函数解析式,并写
出x的取值范围;
(2) 有一辆宽2.8米,高
1米的农用货车(货物最高
处与地面AB的距离)能否通
过此隧道?问题3画出 函数的图象,根据图象回答下列问题.
图象与x 轴交点的坐标是什么?
当x 取何值时,y=0?这里x的取值
与方程 有什么关系?(3)当x 取何值时,y<0?当x取何值时,y>0?
(4)能否用含有x的不等式来描述(3)
中的问题?1、抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点. 点A、C的坐标分别是(-1,0)、(0, ).
(1)? 求此抛物线对应的函数解析式;
(2)? 若点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值.练习 2、已知抛物线
与x轴有两个交点.
(1)求k的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A在点B的左侧,点D是抛物线的顶点.如果⊿ABD是等腰直角三角形,求抛物线的解析式;
(3)在(2)的条件下.抛物线与y轴交于点C, 点E在y轴的正半轴上且以A、O、E为顶点的三角形与⊿AOC相似。求点E坐标.
谢谢大家
点(- 2,0),在y轴上的截距
为- 3,对称轴 x=2,求它的
解析式.练习2.抛物线y=x2-2(m-1)x+n过点(2,4),且其顶点在直线y=2x+1上,
(1)求这抛物线的解析式.
(2)求直线y=2x+1与抛物线的对称轴x轴所围成的三角形的面积.121或-15、已知如图A(1,1),AB=3,AB∥x轴OxyAB则点B的坐标为__________.(4,1)引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?1、求点A、B、C的坐标.2、求过点A、B、C的抛物线的函数解析式.3、你能算出丁的身高吗?引例:在跳大绳时,绳甩到最高处的形状可近似的看作抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,根据以上信息你能知道学生丁的身高吗?4、若现有一身高为1.625m的同学也想参加这个活动,请问他能参加这个活动吗?若能,则他应离甲多远的地方进入?若不能,请说明理由?若身高为1.7m呢?2、设:抛物线的函数解析式为:由题意可得:解得:∴抛物线的函数解析式为:∴该同学应该在离甲同学1.5m至2.5m处.例1.如图26.3.1,一位运动员推铅
球,铅球行进高度y(m)与水平距离x
(m)之间的关系是,问此运动员把铅球推出多远?解 如图,铅球落在x轴上,则y=0,
因此,解方程,得所以,此运动员把铅球推出了10米.(不合题意,舍去).例2.如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,点O是水池中心,OA=1.25米.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.(1)若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流最大高度应达多少米?(精确到0.1m).分析 这是一个运用抛物线的有关知识解决实际问题的应用题,首先必须将水流抛物线放在直角坐标系中,如图26.3.3,我们可以求出抛物线的函数关系式,再利用抛物线的性质即可解决问题. 确定二此函数的关系式的一般方法是待定系数法,在选择把二次函数的关系式设成什么形式时,可根据题目中的条件灵活选择,以简单为原则.二次函数的关系式可设如下二种形式:
(1)一般式:(2)顶点式:给出两点,且其中一点为顶点时可利用此式来求.给出三点坐标可利用此式来求.回顾与反思问题2 一个涵洞成抛物线形,它的截面如图.
现测得,当水面宽AB=1.6 m时,涵洞
顶点与水面的距离为2.4 m.这时,离
开水面1.5 m处,涵洞宽ED是多少?
是否会超过1 m?如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,
求(1)以这一部分抛物线
为图象的函数解析式,并写
出x的取值范围;
(2) 有一辆宽2.8米,高
1米的农用货车(货物最高
处与地面AB的距离)能否通
过此隧道?问题3画出 函数的图象,根据图象回答下列问题.
图象与x 轴交点的坐标是什么?
当x 取何值时,y=0?这里x的取值
与方程 有什么关系?(3)当x 取何值时,y<0?当x取何值时,y>0?
(4)能否用含有x的不等式来描述(3)
中的问题?1、抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点. 点A、C的坐标分别是(-1,0)、(0, ).
(1)? 求此抛物线对应的函数解析式;
(2)? 若点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值.练习 2、已知抛物线
与x轴有两个交点.
(1)求k的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A在点B的左侧,点D是抛物线的顶点.如果⊿ABD是等腰直角三角形,求抛物线的解析式;
(3)在(2)的条件下.抛物线与y轴交于点C, 点E在y轴的正半轴上且以A、O、E为顶点的三角形与⊿AOC相似。求点E坐标.
谢谢大家
