焦岱初中探索三角形的相识条件

探索三角形相识条件
一、填空
1．△ABC中，∠BAC=90，AD⊥BC于D，图中共有 对相似三角形．
2．Rt△ABC中，∠ACB=90，CD⊥AB于D，AD=4，BD=2，则CD =_______，AC =________．
3．△ABC中，DE∥BC交AB于D，AC于E，AB=12，AD-DB=4，BC=9，则DE=________．
4．△ABC中AB=AC=10，∠A=36°，BD是角平分线交AC于D，则DC________．
5．△ABC中P是AB上一点，且∠ACP=∠B，AC=4，AB=6，则PB=________．
6．如图，矩形ABCD中，AB=2，BC=3，E是AD的中点，则点C到BE的距离CF= ．
二、选择
7．下列图形中不一定相似的是( )
A．各有一个角等于45°的两个等腰三角形
B．各有一个角等于60°的两个等腰三角形
C．两个等腰直角三角形
D．各有一个角等于105°的两个等腰三角形
8．△ABC中，D，E分别是AB，AC上一点，若∠AED=∠B，则下列各式中，成立的是( )
A．AD∶AB=AE∶AC B．AD∶BD=AE∶CE C．AD·AB=AE·AC D．AD·BD=AE·CE
9．在Rt△ABC中，∠C=90°，CD⊥AB于D，且BC∶AC=2∶3，则BD∶AD = ( )
A．2:3 B．4:9 C．2:5 D．
10．在△ABC中，AD⊥BC于D，DE⊥AB于E，DF⊥AC于F，则下列式子中错误的是( )
A．AD= BD·DC B．CD= CF·CA C．DE= AE·EB D．AD= AF·AC
11．梯形ABCD中，AD∥BC，∠A=90°，AC⊥BD，AD=1，BC=4，则两条对角线AC∶BD为( )
A．4∶1 B．2∶1 C． D． 2:
12．如图，在等边△ABC中，P是BC上一点，D为AC上一点，且∠APD=60°，BP = 1，CD =，则△ABC的边长为( )
A． 3 B． 4 C． 5 D． 6
13．如图， 等边△ABC，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F．
⑴试说明△ABD≌△BCE．；
⑵△AEF与△ABE相似吗 说说你的理由；
⑶BD2=AD·DF吗 请说明理由．
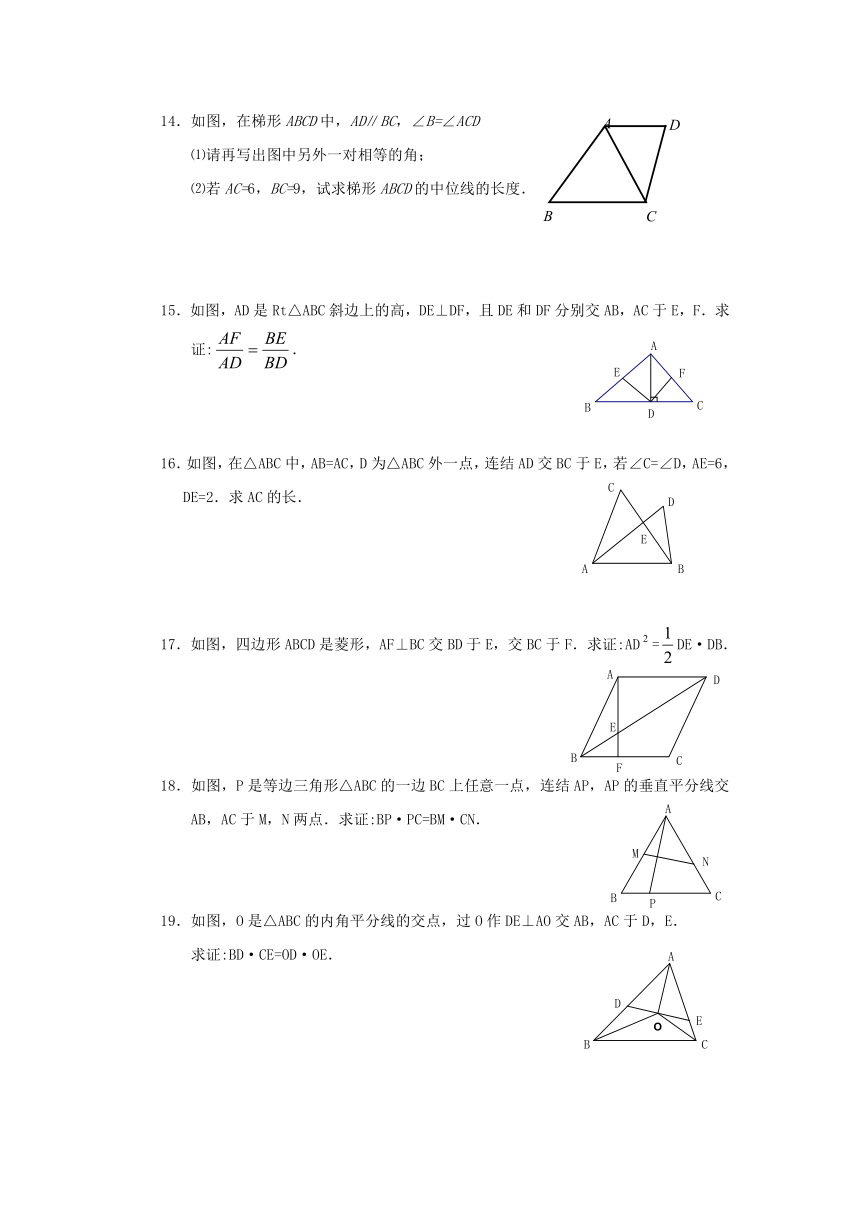
14．如图，在梯形ABCD中，AD∥BC，∠B=∠ACD
⑴请再写出图中另外一对相等的角；
⑵若AC=6，BC=9，试求梯形ABCD的中位线的长度．
15．如图，AD是Rt△ABC斜边上的高，DE⊥DF，且DE和DF分别交AB，AC于E，F．求证:．
16．如图，在△ABC中，AB=AC，D为△ABC外一点，连结AD交BC于E，若∠C=∠D，AE=6，DE=2．求AC的长．
17．如图，四边形ABCD是菱形，AF⊥BC交BD于E，交BC于F．求证:AD=DE·DB．
18．如图，P是等边三角形△ABC的一边BC上任意一点，连结AP，AP的垂直平分线交AB，AC于M，N两点．求证:BP·PC=BM·CN．
19．如图，O是△ABC的内角平分线的交点，过O作DE⊥AO交AB，AC于D，E．
求证:BD·CE=OD·OE．
20．已知:如图，△ABC中，AD是∠BAC的平分线，AD的垂直平分线交AD于E，交BC的延长线于F．求证：⑴FD= FB·FC；⑵AB:AC=BF:CF．
21．如图，在等腰梯形ABCD中，AD∥B ( http: / / www.21cnjy.com )C，AD=3㎝，BC=7㎝，∠B=60°，P为下底BC上一点（不与B、C重合），连结AP，过P点作PE交DC于E，使得∠APE=∠B．⑴求证：△ABP∽△PCE；⑵求等腰梯形的腰AB的长；⑶在底边BC上是否存在一点P，使得DE∶EC=5∶3 如果存在，求出BP的长，如果不存在，请说明理由．
22．如图，已知△ABC中，∠ACB=90，AC=BC，点E，F在AB上，∠ECF=45°．
⑴求证:△ACF∽△BEC；⑵设△ABC的面积为S，求证: AF·BE=2S．
23．已知，梯形ABCD中，AD∥BC，AD24．如图，在△ABC中，∠BAC=90° ( http: / / www.21cnjy.com )D为BC的中点，AE⊥AD，AE交CB的延长线于点E．⑴求证:△EAB∽△ECA；⑵△ABE和△ADC是否一定相似 如果相似，加以说明，如果不相似，那么增加一个怎样的条件， △ABE和△ADC一定相似．
4．6探索三角形相似的条件⑵
1．三；2．2，2；3．6；4；15－5；5．；6．2.4；7．A；8．C；9．B；10．A；11．B；12．A；13．⑴略．⑵相似，由⑴得∠AFE=∠BAC=60，∠AEF公共．⑶由△BDF∽△ABD得: ，即BD=AD·DF．
14．⑴∠BAC=∠D或∠CAD=∠ACB．⑵由△ABC∽△ACD得，解得:AD= 4，所以中位线的长= 6.5．
15．证: △ADF∽△BDE即可．
16．AC = 4．
17．提示:连结AC交BD于O．
18．连结PM，PN．证: △BPM∽△CPN即可．
19．证△BOD∽△EOC即可．
20．⑴连结AF．证; △ACF∽△BAF可得AF=FB·FC，即FD=FB·FC．⑵由⑴相似可得:
，，即．
21．⑴略．⑵作AF//CD交BC与F．可求得AB=4．⑶存在．设BP=，由⑴可得，解得=1， = 6．所以BP的长为1cm或6cm．
22．⑴由∠AFC=∠BCE=∠BCF+45，∠A=∠B=45可证得相似．⑵由⑴得AF·BE=AC·BC
=2S．
23． ⑴略． ⑵△ABP∽△DPQ， ，，得=－+－2．(1＜＜4)．
24． ⑴略． ⑵不相似．增加的条件为: ∠C=30或∠ABC=60．
D
A
B
C
60°
A
E
P
D
C
B
45°
A
E
F
B
C
B
C
D
A
P
E
Q
B
C
D
A
P
A
B
D
E
C