相似三角形的判定(预备定理)[下学期]
文档属性
| 名称 | 相似三角形的判定(预备定理)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 908.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-29 11:45:00 | ||
图片预览


文档简介
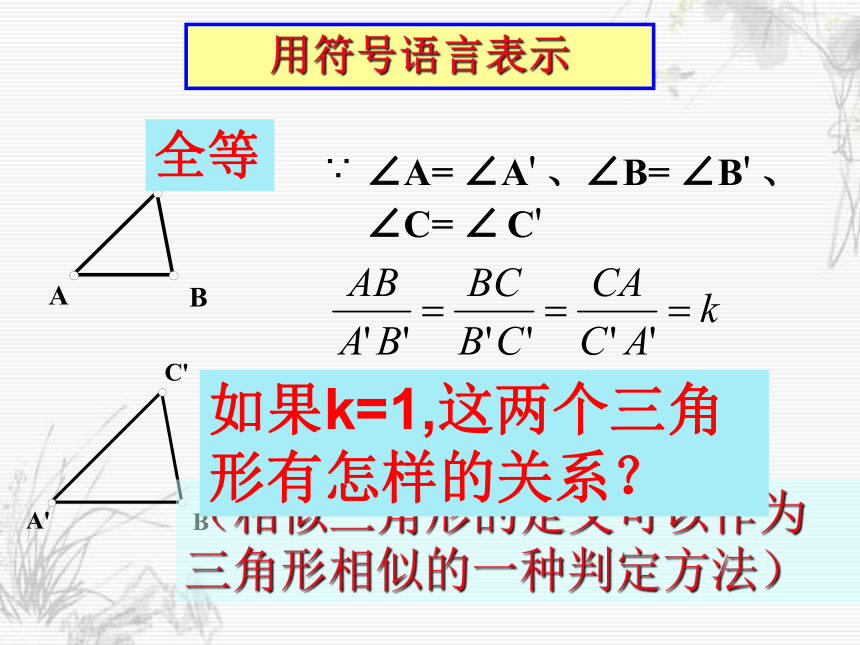
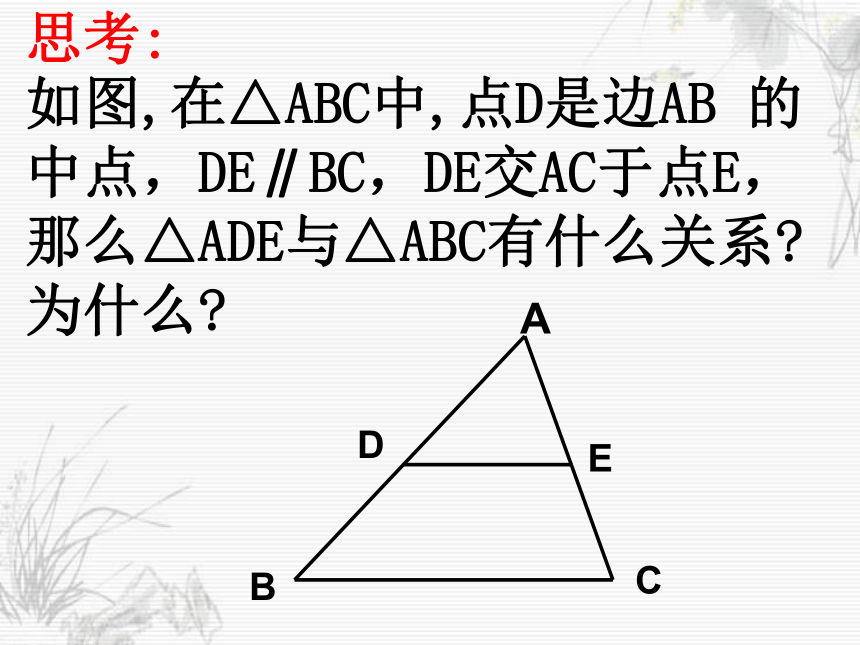
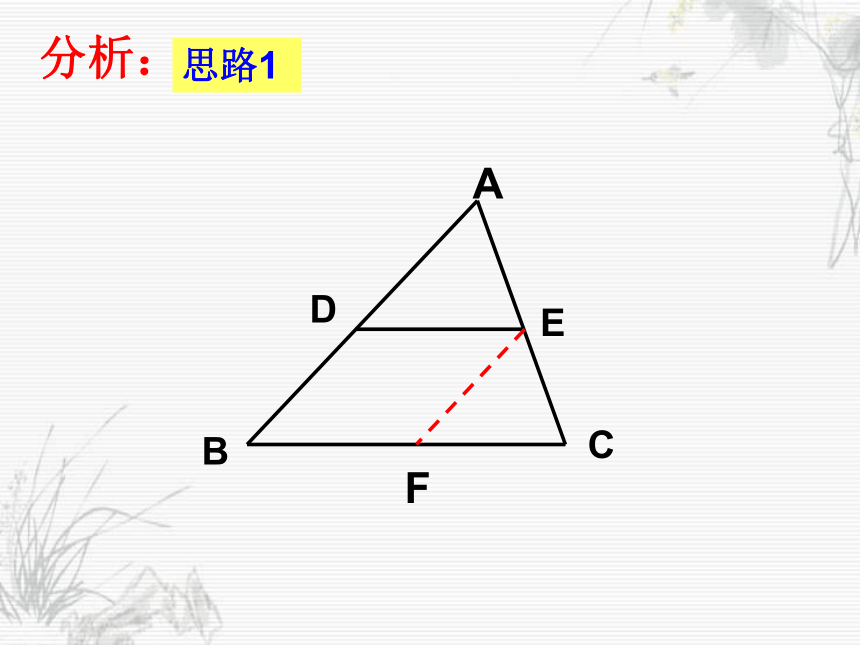
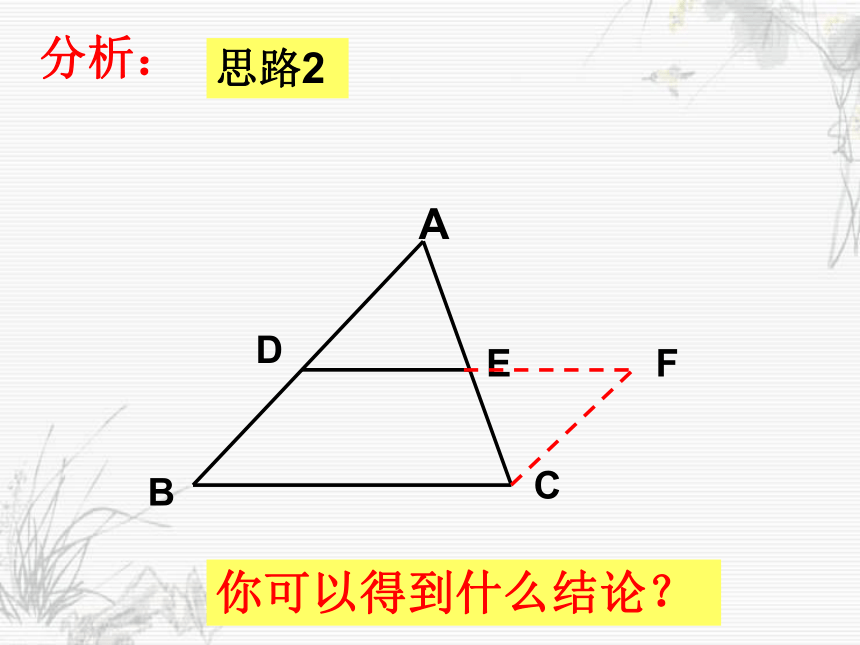
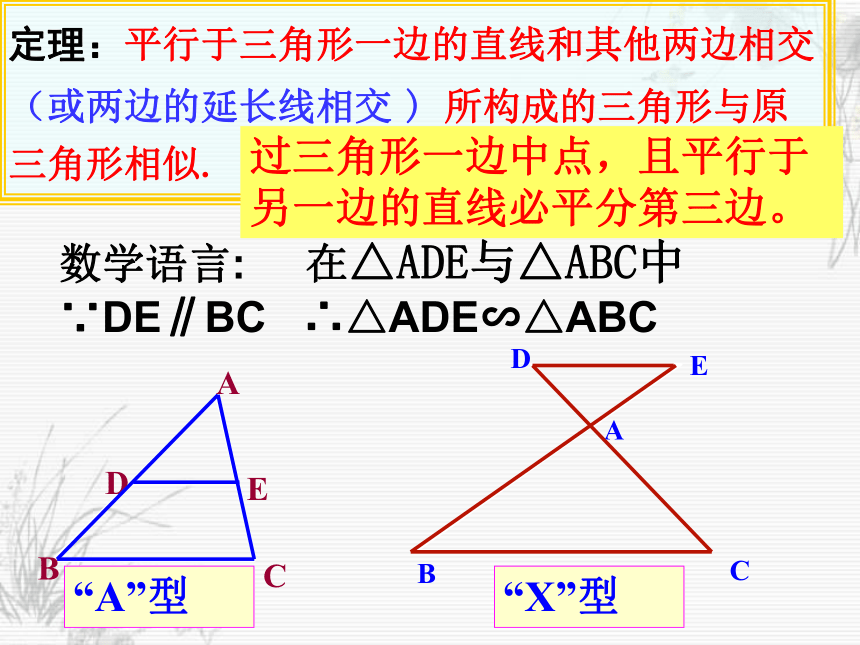
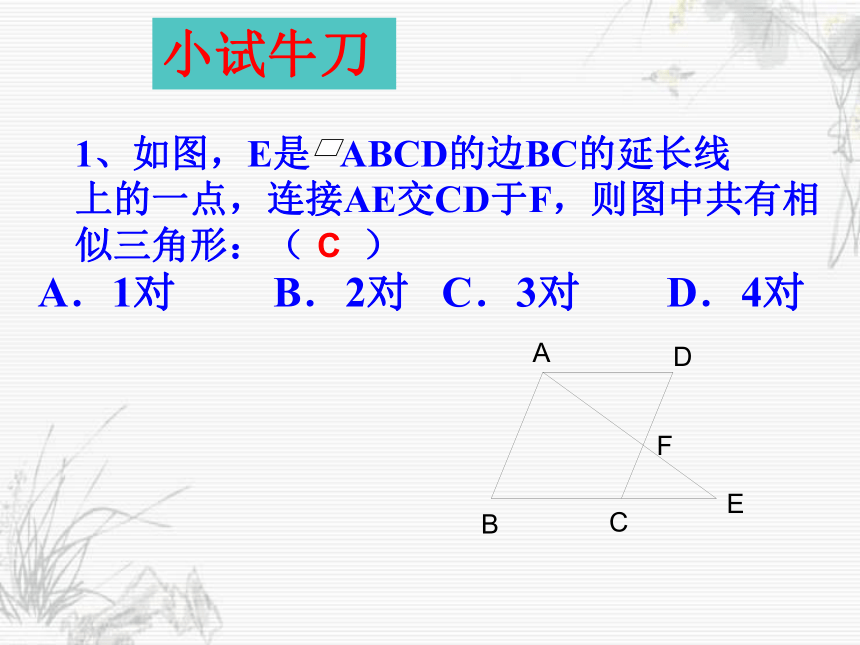
课件20张PPT。27.2.1 相似三角形的判定(预备定理) 相似三角形定义:我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。想一想:什么叫相似三角形?如何判定三角形相似?用符号语言表示∴ △ABC∽△A'B'C'(相似三角形的定义可以作为三角形相似的一种判定方法)如果k=1,这两个三角形有怎样的关系?全等思考:如图,在△ABC中,点D是边AB 的中点,DE∥BC,DE交AC于点E,那么△ADE与△ABC有什么关系?为什么?分析:F思路1分析:F思路2你可以得到什么结论?定理:平行于三角形一边的直线和其他两边相交 (或两边的延长线相交 ) 所构成的三角形与原三角形相似.数学语言: 在△ADE与△ABC中∵DE∥BC ∴△ADE∽△ABC“A”型 “X”型 过三角形一边中点,且平行于另一边的直线必平分第三边。1、如图,E是 ABCD的边BC的延长线
上的一点,连接AE交CD于F,则图中共有相
似三角形:( )
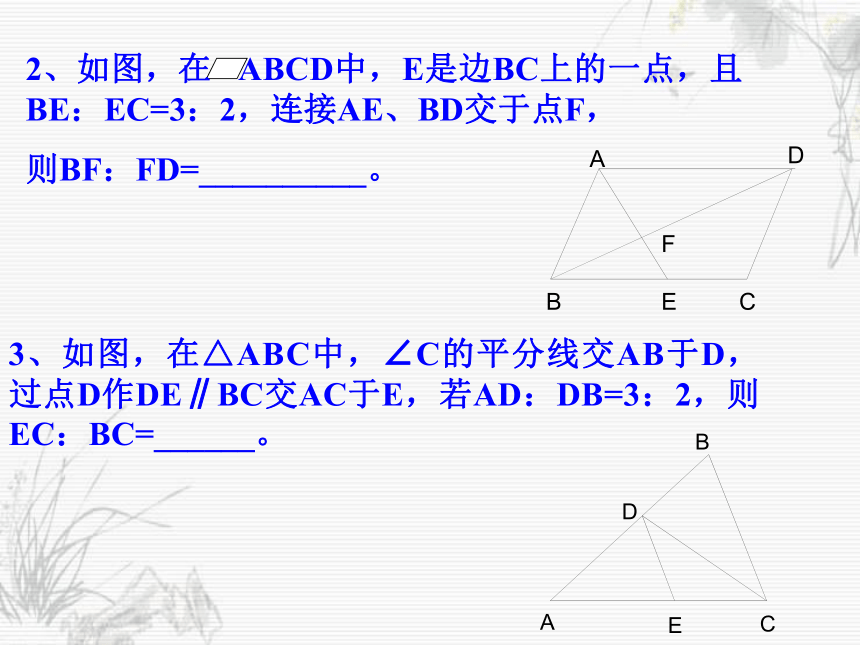
A.1对 B.2对 C.3对 D.4对C小试牛刀2、如图,在 ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,
则BF:FD=__________。3、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。例1.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)∵ DE ∥ BC△ADE∽△ABC∠AED=∠C=400.∵ △ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.例2 如图所示,已知AB∥EF ∥ CD,若AB=6厘米,CD=9厘米,求EF的长。ABECDF例3 如图,矩形ABCD中,AB=8,BC=6,对角线AC 上有一个动点P(不包括点A 和点C)。设AP=X,四边形PBCD的面积为y.(1)写出关于的函数关系,并确定自变量的取值范围.(2)有人提出一个判断:”关于动点P, △PBC的面积与△PAD面积之和为常数.”请你说明此判断是否正确,并说明理由.分析:E1.如图在△ABC中,DG∥EH∥FI∥BC
(1)请找出图中所有的相似三角形;
△ADG∽△AEH∽△AFI∽△ABC运用(2)如果AG:GH:HI :IC =1:2:3 :4
那么DG:EH:FI :BC =___________。 2.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE观察1.如图, 已知DE∥BC,EF∥AB,请尽可能多地找出图中的相似三角形,并说明理由。△ADE∽△ABC∽△EFC 2.已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC观察挑战已知:如图,在△ ABC中, ∠ ACB的平分线CD交AB于点D. 求证:小结通过这节课学习有那些收获!不经历风雨,怎么见彩虹没有人能随随便便成功!再见
上的一点,连接AE交CD于F,则图中共有相
似三角形:( )
A.1对 B.2对 C.3对 D.4对C小试牛刀2、如图,在 ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,
则BF:FD=__________。3、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。例1.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)∵ DE ∥ BC△ADE∽△ABC∠AED=∠C=400.∵ △ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.例2 如图所示,已知AB∥EF ∥ CD,若AB=6厘米,CD=9厘米,求EF的长。ABECDF例3 如图,矩形ABCD中,AB=8,BC=6,对角线AC 上有一个动点P(不包括点A 和点C)。设AP=X,四边形PBCD的面积为y.(1)写出关于的函数关系,并确定自变量的取值范围.(2)有人提出一个判断:”关于动点P, △PBC的面积与△PAD面积之和为常数.”请你说明此判断是否正确,并说明理由.分析:E1.如图在△ABC中,DG∥EH∥FI∥BC
(1)请找出图中所有的相似三角形;
△ADG∽△AEH∽△AFI∽△ABC运用(2)如果AG:GH:HI :IC =1:2:3 :4
那么DG:EH:FI :BC =___________。 2.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE观察1.如图, 已知DE∥BC,EF∥AB,请尽可能多地找出图中的相似三角形,并说明理由。△ADE∽△ABC∽△EFC 2.已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC观察挑战已知:如图,在△ ABC中, ∠ ACB的平分线CD交AB于点D. 求证:小结通过这节课学习有那些收获!不经历风雨,怎么见彩虹没有人能随随便便成功!再见
