天津市部分区2022-2023学年高二下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 天津市部分区2022-2023学年高二下学期期末考试数学试题(Word版含答案) | 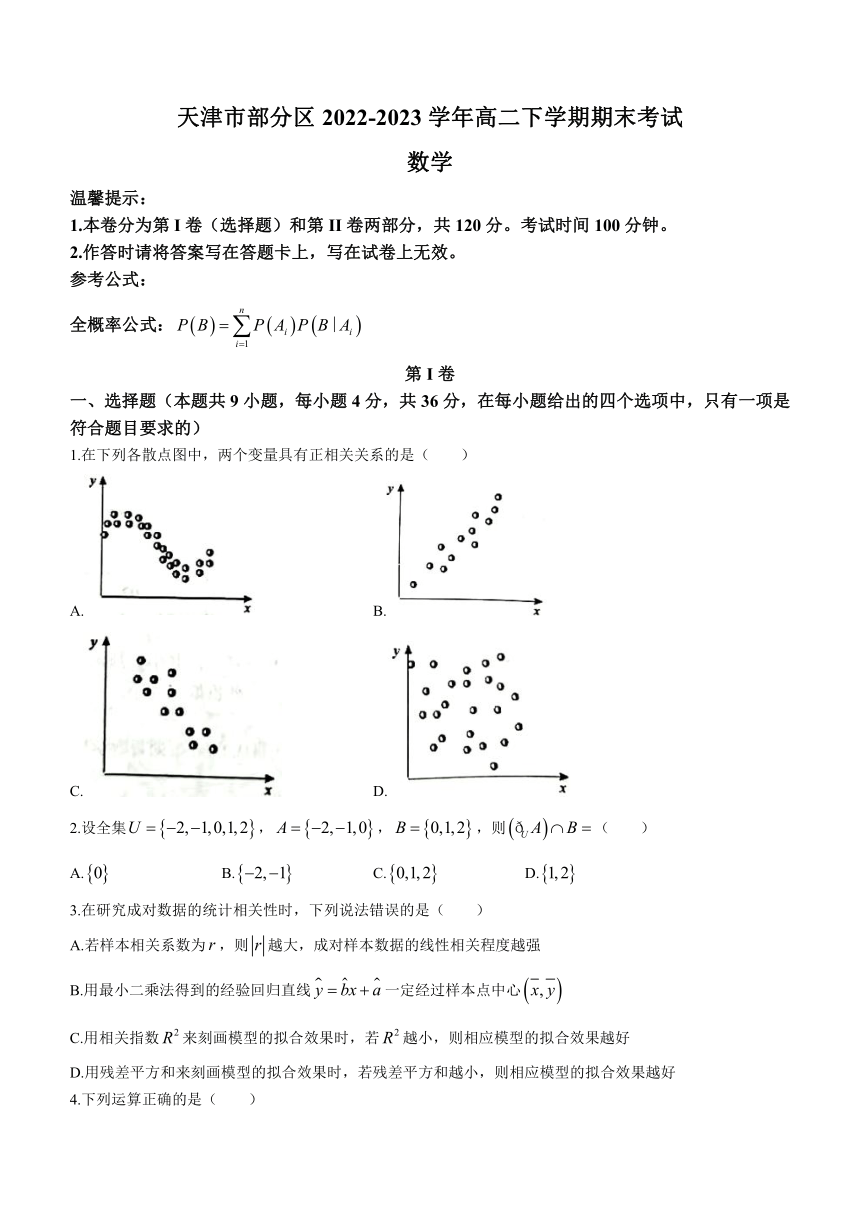 | |
| 格式 | docx | ||
| 文件大小 | 380.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 09:03:11 | ||
图片预览




文档简介
天津市部分区2022-2023学年高二下学期期末考试
数学
温馨提示:
1.本卷分为第I卷(选择题)和第II卷两部分,共120分。考试时间100分钟。
2.作答时请将答案写在答题卡上,写在试卷上无效。
参考公式:
全概率公式:
第I卷
一、选择题(本题共9小题,每小题4分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列各散点图中,两个变量具有正相关关系的是( )
A. B.
C. D.
2.设全集,,,则( )
A. B. C. D.
3.在研究成对数据的统计相关性时,下列说法错误的是( )
A.若样本相关系数为,则越大,成对样本数据的线性相关程度越强
B.用最小二乘法得到的经验回归直线一定经过样本点中心
C.用相关指数来刻画模型的拟合效果时,若越小,则相应模型的拟合效果越好
D.用残差平方和来刻画模型的拟合效果时,若残差平方和越小,则相应模型的拟合效果越好
4.下列运算正确的是( )
A. B.
C. D.
5.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.某地区空气质量监测资料表明,一天的空气质量为优的概率是0.8,连续两天的空气质量为优的概率是0.6.已知某天的空气质量为优,则随后一天的空气质量为优的概率是( )
A.0.75 B.0.7 C.0.6 D.0.45
7.从1,2,3,4,5五个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位数,这样的三位数共有( )
A.24个 B.36个 C.48个 D.54个
8.已知每门大炮每次击中目标的概率都是0.5,现有10门大炮同时对某一目标各射击一次.记事件“恰好击中目标3次”的概率为,若击中目标一次记2分,记10门大炮总得分的期望为,则,的值分别为( )
A.,5 B.,10 C.,5 D.,10
9.已知函数,,.若恰有2个零点,则实数的取值范围是( )
A. B. C. D.
第II卷
二、填空题(本大题共6小题,每小题4分,双空题每个空2分,满分24分)
10.曲线在点处的切线方程为______.
11.在的展开式中,常数项为______.
12.已知随机变量,若,则______.
13.某单位有,两个食堂,小李周一随机选择一个食堂用餐.如果周一去食堂,那么周二去食堂的概率为0.4;如果周一去食堂,那么周二去食堂的概率为0.6.小李周二去食堂的概率为______.
14.已知,若,,则______,______.
15.已知函数,则______;若,不等式恒成立,则实数的取值范围是______.
三、解答题(本大题共60分,解答应写出文字说明、演算步骤或推证过程)
16.(本小题满分11分)
已知函数(,且)的图象经过点.
(I)求的值;
(II)求在区间上的最大值;
(III)若函数,求证:在区间内存在零点.
17.(本小题满分12分)
网购是当前社会重要的购物方式,某电商对其旗下的一家专营店近五年来每年的利润额(单位:万元)与时间第年进行了统计,得到如下数据:
1 2 3 4 5
2.6 3.1 4.5 6.8 8.0
(I)当相关系数满足时,线性相关程度很高,可用线性回归模型拟合.依据表中给出的数据,判断是否可用线性回归模型拟合与的关系,并加以说明;
(II)试用最小二乘法求出与的回归方程,并预测当时的利润额.
附:,
,
参考数据:,,,.
18.(本小题满分12分)
为加强素质教育,提升学生综合素养,某中学为学生提供了“科技”和“艺术”两门选修课.为了了解选择“科技”或“艺术”是否与性别有关,现随机抽取了100人.
(I)补全下面列联表;
性别 科技 艺术 共计
男生 40 50
女生
共计 30
(II)是否有的把握认为选择“科技”或“艺术”与性别有关?
参考公式:,其中.
参考附表:
0.100 0.050 0.025
2.706 3.841 5.024
19.(本小题满分12分)
端午节吃粽子是我国的传统习俗,一盘中有8个粽子,其中豆沙粽2个,蜜枣粽6个,这两种粽子的外观完全相同,从中随机取出3个.
(I)求既有豆沙粽又有蜜枣粽的概率;
(II)设表示取到豆沙粽的个数,求随机变量的分布列与数学期望.
20.(本小题满分13分)
已知函数.
(I)求曲线在点处的切线方程;
(II)设为的导函数,讨论在区间上的单调性;
(III)证明:对任意的,有.
高二数学参考答案
一、选择题:本大题共9小题,每小题4分,共36分.
题号 1 2 3 4 5 6 7 8 9
答案 B D C D A A B B C
二、填空题:本大题共6小题,每小题4分,双空题每个空2分,共24分.
10. 11. 12. 13.0.5
14.4;2 15.3;
三、解答题:本大题共5小题,共60分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分11分)
(1)因为函数,且的图象经过点,
所以. ………………………………………………2分
所以.………………………………………………………3分
(2)因为,所以.
所以在区间上单调递减. …………………………4分
所以在区间上的最大值是.……………………5分
所以. …………………………………………………6分
所以在区间上的最大值是.……………………………………7分
(3)因为,
所以. ………………………………………………8分
因为,,………………………………9分
所以,又在区间上的图象是一条连续的曲线,由
零点存在性定理可得:在区间内存在零点.……………11分
17.(本小题满分12分)
(1)可用,由题表,,
……2分
因为,,,
所以.………4分
故y与t的线性相关程度很高,可以用线性回归模型拟合.……5分
(2),…………………………………………7分
,…………………………………………8分
所以.…………………………………………………10分
当时,.…………………………………11分
预测该专营店在时的利润为万元.…………………………12分
18.(本小题满分12分)
【详解】(1)根据题意,补全列联表如下,
选科技 选艺术 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
…………………………………………每个空1分,共6分
(2)根据列联表数据,得
,
……10分
所以有的把握认为选择“科技”或“艺术”与性别有关.……12分
19.(本小题满分12分)
(1)依题意,既有豆沙粽又有蜜枣粽的概率为.……4分
(2)的可能取值为,…………………………5分
则,…………………………6分
,………………………………7分
,………………………………8分
所以的分布列如下:
……………………………………………………………………10分
所以.…………………………12分
20.(本小题满分12分)
(1)解:,即切点坐标为,………………………………1分
又,……………………2分
∴切线斜率………………………………3分
∴切线方程为:……………………………………4分
(2)解:因为,
所以,…………………………5分
令,
则, …………………………6分
∴在上单调递增,
∴…………………………………………7分
∴在上恒成立,
∴在上单调递增……………………………………8分
(3)解:原不等式等价于,
令,,
即证,………………………………………………9分
∵,
,……11分
由(2)知在上单调递增,
∴,
∴
∴在上单调递增,又因为,……………………12分
∴,所以命题得证………………………………………13分
数学
温馨提示:
1.本卷分为第I卷(选择题)和第II卷两部分,共120分。考试时间100分钟。
2.作答时请将答案写在答题卡上,写在试卷上无效。
参考公式:
全概率公式:
第I卷
一、选择题(本题共9小题,每小题4分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列各散点图中,两个变量具有正相关关系的是( )
A. B.
C. D.
2.设全集,,,则( )
A. B. C. D.
3.在研究成对数据的统计相关性时,下列说法错误的是( )
A.若样本相关系数为,则越大,成对样本数据的线性相关程度越强
B.用最小二乘法得到的经验回归直线一定经过样本点中心
C.用相关指数来刻画模型的拟合效果时,若越小,则相应模型的拟合效果越好
D.用残差平方和来刻画模型的拟合效果时,若残差平方和越小,则相应模型的拟合效果越好
4.下列运算正确的是( )
A. B.
C. D.
5.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.某地区空气质量监测资料表明,一天的空气质量为优的概率是0.8,连续两天的空气质量为优的概率是0.6.已知某天的空气质量为优,则随后一天的空气质量为优的概率是( )
A.0.75 B.0.7 C.0.6 D.0.45
7.从1,2,3,4,5五个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位数,这样的三位数共有( )
A.24个 B.36个 C.48个 D.54个
8.已知每门大炮每次击中目标的概率都是0.5,现有10门大炮同时对某一目标各射击一次.记事件“恰好击中目标3次”的概率为,若击中目标一次记2分,记10门大炮总得分的期望为,则,的值分别为( )
A.,5 B.,10 C.,5 D.,10
9.已知函数,,.若恰有2个零点,则实数的取值范围是( )
A. B. C. D.
第II卷
二、填空题(本大题共6小题,每小题4分,双空题每个空2分,满分24分)
10.曲线在点处的切线方程为______.
11.在的展开式中,常数项为______.
12.已知随机变量,若,则______.
13.某单位有,两个食堂,小李周一随机选择一个食堂用餐.如果周一去食堂,那么周二去食堂的概率为0.4;如果周一去食堂,那么周二去食堂的概率为0.6.小李周二去食堂的概率为______.
14.已知,若,,则______,______.
15.已知函数,则______;若,不等式恒成立,则实数的取值范围是______.
三、解答题(本大题共60分,解答应写出文字说明、演算步骤或推证过程)
16.(本小题满分11分)
已知函数(,且)的图象经过点.
(I)求的值;
(II)求在区间上的最大值;
(III)若函数,求证:在区间内存在零点.
17.(本小题满分12分)
网购是当前社会重要的购物方式,某电商对其旗下的一家专营店近五年来每年的利润额(单位:万元)与时间第年进行了统计,得到如下数据:
1 2 3 4 5
2.6 3.1 4.5 6.8 8.0
(I)当相关系数满足时,线性相关程度很高,可用线性回归模型拟合.依据表中给出的数据,判断是否可用线性回归模型拟合与的关系,并加以说明;
(II)试用最小二乘法求出与的回归方程,并预测当时的利润额.
附:,
,
参考数据:,,,.
18.(本小题满分12分)
为加强素质教育,提升学生综合素养,某中学为学生提供了“科技”和“艺术”两门选修课.为了了解选择“科技”或“艺术”是否与性别有关,现随机抽取了100人.
(I)补全下面列联表;
性别 科技 艺术 共计
男生 40 50
女生
共计 30
(II)是否有的把握认为选择“科技”或“艺术”与性别有关?
参考公式:,其中.
参考附表:
0.100 0.050 0.025
2.706 3.841 5.024
19.(本小题满分12分)
端午节吃粽子是我国的传统习俗,一盘中有8个粽子,其中豆沙粽2个,蜜枣粽6个,这两种粽子的外观完全相同,从中随机取出3个.
(I)求既有豆沙粽又有蜜枣粽的概率;
(II)设表示取到豆沙粽的个数,求随机变量的分布列与数学期望.
20.(本小题满分13分)
已知函数.
(I)求曲线在点处的切线方程;
(II)设为的导函数,讨论在区间上的单调性;
(III)证明:对任意的,有.
高二数学参考答案
一、选择题:本大题共9小题,每小题4分,共36分.
题号 1 2 3 4 5 6 7 8 9
答案 B D C D A A B B C
二、填空题:本大题共6小题,每小题4分,双空题每个空2分,共24分.
10. 11. 12. 13.0.5
14.4;2 15.3;
三、解答题:本大题共5小题,共60分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分11分)
(1)因为函数,且的图象经过点,
所以. ………………………………………………2分
所以.………………………………………………………3分
(2)因为,所以.
所以在区间上单调递减. …………………………4分
所以在区间上的最大值是.……………………5分
所以. …………………………………………………6分
所以在区间上的最大值是.……………………………………7分
(3)因为,
所以. ………………………………………………8分
因为,,………………………………9分
所以,又在区间上的图象是一条连续的曲线,由
零点存在性定理可得:在区间内存在零点.……………11分
17.(本小题满分12分)
(1)可用,由题表,,
……2分
因为,,,
所以.………4分
故y与t的线性相关程度很高,可以用线性回归模型拟合.……5分
(2),…………………………………………7分
,…………………………………………8分
所以.…………………………………………………10分
当时,.…………………………………11分
预测该专营店在时的利润为万元.…………………………12分
18.(本小题满分12分)
【详解】(1)根据题意,补全列联表如下,
选科技 选艺术 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
…………………………………………每个空1分,共6分
(2)根据列联表数据,得
,
……10分
所以有的把握认为选择“科技”或“艺术”与性别有关.……12分
19.(本小题满分12分)
(1)依题意,既有豆沙粽又有蜜枣粽的概率为.……4分
(2)的可能取值为,…………………………5分
则,…………………………6分
,………………………………7分
,………………………………8分
所以的分布列如下:
……………………………………………………………………10分
所以.…………………………12分
20.(本小题满分12分)
(1)解:,即切点坐标为,………………………………1分
又,……………………2分
∴切线斜率………………………………3分
∴切线方程为:……………………………………4分
(2)解:因为,
所以,…………………………5分
令,
则, …………………………6分
∴在上单调递增,
∴…………………………………………7分
∴在上恒成立,
∴在上单调递增……………………………………8分
(3)解:原不等式等价于,
令,,
即证,………………………………………………9分
∵,
,……11分
由(2)知在上单调递增,
∴,
∴
∴在上单调递增,又因为,……………………12分
∴,所以命题得证………………………………………13分
同课章节目录
