2023-2024学年冀教版八年级上学期数学十六章 轴对称与中心对称 复习课课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年冀教版八年级上学期数学十六章 轴对称与中心对称 复习课课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 695.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第十六章回顾与反思
冀教版
八年级上册
1.如图,下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是________.(填序号)
知识应用
知识点一 轴对称与轴对称图形
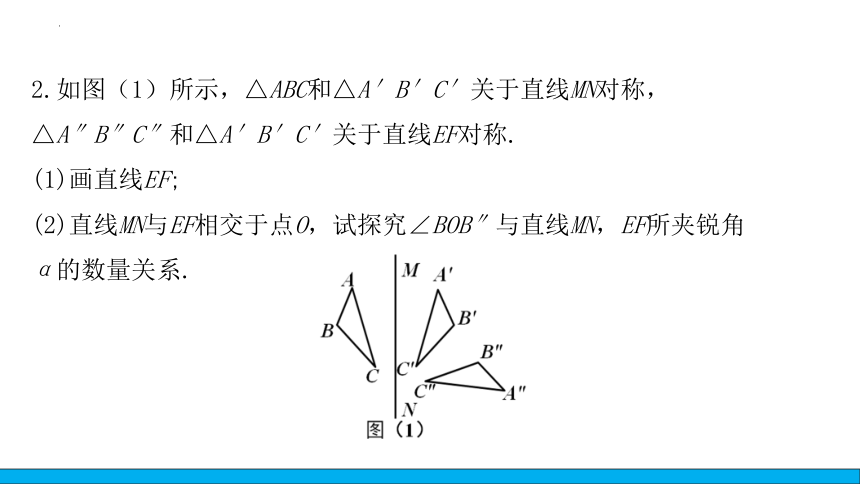
2.如图(1)所示,△ABC和△A′B′C′关于直线MN对称,△A″B″C″和△A′B′C′关于直线EF对称.
(1)画直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
知识点二 中心对称及中心对称图形
D
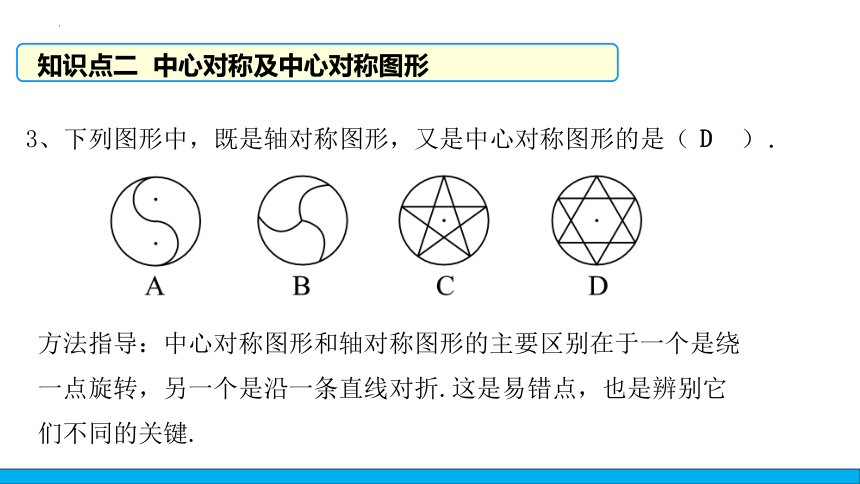
3、下列图形中,既是轴对称图形,又是中心对称图形的是( ).
方法指导:中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
4、如图,已知四边形ABCD与四边形EFGH关于直线BD上的某个点成中心对称,则点B的对称点是( )
A.点E B.点F
C.点G D.点H
D
5.如图,△ABC是 轴对称图形,且直线AD是△ABC的对称轴,点E,F是
线段AD上的任意两点,若△ABC的面积为12 cm2,则图中阴影部分的面
积是________cm2.
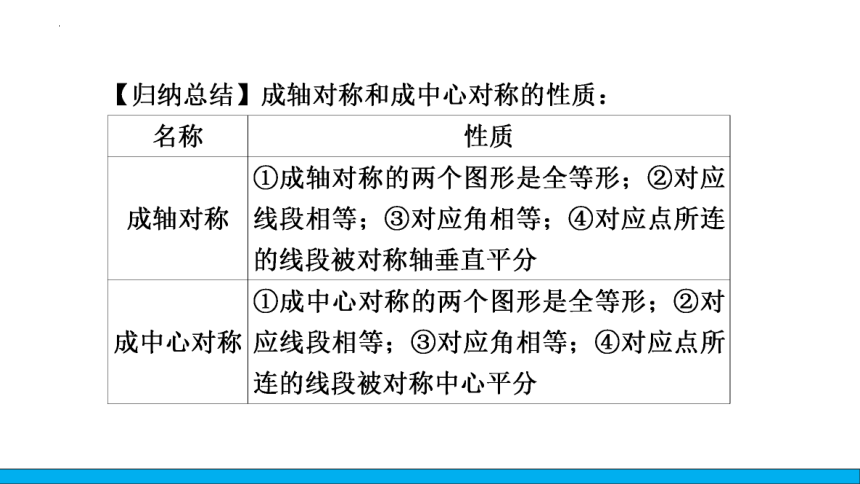
知识点三 轴对称与轴对称图形性质
应用4 线段垂直平分线、角平分线的性质和判定
6.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,
DF⊥AC,E,F为垂足,连接EF交AD于点G,试判断AD与EF
垂直吗?并说明理由.
7.如图,A,B两点在直线l的两侧,在l上找一点C,使点C到点A,B的距离之和最大,并说明理由.
知识点五 最短路径的应用
在现实生活中,经常会遇到寻找最短路径的问题,解决最短路径问题的基本原理是什么呢?
拓展 :∠AOB的内部有一点P,在射线OA,OB上各取一点P1,
P2,使得△PP1P2的周长最小,作出点P1,P2,叙述作图过程(作法),
保留作图痕迹.
总结提升
【归纳总结】利用轴对称解决最短路径问题的方法:
利用轴对称求最短路径问题应用的基本事实是“两
点之间线段最短”.通常先找到其中一点关于对称
轴的对称点,再连接这个对称点与另外一点,找到
与对称轴的交点即可.
三 本章操作题
如何利用尺规作线段的垂直平分线和角平分线呢?
利用尺规作线段垂直平分线和角平分线的依据分别是什么?
1、尺规作图
1、 如图,要在公路MN旁修建一个货物中转站P,分别向A,B
两个开发区运货.开发区A,B之间还有一条公路CD,货物中转
站P应建在哪里,才能使其到A,B的距离相等,且到两条公路的
距离也相等?(在图上找出点P,并保留作图痕迹)
【归纳总结】两个尺规作图的依据:
线段垂直平分线——三角形全等(SSS)
角平分线——三角形全等(SSS)
2、图案设计
图①是利用正方形各边中点和弧的中点设计的正方形瓷砖图
案,用四块如图①所示的正方形瓷砖拼成一个新的正方形,使拼
成的图案既是轴对称图形,又是中心对称图形.请你在图②和图
③中各画一种拼法(要求两种拼法各不相同).
【归纳总结】设计图案的两点说明:
作一个图形关于某条直线的轴对称图形,是逆用轴对称的性质来进
行的;作一个图形关于某点的中心对称图形,是逆用中心对称的性
质来进行的.
课堂小结
【作业设计】
基础性作业:课本复习题A组(必做)
拓展性作业:复习题 B 组、 C组(选作)
实践性作业: (必做)
实践与操作:如图,图①是以正方形两顶点为圆心,边长为半径,
画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案
经过图形变换拼成的一个中心对称图形.(1)请你依照图②,用段相等的圆弧(小于或等于半圆)在图③中重新设计一个不同的轴对称图形;(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
感谢聆听
第十六章回顾与反思
冀教版
八年级上册
1.如图,下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是________.(填序号)
知识应用
知识点一 轴对称与轴对称图形
2.如图(1)所示,△ABC和△A′B′C′关于直线MN对称,△A″B″C″和△A′B′C′关于直线EF对称.
(1)画直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
知识点二 中心对称及中心对称图形
D
3、下列图形中,既是轴对称图形,又是中心对称图形的是( ).
方法指导:中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
4、如图,已知四边形ABCD与四边形EFGH关于直线BD上的某个点成中心对称,则点B的对称点是( )
A.点E B.点F
C.点G D.点H
D
5.如图,△ABC是 轴对称图形,且直线AD是△ABC的对称轴,点E,F是
线段AD上的任意两点,若△ABC的面积为12 cm2,则图中阴影部分的面
积是________cm2.
知识点三 轴对称与轴对称图形性质
应用4 线段垂直平分线、角平分线的性质和判定
6.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,
DF⊥AC,E,F为垂足,连接EF交AD于点G,试判断AD与EF
垂直吗?并说明理由.
7.如图,A,B两点在直线l的两侧,在l上找一点C,使点C到点A,B的距离之和最大,并说明理由.
知识点五 最短路径的应用
在现实生活中,经常会遇到寻找最短路径的问题,解决最短路径问题的基本原理是什么呢?
拓展 :∠AOB的内部有一点P,在射线OA,OB上各取一点P1,
P2,使得△PP1P2的周长最小,作出点P1,P2,叙述作图过程(作法),
保留作图痕迹.
总结提升
【归纳总结】利用轴对称解决最短路径问题的方法:
利用轴对称求最短路径问题应用的基本事实是“两
点之间线段最短”.通常先找到其中一点关于对称
轴的对称点,再连接这个对称点与另外一点,找到
与对称轴的交点即可.
三 本章操作题
如何利用尺规作线段的垂直平分线和角平分线呢?
利用尺规作线段垂直平分线和角平分线的依据分别是什么?
1、尺规作图
1、 如图,要在公路MN旁修建一个货物中转站P,分别向A,B
两个开发区运货.开发区A,B之间还有一条公路CD,货物中转
站P应建在哪里,才能使其到A,B的距离相等,且到两条公路的
距离也相等?(在图上找出点P,并保留作图痕迹)
【归纳总结】两个尺规作图的依据:
线段垂直平分线——三角形全等(SSS)
角平分线——三角形全等(SSS)
2、图案设计
图①是利用正方形各边中点和弧的中点设计的正方形瓷砖图
案,用四块如图①所示的正方形瓷砖拼成一个新的正方形,使拼
成的图案既是轴对称图形,又是中心对称图形.请你在图②和图
③中各画一种拼法(要求两种拼法各不相同).
【归纳总结】设计图案的两点说明:
作一个图形关于某条直线的轴对称图形,是逆用轴对称的性质来进
行的;作一个图形关于某点的中心对称图形,是逆用中心对称的性
质来进行的.
课堂小结
【作业设计】
基础性作业:课本复习题A组(必做)
拓展性作业:复习题 B 组、 C组(选作)
实践性作业: (必做)
实践与操作:如图,图①是以正方形两顶点为圆心,边长为半径,
画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案
经过图形变换拼成的一个中心对称图形.(1)请你依照图②,用段相等的圆弧(小于或等于半圆)在图③中重新设计一个不同的轴对称图形;(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
感谢聆听
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
