12.2三角形全等的判定(1)同步习题精讲课件
文档属性
| 名称 | 12.2三角形全等的判定(1)同步习题精讲课件 |  | |
| 格式 | zip | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 12:27:56 | ||
图片预览



文档简介
课件18张PPT。12.2 三角形全等的判定第1课时 边边边12.2 三角形全等的判定三边分别 的两个三角形全等,简写成“ ”或“ ”.边边边SSS相等 用“SSS”判定两个三角形全等
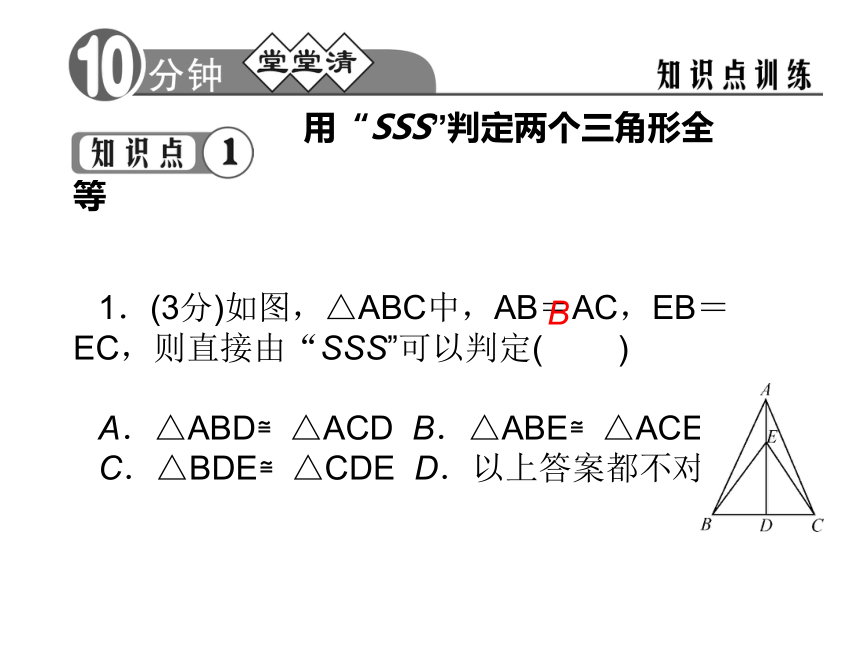
1.(3分)如图,△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
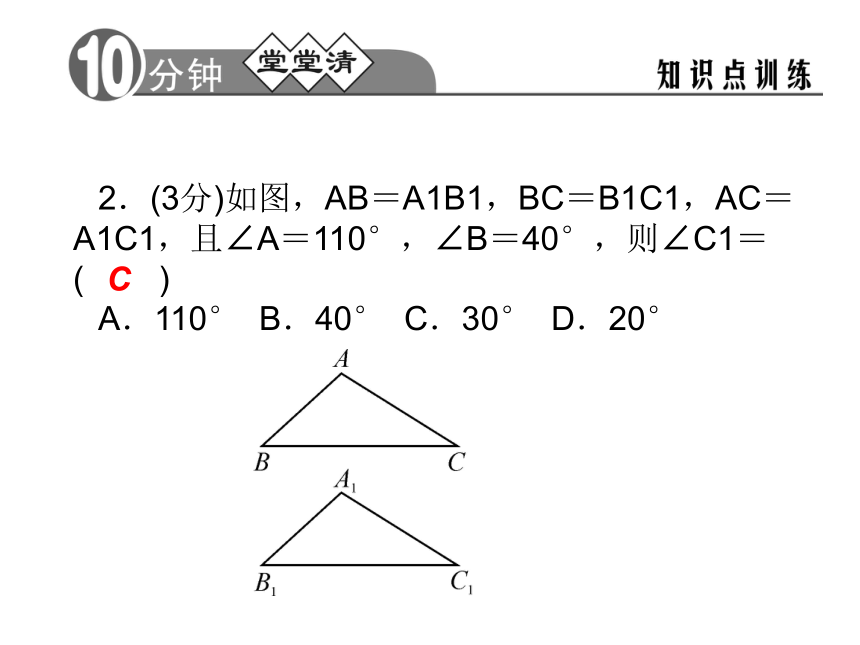
C.△BDE≌△CDE D.以上答案都不对B2.(3分)如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
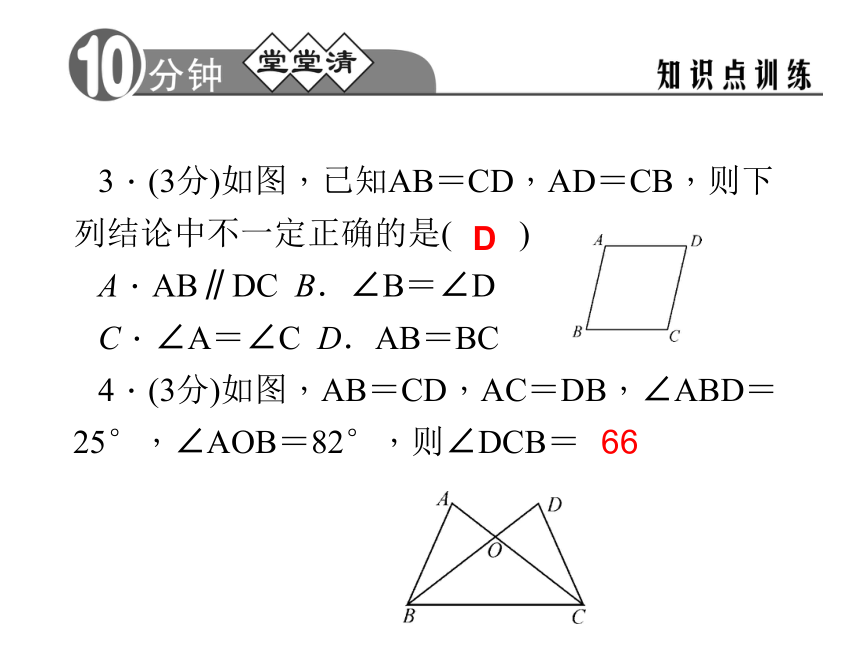
A.110° B.40° C.30° D.20°C3.(3分)如图,已知AB=CD,AD=CB,则下列结论中不一定正确的是( )
A.AB∥DC B.∠B=∠D
C.∠A=∠C D.AB=BC
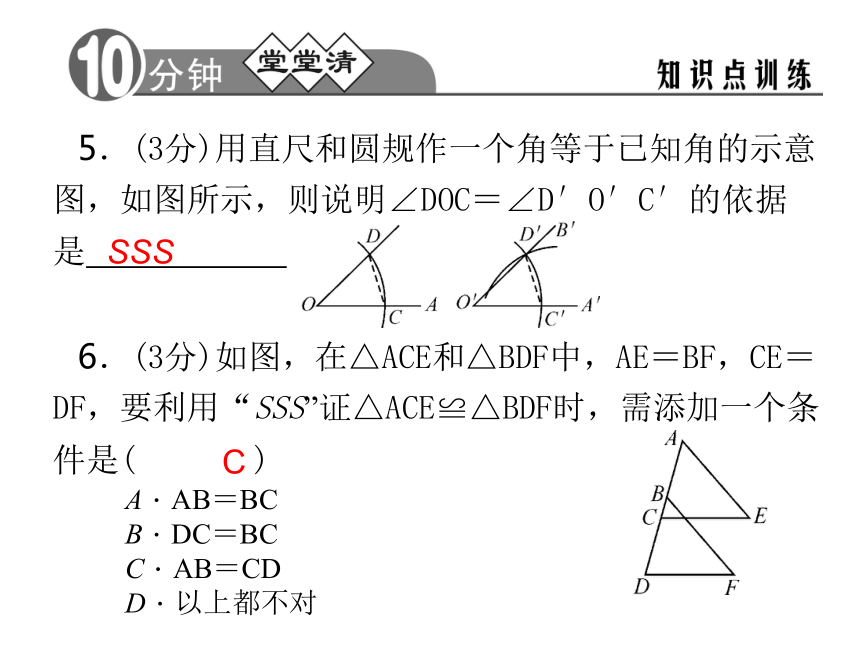
4.(3分)如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB= D665.(3分)用直尺和圆规作一个角等于已知角的示意图,如图所示,则说明∠DOC=∠D′O′C′的依据是 .
6.(3分)如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A.AB=BC
B.DC=BC
C.AB=CD
D.以上都不对SSSC7.(7分)如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.
解:证明:∵BD=CD,
∴BD+DE=CE+ED,即BE=CD.
∴在△ABE和△ACD中,
∴△ABE≌△ACD(SSS)8.(7分)如图,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.
解:连接BD.
∵在△CDB和△ADB中
∴△BDC≌△BDA(SSS),
∴∠A=∠C解:∠BAD=∠CAD,
理由:证△AEO≌△AFO(SSS)9.(8分)如图是雨伞的中截面,伞骨AB= AC,支撑杆OE=OF,AE= AB,AF= AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
一、选择题(每小题4分,共16分) 10.△ABC和△DEF中,AB=2,BC=3,CA=4,DE=4,EF=3,要使△ABC与△DEF全等,则DF等于( )
A.2 B.3
C.4 D.不能确定
A11.如图,AB=AC,BD=DC,则下列结论不正确的是( )
A.△ABD≌△ACD
B.∠ADB=90°
C.∠BAD=∠B
D.AD平分∠BAC
12.如图,OA=OB,OC=OD,AD=BC,则图中全等三角形的对数有( )
A.1对 B.2对 C.3对 D.4对
CC13.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③
C.③或① D.①或④A 二、填空题(每小题4分,共12分)
14.如图,AB=ED,AC=EC,C是BD边的中点,若∠A=36°,则∠E= . 36°15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 .
第15题图
16.如图,AB=DE,AF=DC,
EF=BC,∠AFB=70°,
∠CDE=80°,∠ABC= .第16题图AB=DC30°三、解答题(共32分)
17.(10分)如图,点E,F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O.
求证:AE∥CF.
解:∵BF=DE
∴BE=DF
在△ABE和△CDF中,
AB=CD,BE=DF,AE=CF,
∴△ABE≌△CDF
∴∠AEB=∠CFD
∴∠AEO=∠CFO
∴AE∥CF.18.(10分)如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
证明:∵AB=AC,
AD=AE,
BD=CE
∴△ABD≌△ACE,
∴∠2=∠ABD,∠1=∠BAD
∵∠3=∠ABD+∠BAD
∴∠3=∠1+∠2【综合运用】19.(12分)AC,BD相交于点O,且AB=DC,AC=DB,试判断∠A与∠D的大小关系.
解:连接BC.
在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠A=∠D.
1.(3分)如图,△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对B2.(3分)如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
A.110° B.40° C.30° D.20°C3.(3分)如图,已知AB=CD,AD=CB,则下列结论中不一定正确的是( )
A.AB∥DC B.∠B=∠D
C.∠A=∠C D.AB=BC
4.(3分)如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB= D665.(3分)用直尺和圆规作一个角等于已知角的示意图,如图所示,则说明∠DOC=∠D′O′C′的依据是 .
6.(3分)如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A.AB=BC
B.DC=BC
C.AB=CD
D.以上都不对SSSC7.(7分)如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.
解:证明:∵BD=CD,
∴BD+DE=CE+ED,即BE=CD.
∴在△ABE和△ACD中,
∴△ABE≌△ACD(SSS)8.(7分)如图,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.
解:连接BD.
∵在△CDB和△ADB中
∴△BDC≌△BDA(SSS),
∴∠A=∠C解:∠BAD=∠CAD,
理由:证△AEO≌△AFO(SSS)9.(8分)如图是雨伞的中截面,伞骨AB= AC,支撑杆OE=OF,AE= AB,AF= AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
一、选择题(每小题4分,共16分) 10.△ABC和△DEF中,AB=2,BC=3,CA=4,DE=4,EF=3,要使△ABC与△DEF全等,则DF等于( )
A.2 B.3
C.4 D.不能确定
A11.如图,AB=AC,BD=DC,则下列结论不正确的是( )
A.△ABD≌△ACD
B.∠ADB=90°
C.∠BAD=∠B
D.AD平分∠BAC
12.如图,OA=OB,OC=OD,AD=BC,则图中全等三角形的对数有( )
A.1对 B.2对 C.3对 D.4对
CC13.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③
C.③或① D.①或④A 二、填空题(每小题4分,共12分)
14.如图,AB=ED,AC=EC,C是BD边的中点,若∠A=36°,则∠E= . 36°15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 .
第15题图
16.如图,AB=DE,AF=DC,
EF=BC,∠AFB=70°,
∠CDE=80°,∠ABC= .第16题图AB=DC30°三、解答题(共32分)
17.(10分)如图,点E,F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O.
求证:AE∥CF.
解:∵BF=DE
∴BE=DF
在△ABE和△CDF中,
AB=CD,BE=DF,AE=CF,
∴△ABE≌△CDF
∴∠AEB=∠CFD
∴∠AEO=∠CFO
∴AE∥CF.18.(10分)如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
证明:∵AB=AC,
AD=AE,
BD=CE
∴△ABD≌△ACE,
∴∠2=∠ABD,∠1=∠BAD
∵∠3=∠ABD+∠BAD
∴∠3=∠1+∠2【综合运用】19.(12分)AC,BD相交于点O,且AB=DC,AC=DB,试判断∠A与∠D的大小关系.
解:连接BC.
在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠A=∠D.
