12.2三角形全等的判定(2)同步习题精讲课件
文档属性
| 名称 | 12.2三角形全等的判定(2)同步习题精讲课件 |  | |
| 格式 | zip | ||
| 文件大小 | 326.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 12:29:07 | ||
图片预览




文档简介
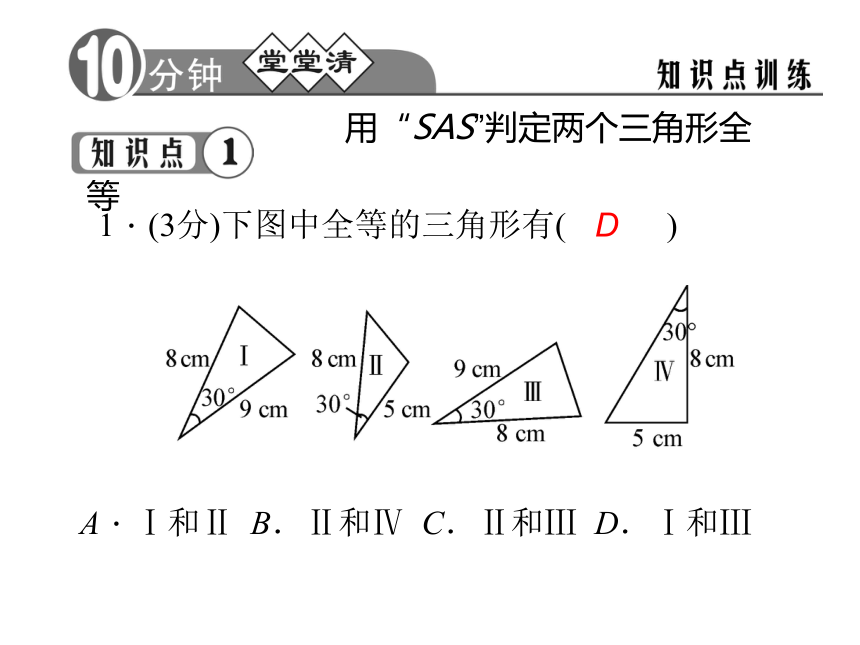
课件21张PPT。12.2 三角形全等的判定第2课时 边角边12.2 三角形全等的判定有两边和它们的 分别相等的两个三角形全等,简写成“ ”或“ ”. 边角边SAS夹角 用“SAS”判定两个三角形全等 1.(3分)下图中全等的三角形有( )
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ D 2.(3分)下列条件中,可以判定△ABC和△A′B′C′全等的是( )
A.BC=BA,B′C′=B′A′,∠B=∠B′
B.∠A=∠B′,AC=A′B′,AB=B′C′
C.∠A=∠A′,AB=B′C′,AC=A′C′
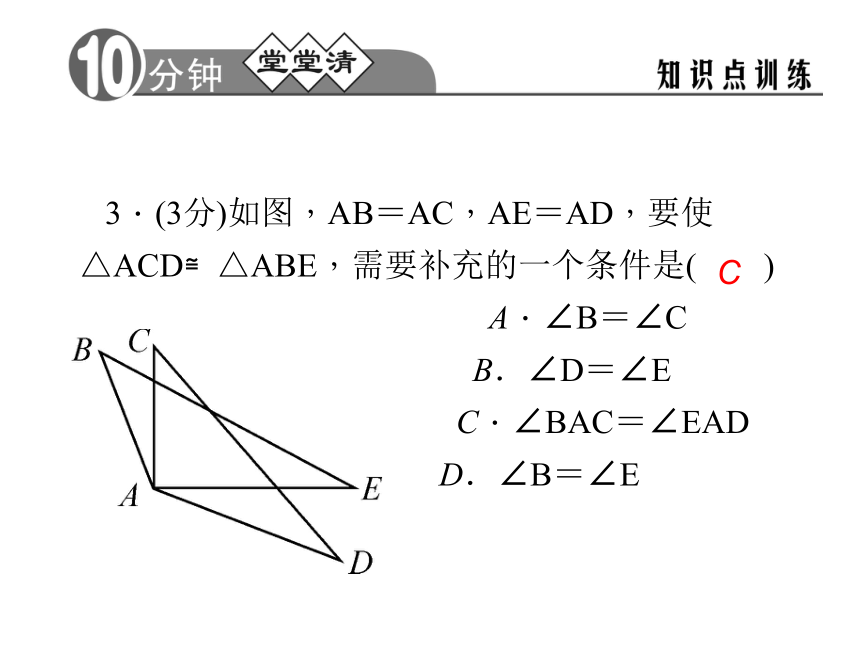
D.BC=B′C′,AC=A′B′,∠B=∠C′B3.(3分)如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
A.∠B=∠C
B.∠D=∠E
C.∠BAC=∠EAD
D.∠B=∠E
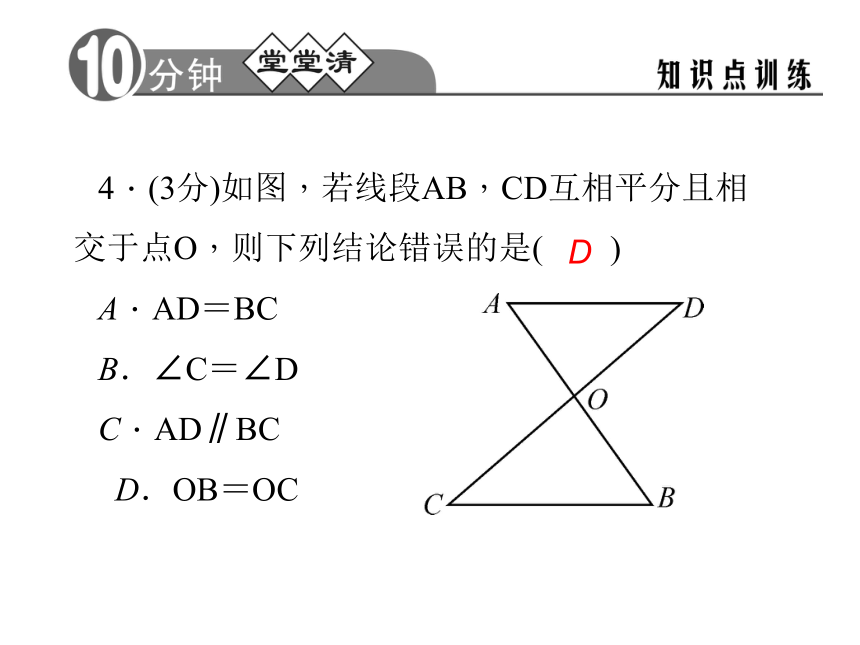
C4.(3分)如图,若线段AB,CD互相平分且相交于点O,则下列结论错误的是( )
A.AD=BC
B.∠C=∠D
C.AD∥BC
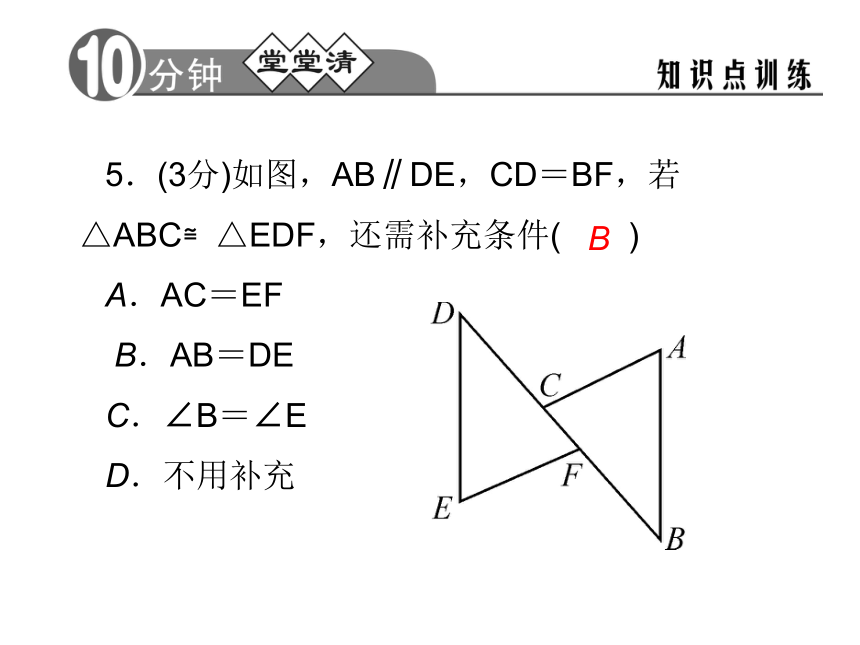
D.OB=OCD5.(3分)如图,AB∥DE,CD=BF,若△ABC≌△EDF,还需补充条件( )
A.AC=EF
B.AB=DE
C.∠B=∠E
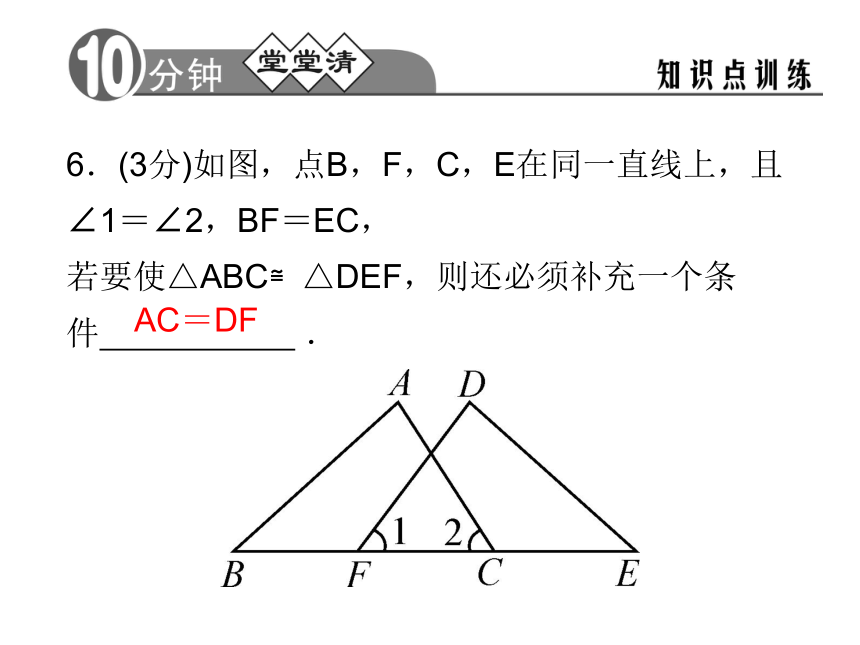
D.不用补充B6.(3分)如图,点B,F,C,E在同一直线上,且∠1=∠2,BF=EC,
若要使△ABC≌△DEF,则还必须补充一个条件 .AC=DF7.(6分)如图,已知,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED,求证:AC=CD.
证明:∵AB∥DE,∴∠B=∠E,又AB=CE,BC=DE,∴△ABC≌△CED(SAS).
∴AC=CD.8.(8分)如图,已知:AB=AD,AC=AE,∠1=∠2,
求证:
(1)△ABC≌△ADE;
(2)∠B=∠D.
解:证明:(1)∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,又∵AB=AD,AC=AE,∴△ABC≌△ADE (2)∵△ABC≌△ADE,∴∠B=∠D9.(8分)如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
证明:∵∠1=∠2,∠AOC=∠DOC,
∴180°-∠1-∠AOE=180°-∠2-∠DOC,即∠E=∠C,又AC=AE,BC=DE,
∴△ABC≌△ADE(SAS),
∴AB=AD.一、选择题(每小题4分,共16分)
10.如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对
B.2对
C.3对
D.4对C 11.如图,AD=AE,BE=CD,∠1=∠2,∠2=110°,∠BAE=60°,那么∠CAE等于( )
A.20°
B.30°
C.40°
D.50°A12.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8
B.7
C.6
D.5B 13.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个D二、填空题(每小题4分,共8分)
14.如图,在△ABC中,AB=BC=CA,∠ABC=∠C=60°,BD=CE,AD与BE相交于点F,则∠AFE= .
, 60°15.如图,已知:在△ABC中,AB=AC,AD是角平分线,BE=CF,有下列说法:①DA平分∠EDF;
②△EBD≌△FCD;
③BD=CD;④AD⊥BC,
其中正确的是 .(填序号)①②③④三、解答题(共36分)
16.(10分)如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD.求证:∠1=∠2.
解:△ABN≌△CDM(SAS),
再证△BMN≌△DNM(SAS)17.(12分)如图,AD=AE,BD=CE,AF⊥BC,且F是BC的中点,求证:∠D=∠E.
证明:连接AB,AC,∵F为BC的中点,∴BF=CF,又∵AF⊥BC,∴∠BFA=∠AFC=90°,在△ABF和△ACF中,
∴△ABF≌△ACF(SAS),∴AB=AC,在△ABD和△ACE中,∴△ABD≌△ACE,∴∠D=∠E【综合运用】18.(14分)两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.求证:CD⊥BE.
解:证△ABE≌△ACD(SAS),得∠ACD=∠ABE=45°,∴∠BCD=∠ACB+∠ACD=45°+45°=90°,即CD⊥BE.
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ D 2.(3分)下列条件中,可以判定△ABC和△A′B′C′全等的是( )
A.BC=BA,B′C′=B′A′,∠B=∠B′
B.∠A=∠B′,AC=A′B′,AB=B′C′
C.∠A=∠A′,AB=B′C′,AC=A′C′
D.BC=B′C′,AC=A′B′,∠B=∠C′B3.(3分)如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
A.∠B=∠C
B.∠D=∠E
C.∠BAC=∠EAD
D.∠B=∠E
C4.(3分)如图,若线段AB,CD互相平分且相交于点O,则下列结论错误的是( )
A.AD=BC
B.∠C=∠D
C.AD∥BC
D.OB=OCD5.(3分)如图,AB∥DE,CD=BF,若△ABC≌△EDF,还需补充条件( )
A.AC=EF
B.AB=DE
C.∠B=∠E
D.不用补充B6.(3分)如图,点B,F,C,E在同一直线上,且∠1=∠2,BF=EC,
若要使△ABC≌△DEF,则还必须补充一个条件 .AC=DF7.(6分)如图,已知,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED,求证:AC=CD.
证明:∵AB∥DE,∴∠B=∠E,又AB=CE,BC=DE,∴△ABC≌△CED(SAS).
∴AC=CD.8.(8分)如图,已知:AB=AD,AC=AE,∠1=∠2,
求证:
(1)△ABC≌△ADE;
(2)∠B=∠D.
解:证明:(1)∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,又∵AB=AD,AC=AE,∴△ABC≌△ADE (2)∵△ABC≌△ADE,∴∠B=∠D9.(8分)如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
证明:∵∠1=∠2,∠AOC=∠DOC,
∴180°-∠1-∠AOE=180°-∠2-∠DOC,即∠E=∠C,又AC=AE,BC=DE,
∴△ABC≌△ADE(SAS),
∴AB=AD.一、选择题(每小题4分,共16分)
10.如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对
B.2对
C.3对
D.4对C 11.如图,AD=AE,BE=CD,∠1=∠2,∠2=110°,∠BAE=60°,那么∠CAE等于( )
A.20°
B.30°
C.40°
D.50°A12.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8
B.7
C.6
D.5B 13.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个D二、填空题(每小题4分,共8分)
14.如图,在△ABC中,AB=BC=CA,∠ABC=∠C=60°,BD=CE,AD与BE相交于点F,则∠AFE= .
, 60°15.如图,已知:在△ABC中,AB=AC,AD是角平分线,BE=CF,有下列说法:①DA平分∠EDF;
②△EBD≌△FCD;
③BD=CD;④AD⊥BC,
其中正确的是 .(填序号)①②③④三、解答题(共36分)
16.(10分)如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD.求证:∠1=∠2.
解:△ABN≌△CDM(SAS),
再证△BMN≌△DNM(SAS)17.(12分)如图,AD=AE,BD=CE,AF⊥BC,且F是BC的中点,求证:∠D=∠E.
证明:连接AB,AC,∵F为BC的中点,∴BF=CF,又∵AF⊥BC,∴∠BFA=∠AFC=90°,在△ABF和△ACF中,
∴△ABF≌△ACF(SAS),∴AB=AC,在△ABD和△ACE中,∴△ABD≌△ACE,∴∠D=∠E【综合运用】18.(14分)两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.求证:CD⊥BE.
解:证△ABE≌△ACD(SAS),得∠ACD=∠ABE=45°,∴∠BCD=∠ACB+∠ACD=45°+45°=90°,即CD⊥BE.
