12.2三角形全等的判定(4)同步习题精讲课件
文档属性
| 名称 | 12.2三角形全等的判定(4)同步习题精讲课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 00:00:00 | ||
图片预览



文档简介
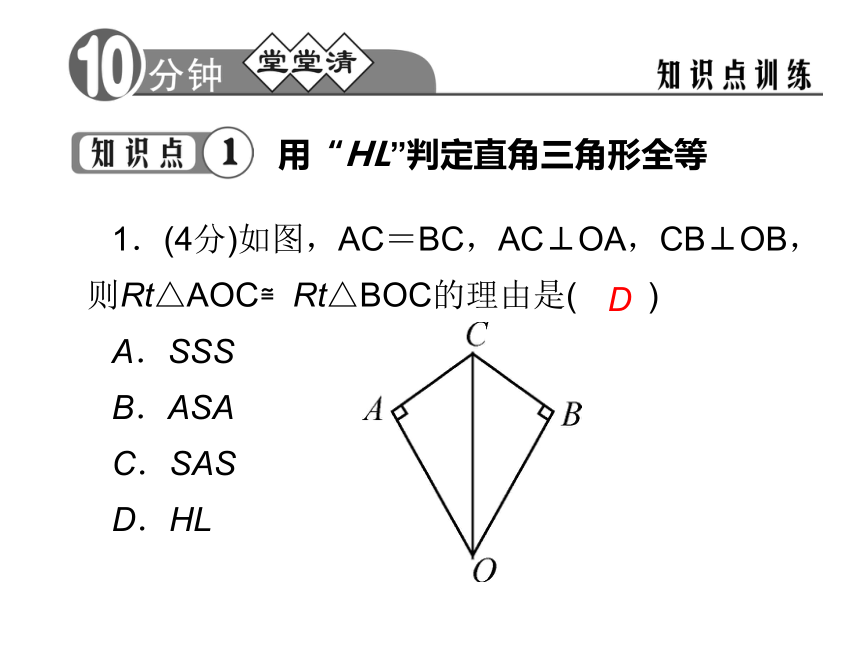
课件20张PPT。12.2 三角形全等的判定第4课时 斜边、直角边12.2 三角形全等的判定斜边和一条直角边分别相等的两个直角三角形 ,简写成“ ”或“ ”. 全等斜边、直角边HL 用“HL”判定直角三角形全等1.(4分)如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS
B.ASA
C.SAS
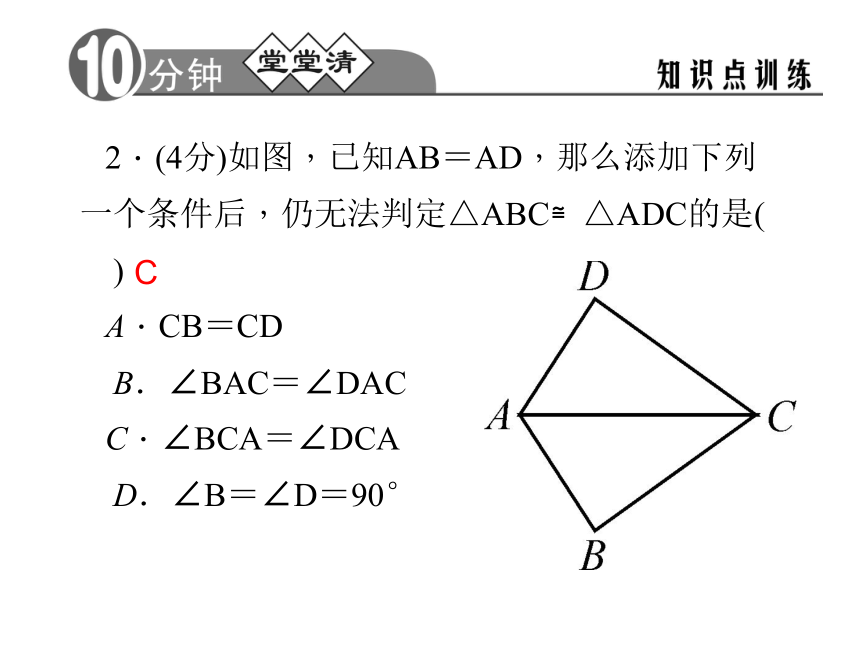
D.HLD 2.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
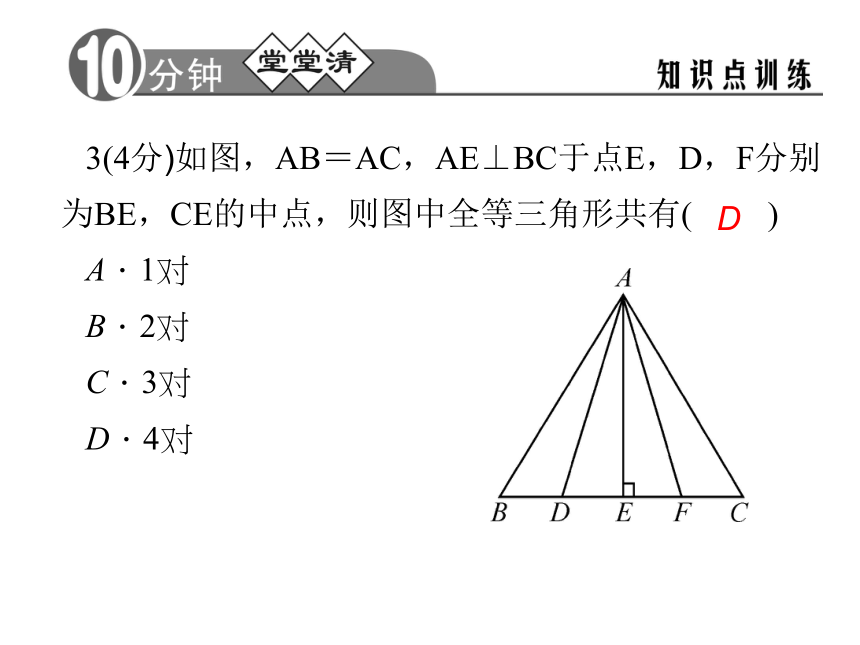
C 3(4分)如图,AB=AC,AE⊥BC于点E,D,F分别为BE,CE的中点,则图中全等三角形共有( )
A.1对
B.2对
C.3对
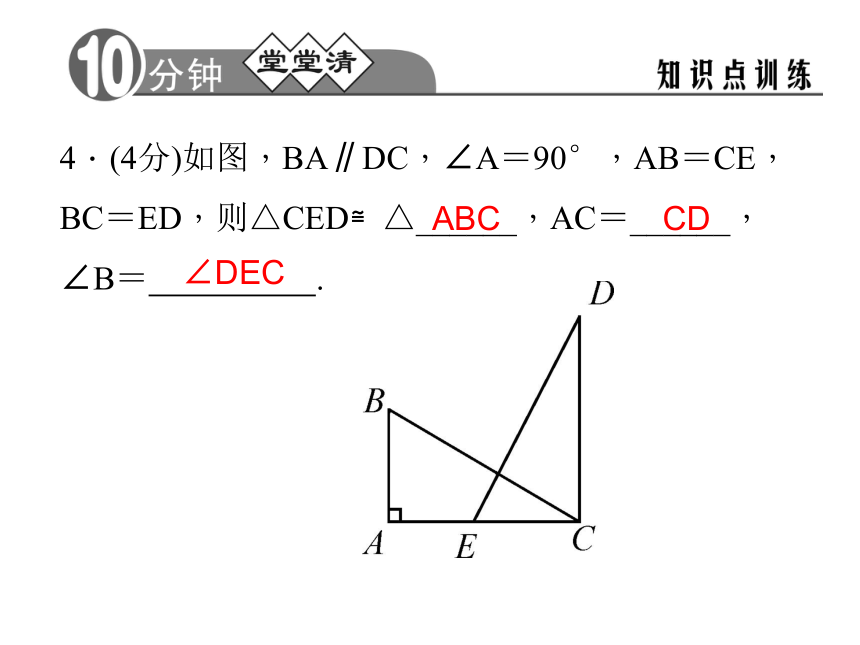
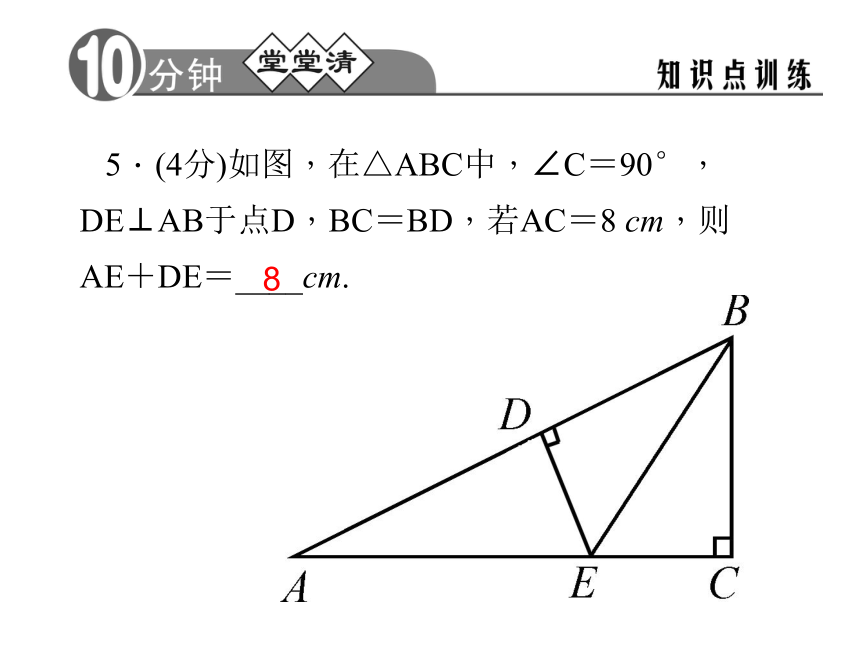
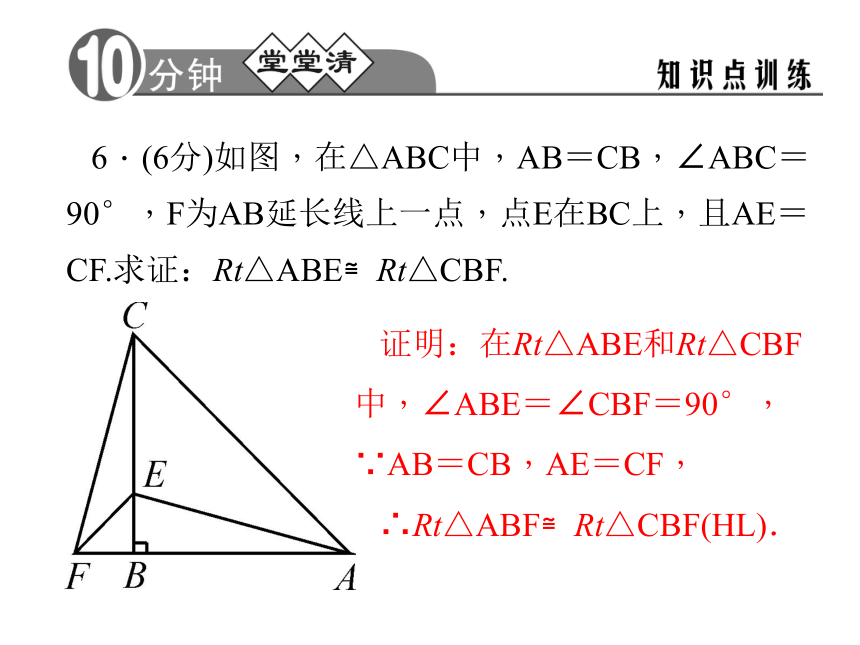
D.4对 D4.(4分)如图,BA∥DC,∠A=90°,AB=CE,BC=ED,则△CED≌△______,AC=______,∠B= .ABCCD∠DEC 5.(4分)如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD,若AC=8 cm,则AE+DE=____cm.86.(6分)如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.证明:在Rt△ABE和Rt△CBF中,∠ABE=∠CBF=90°,∵AB=CB,AE=CF,
∴Rt△ABF≌Rt△CBF(HL).7.(6分)如图,已知AD为△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,
求证:BE⊥AC.
证明:∵AD⊥BC,∴∠BDA=∠ADC=90°,又BF=AC,FD=CD,
∴Rt△BFD≌Rt△ACD(HL),∴∠2=∠C,又∠1+∠2=90°,∴∠1+∠C=90°,∴BE⊥AC.8.(8分)如图,已知AE⊥BC,DF⊥BC,E,F是垂足,AE=DF,AB=DC,求证:AC=DB.
证明:AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°.在Rt△ABE和Rt△DCF中,,∴Rt△ABE≌Rt△DCF(HL),∴∠ABC=∠DCB.在△ABC和△DCB中,∴△ABC≌△DCB(SAS),
∴AC=DB 一、选择题(每小题5分,共20分)
9.在下列结论中,正确的个数有( )
①在Rt△ABC中,两锐角互余;②有一锐角和一边对应相等的两个直角三角形全等;③斜边对应相等的两个等腰直角三角形全等;④所有的直角三角形都全等.
A.1个 B.2个 C.3个 D.4个C 10.如图,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列三个结论( )
①AS=AR;②QP∥AR;③△BRP≌△QSP.
A.全部正确
B.仅①和②正确
C.仅①正确
D.仅①和③正确B 11.如图,将长方形纸片ABCD沿BD折叠得到△BDC′,图中(包含实线和虚线)共有全等三角形( )
A.2对
B.3对
C.4对
D.5对C12.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,添加下列条件能使△AEH≌△CEB的有( )
①AE=EC;②AH=BC;③EH=BE;
④∠EAH=∠B.
A.①②④ B.①②③
C.②③④ D.①③④B二、填空题(每小题5分,共20分)
13.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
55°14.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O,则图中全等三角形共有____对.
15.如图,∠A=∠D=90°,AC=DB,欲证OB=OC,可以先利用“HL”证明 ,再利用“ ”证明△AOB≌ 得到OB=OC.3Rt△ABC≌Rt△DCBAAS△DOC16.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,若CE=2,BD=6,则DE=____.8三、解答题(共20分)
17.(8分)如图,∠ACB=∠ADB=90°,AC=AD,点E在AB上,求证:CE=DE.
证明:Rt△ACB和Rt△ADB中,
∵∠ACB=∠ADB=90°
∴Rt△ACB≌Rt△ADB(HL),
∴∠1=∠2.在△ACE和△ADE中,∴△ACE≌△ADE,∴CE=DE.【综合运用】18.(12分)如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形?请你一一列举;
(2)求证:CF=EF.解:(1)△ADC≌△ABE,△CDF≌△EBF.
(2)连接AF,∵Rt△ABC≌Rt△ADE,∴AB=AD,BC=DE,∠ABC=∠ADE=90°,又∵AF=AF,∴Rt△ABF≌Rt△ADF(HL),∴BF=DF.又BC=DE,∴BC-BF=DF-DF即CF=EF.
A.SSS
B.ASA
C.SAS
D.HLD 2.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
C 3(4分)如图,AB=AC,AE⊥BC于点E,D,F分别为BE,CE的中点,则图中全等三角形共有( )
A.1对
B.2对
C.3对
D.4对 D4.(4分)如图,BA∥DC,∠A=90°,AB=CE,BC=ED,则△CED≌△______,AC=______,∠B= .ABCCD∠DEC 5.(4分)如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD,若AC=8 cm,则AE+DE=____cm.86.(6分)如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.证明:在Rt△ABE和Rt△CBF中,∠ABE=∠CBF=90°,∵AB=CB,AE=CF,
∴Rt△ABF≌Rt△CBF(HL).7.(6分)如图,已知AD为△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,
求证:BE⊥AC.
证明:∵AD⊥BC,∴∠BDA=∠ADC=90°,又BF=AC,FD=CD,
∴Rt△BFD≌Rt△ACD(HL),∴∠2=∠C,又∠1+∠2=90°,∴∠1+∠C=90°,∴BE⊥AC.8.(8分)如图,已知AE⊥BC,DF⊥BC,E,F是垂足,AE=DF,AB=DC,求证:AC=DB.
证明:AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°.在Rt△ABE和Rt△DCF中,,∴Rt△ABE≌Rt△DCF(HL),∴∠ABC=∠DCB.在△ABC和△DCB中,∴△ABC≌△DCB(SAS),
∴AC=DB 一、选择题(每小题5分,共20分)
9.在下列结论中,正确的个数有( )
①在Rt△ABC中,两锐角互余;②有一锐角和一边对应相等的两个直角三角形全等;③斜边对应相等的两个等腰直角三角形全等;④所有的直角三角形都全等.
A.1个 B.2个 C.3个 D.4个C 10.如图,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列三个结论( )
①AS=AR;②QP∥AR;③△BRP≌△QSP.
A.全部正确
B.仅①和②正确
C.仅①正确
D.仅①和③正确B 11.如图,将长方形纸片ABCD沿BD折叠得到△BDC′,图中(包含实线和虚线)共有全等三角形( )
A.2对
B.3对
C.4对
D.5对C12.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,添加下列条件能使△AEH≌△CEB的有( )
①AE=EC;②AH=BC;③EH=BE;
④∠EAH=∠B.
A.①②④ B.①②③
C.②③④ D.①③④B二、填空题(每小题5分,共20分)
13.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
55°14.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点O,则图中全等三角形共有____对.
15.如图,∠A=∠D=90°,AC=DB,欲证OB=OC,可以先利用“HL”证明 ,再利用“ ”证明△AOB≌ 得到OB=OC.3Rt△ABC≌Rt△DCBAAS△DOC16.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,若CE=2,BD=6,则DE=____.8三、解答题(共20分)
17.(8分)如图,∠ACB=∠ADB=90°,AC=AD,点E在AB上,求证:CE=DE.
证明:Rt△ACB和Rt△ADB中,
∵∠ACB=∠ADB=90°
∴Rt△ACB≌Rt△ADB(HL),
∴∠1=∠2.在△ACE和△ADE中,∴△ACE≌△ADE,∴CE=DE.【综合运用】18.(12分)如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形?请你一一列举;
(2)求证:CF=EF.解:(1)△ADC≌△ABE,△CDF≌△EBF.
(2)连接AF,∵Rt△ABC≌Rt△ADE,∴AB=AD,BC=DE,∠ABC=∠ADE=90°,又∵AF=AF,∴Rt△ABF≌Rt△ADF(HL),∴BF=DF.又BC=DE,∴BC-BF=DF-DF即CF=EF.
