《角的平分线的性质》同步练习(1)及答案
文档属性
| 名称 | 《角的平分线的性质》同步练习(1)及答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 23.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 00:00:00 | ||
图片预览


文档简介
角的平分线的性质
知识点1:角平分线的性质
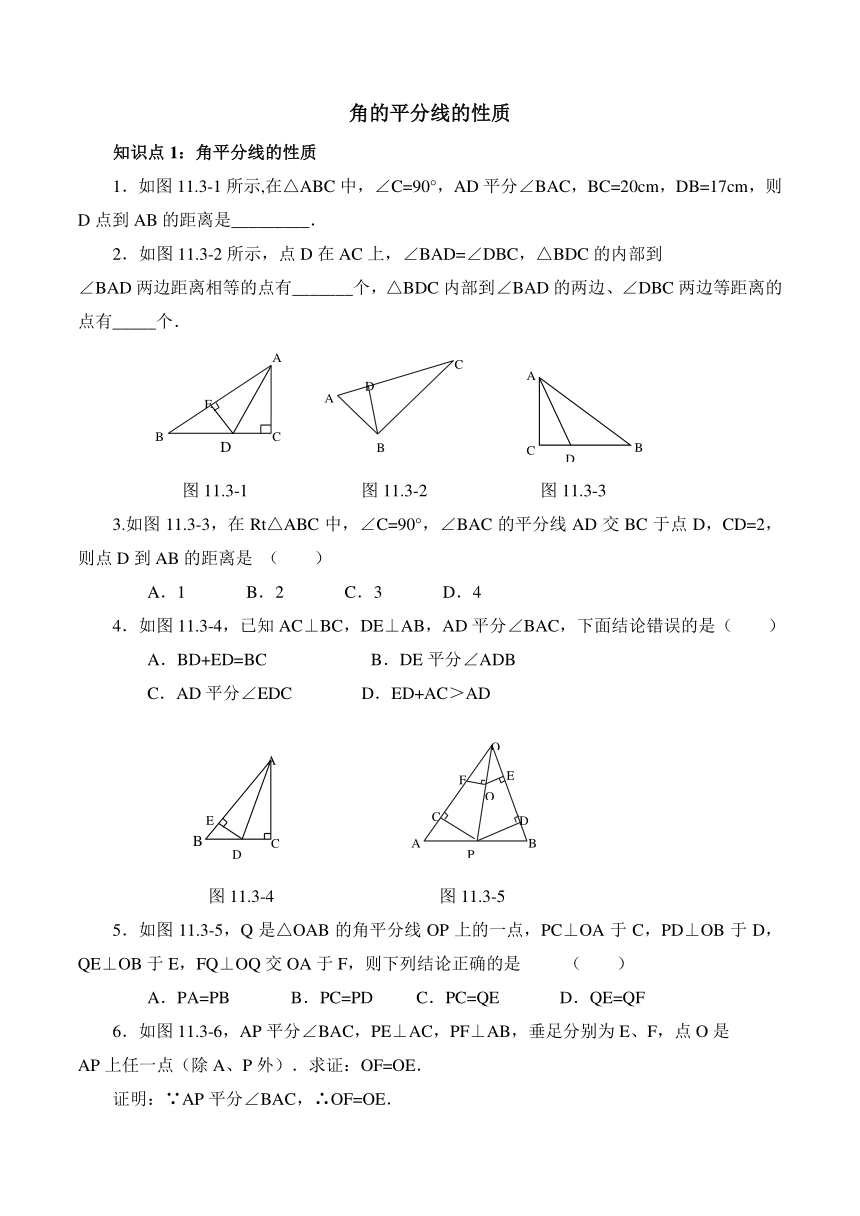
1.如图11.3-1所示,在△ABC中,∠C=90°,AD平分∠BAC,BC=20cm,DB=17cm,则D点到AB的距离是_________.
2.如图11.3-2所示,点D在AC上,∠BAD=∠DBC,△BDC的内部到
∠BAD两边距离相等的点有_______个,△BDC内部到∠BAD的两边、∠DBC两边等距离的点有_____个.
图11.3-1 图11.3-2 图11.3-3
3.如图11.3-3,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=2,则点D到AB的距离是 ( )
A.1 B.2 C.3 D.4
4.如图11.3-4,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
A.BD+ED=BC B.DE平分∠ADB
C.AD平分∠EDC D.ED+AC>AD
图11.3-4 图11.3-5
5.如图11.3-5,Q是△OAB的角平 ( http: / / www.21cnjy.com )分线OP上的一点,PC⊥OA于C,PD⊥OB于D,QE⊥OB于E,FQ⊥OQ交OA于F,则下列结论正确的是 ( )
A.PA=PB B.PC=PD C.PC=QE D.QE=QF
6.如图11.3-6,AP平分∠BAC,PE⊥AC,PF⊥AB,垂足分别为E、F,点O是
AP上任一点(除A、P外).求证:OF=OE.
证明:∵AP平分∠BAC,∴OF=OE.
以上证明过程是否正确?若不正确,请改正.
7.如图11.3-7,在△ABC中,∠C=90°,AD平分∠BAC,D到AB的距离为12,
BD∶DC=5∶3.试求BC的长.
知识点2:角平分线的性质与判定的综合应用
8.如图11.3-8,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD
=_______,∠CAD=____.
9.如图11.3-9,已知点C是∠AOB的 ( http: / / www.21cnjy.com )平分线上一点,点P、P′分别在边OA、OB上,若要得到OP=OP′,需要添加以下条件中某一个即可,请你写出所有可能结果的序号:______________.
①∠OCP=∠OCP′;②∠OPC=∠OPC′;③PC=PC′;④PP′⊥OC.
图11.3-8 图11.3-9
10.如图11.3-10,已知AB∥CD, ( http: / / www.21cnjy.com )PE⊥AB,PF⊥BD,PG⊥CD,垂足分别E、F、G,且PF=PG=PE,则∠BPD=________.
11.如图11.3-11,已知DB⊥AE于B,DC⊥AF于C,且DB=DC,∠BAC=
40°,∠ADG=130°,则∠DGF=________.
图11.3-10 图11.3-11
12.与相交的两直线距离相等的点是在 ( )
A.一条射线上 B.一条直线上
C.两条互相垂直的直线上 D.以上都不对
13.下列结论中,错误的是 ( )
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
14.如图11.3-12,已知BD平分∠ABC,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M、N为垂足.求证:PM=PN.
15.如图11.3-13,AD⊥DC,BC⊥DC,E是DC上一点,AE平分∠DAB.
(1)如果BE平分∠ABC,求证:点E是DC的中点;
(2)如果E是DC的中点,求证:BE平分∠ABC.
参考答案
1.3cm[点拨:由角平分线性质,得DE=DC=BC-DB=20-17=3(cm)]
2.无数;1
3.B(点拨:点D到AB的距离等于DC)
4.C
5.B(点拨:只有PC、PD都是角平分线上的点到角两边的距离)
6.不正确.AP平分∠BAC,PF⊥AB,PE⊥AC,∴PF=PE,接着证△APE≌△APF,得AE=AF,再证△AOF≌△AOE即可.
7.由题意,得DC=12,BC=DC=×12=32.
8.40°;40°(点拨:由BD=DC,DB⊥AB,DC⊥AC,得DA平分∠BAC,所以∠BAD=∠CAD=∠BAC=40°)
9.①②④(点拨:SSA不能判定两个三角形全等)
10.90°(点拨:由PE=PF得∠PBD=∠ABD,由PF=PG得∠PDB=∠BDC.由AB//CD,得∠ABD+∠BDC=180°,∴∠PBD+∠PDB=×180°=90°,∠BPD=90°)
11.150°(点拨:由DB=DC得∠GAD=∠BAD=∠BAC=20°,∠DGF=∠GAD+∠ADG=130+20°=150°)
12.C(点拨:相交的两直线有两对对顶角)
13.B
14.先证△ABD≌△CBD,得∠ADB=∠CDB,由PM⊥AD,PN⊥CD,得PM=PN.
15.(1)如右图,过点E ( http: / / www.21cnjy.com )作EF⊥AB,F为垂足.由角平分线性质得ED=EF,EF=EC,∴ED=EC,即点E是DC的中点 ;(2)过点E作EF⊥AB,F为垂足.由角平分线性质得ED=EF,又ED=EC,∴EF=EC,由角平分线的得和是BE平分∠ABC.
B
C
D
A
E
A
D
C
B
A
C
B
D
A
O
B
P
C
D
F
E
Q
A
B
C
D
E
B
A
E
C
P
O
F
图13.3-6
A
B
C
D
图13.3-7
A
B
C
D
A
B
O
P
C
P′
A
B
C
D
P
F
E
G
F
B
D
A
C
G
A
B
D
P
M
N
C
图13.3-12
A
D
B
C
E
图13.3-13
A
D
B
C
F
E
知识点1:角平分线的性质
1.如图11.3-1所示,在△ABC中,∠C=90°,AD平分∠BAC,BC=20cm,DB=17cm,则D点到AB的距离是_________.
2.如图11.3-2所示,点D在AC上,∠BAD=∠DBC,△BDC的内部到
∠BAD两边距离相等的点有_______个,△BDC内部到∠BAD的两边、∠DBC两边等距离的点有_____个.
图11.3-1 图11.3-2 图11.3-3
3.如图11.3-3,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=2,则点D到AB的距离是 ( )
A.1 B.2 C.3 D.4
4.如图11.3-4,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
A.BD+ED=BC B.DE平分∠ADB
C.AD平分∠EDC D.ED+AC>AD
图11.3-4 图11.3-5
5.如图11.3-5,Q是△OAB的角平 ( http: / / www.21cnjy.com )分线OP上的一点,PC⊥OA于C,PD⊥OB于D,QE⊥OB于E,FQ⊥OQ交OA于F,则下列结论正确的是 ( )
A.PA=PB B.PC=PD C.PC=QE D.QE=QF
6.如图11.3-6,AP平分∠BAC,PE⊥AC,PF⊥AB,垂足分别为E、F,点O是
AP上任一点(除A、P外).求证:OF=OE.
证明:∵AP平分∠BAC,∴OF=OE.
以上证明过程是否正确?若不正确,请改正.
7.如图11.3-7,在△ABC中,∠C=90°,AD平分∠BAC,D到AB的距离为12,
BD∶DC=5∶3.试求BC的长.
知识点2:角平分线的性质与判定的综合应用
8.如图11.3-8,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD
=_______,∠CAD=____.
9.如图11.3-9,已知点C是∠AOB的 ( http: / / www.21cnjy.com )平分线上一点,点P、P′分别在边OA、OB上,若要得到OP=OP′,需要添加以下条件中某一个即可,请你写出所有可能结果的序号:______________.
①∠OCP=∠OCP′;②∠OPC=∠OPC′;③PC=PC′;④PP′⊥OC.
图11.3-8 图11.3-9
10.如图11.3-10,已知AB∥CD, ( http: / / www.21cnjy.com )PE⊥AB,PF⊥BD,PG⊥CD,垂足分别E、F、G,且PF=PG=PE,则∠BPD=________.
11.如图11.3-11,已知DB⊥AE于B,DC⊥AF于C,且DB=DC,∠BAC=
40°,∠ADG=130°,则∠DGF=________.
图11.3-10 图11.3-11
12.与相交的两直线距离相等的点是在 ( )
A.一条射线上 B.一条直线上
C.两条互相垂直的直线上 D.以上都不对
13.下列结论中,错误的是 ( )
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
14.如图11.3-12,已知BD平分∠ABC,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M、N为垂足.求证:PM=PN.
15.如图11.3-13,AD⊥DC,BC⊥DC,E是DC上一点,AE平分∠DAB.
(1)如果BE平分∠ABC,求证:点E是DC的中点;
(2)如果E是DC的中点,求证:BE平分∠ABC.
参考答案
1.3cm[点拨:由角平分线性质,得DE=DC=BC-DB=20-17=3(cm)]
2.无数;1
3.B(点拨:点D到AB的距离等于DC)
4.C
5.B(点拨:只有PC、PD都是角平分线上的点到角两边的距离)
6.不正确.AP平分∠BAC,PF⊥AB,PE⊥AC,∴PF=PE,接着证△APE≌△APF,得AE=AF,再证△AOF≌△AOE即可.
7.由题意,得DC=12,BC=DC=×12=32.
8.40°;40°(点拨:由BD=DC,DB⊥AB,DC⊥AC,得DA平分∠BAC,所以∠BAD=∠CAD=∠BAC=40°)
9.①②④(点拨:SSA不能判定两个三角形全等)
10.90°(点拨:由PE=PF得∠PBD=∠ABD,由PF=PG得∠PDB=∠BDC.由AB//CD,得∠ABD+∠BDC=180°,∴∠PBD+∠PDB=×180°=90°,∠BPD=90°)
11.150°(点拨:由DB=DC得∠GAD=∠BAD=∠BAC=20°,∠DGF=∠GAD+∠ADG=130+20°=150°)
12.C(点拨:相交的两直线有两对对顶角)
13.B
14.先证△ABD≌△CBD,得∠ADB=∠CDB,由PM⊥AD,PN⊥CD,得PM=PN.
15.(1)如右图,过点E ( http: / / www.21cnjy.com )作EF⊥AB,F为垂足.由角平分线性质得ED=EF,EF=EC,∴ED=EC,即点E是DC的中点 ;(2)过点E作EF⊥AB,F为垂足.由角平分线性质得ED=EF,又ED=EC,∴EF=EC,由角平分线的得和是BE平分∠ABC.
B
C
D
A
E
A
D
C
B
A
C
B
D
A
O
B
P
C
D
F
E
Q
A
B
C
D
E
B
A
E
C
P
O
F
图13.3-6
A
B
C
D
图13.3-7
A
B
C
D
A
B
O
P
C
P′
A
B
C
D
P
F
E
G
F
B
D
A
C
G
A
B
D
P
M
N
C
图13.3-12
A
D
B
C
E
图13.3-13
A
D
B
C
F
E
