12.3角的平分线的性质(1)同步习题精讲课件
文档属性
| 名称 | 12.3角的平分线的性质(1)同步习题精讲课件 |  | |
| 格式 | zip | ||
| 文件大小 | 290.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 14:36:46 | ||
图片预览




文档简介
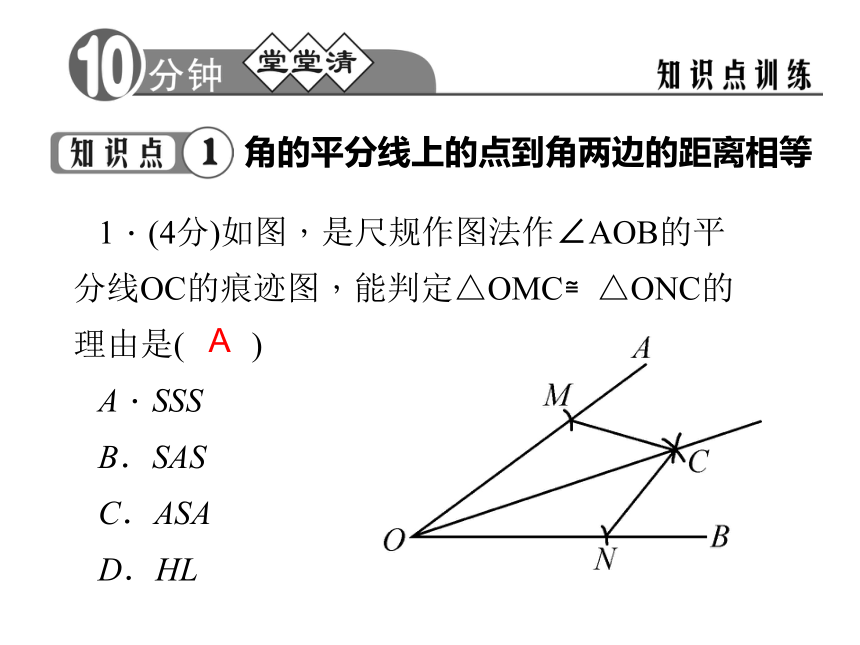
课件20张PPT。12.3 角的平分线的性质 第1课时 角的平分线的性质12.2 三角形全等的判定角的平分线上的点到角的两边的距离____.相等角的平分线上的点到角两边的距离相等 1.(4分)如图,是尺规作图法作∠AOB的平分线OC的痕迹图,能判定△OMC≌△ONC的理由是( )
A.SSS
B.SAS
C.ASA
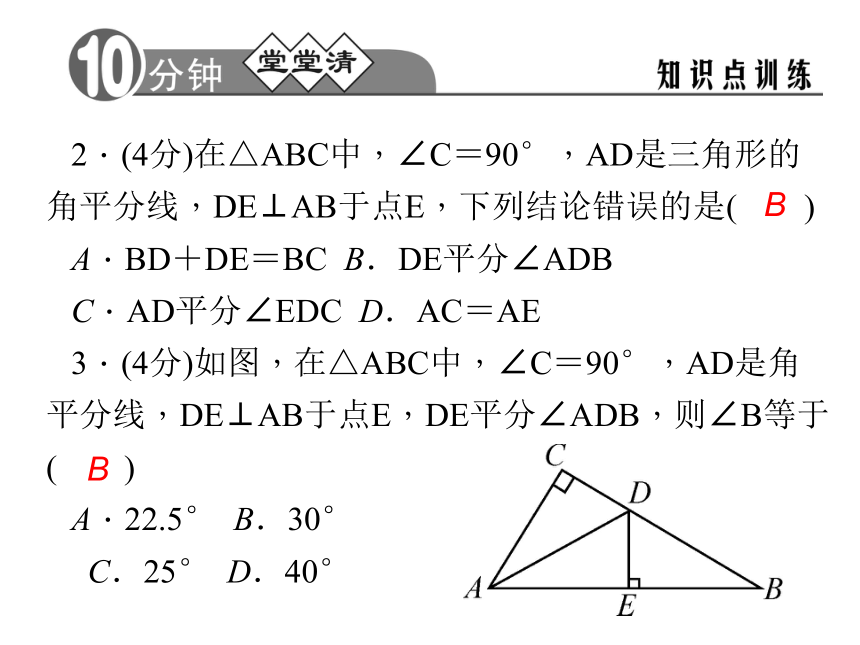
D.HLA 2.(4分)在△ABC中,∠C=90°,AD是三角形的角平分线,DE⊥AB于点E,下列结论错误的是( )
A.BD+DE=BC B.DE平分∠ADB
C.AD平分∠EDC D.AC=AE
3.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于点E,DE平分∠ADB,则∠B等于( )
A.22.5° B.30°
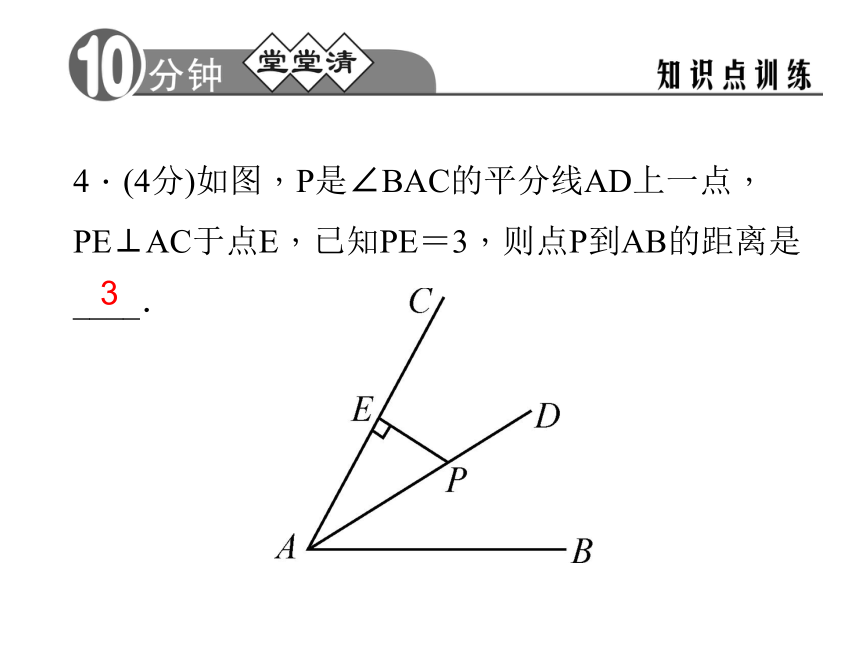
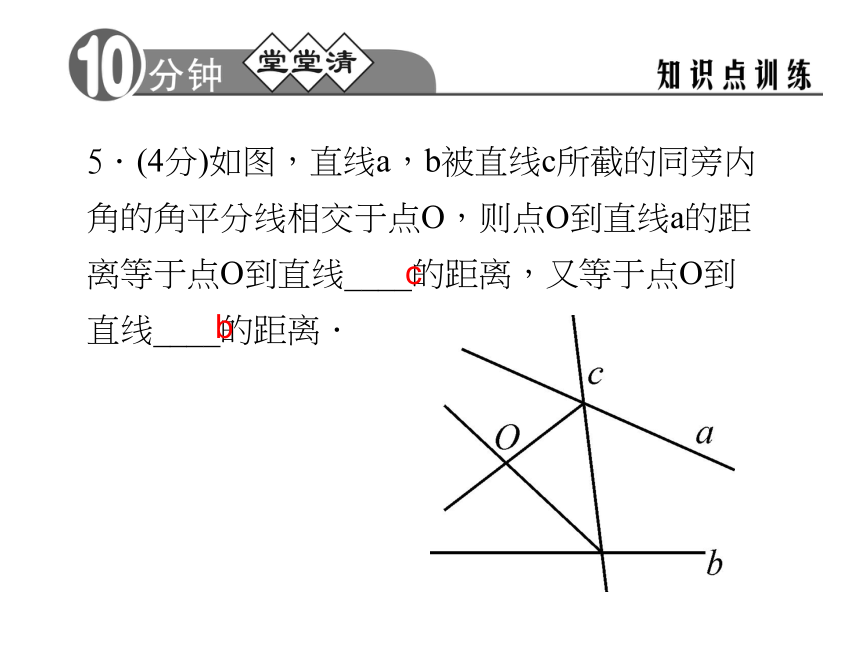
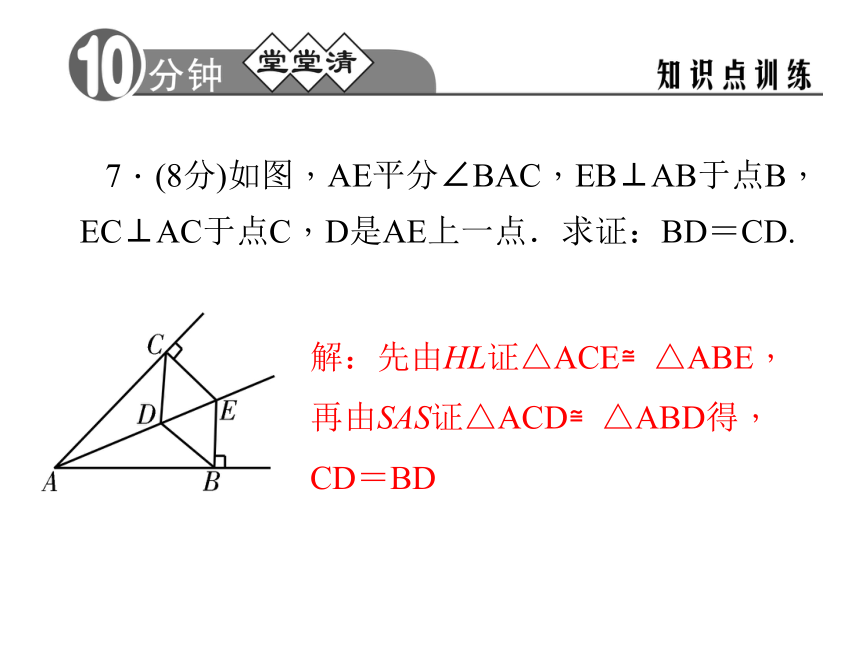
C.25° D.40°BB4.(4分)如图,P是∠BAC的平分线AD上一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是____.35.(4分)如图,直线a,b被直线c所截的同旁内角的角平分线相交于点O,则点O到直线a的距离等于点O到直线____的距离,又等于点O到直线____的距离.cb 6.(4分)如图,BD是∠ABC的平分线,DE⊥AB于点E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,则DE= . 6 cm7.(8分)如图,AE平分∠BAC,EB⊥AB于点B,EC⊥AC于点C,D是AE上一点.求证:BD=CD.
解:先由HL证△ACE≌△ABE,
再由SAS证△ACD≌△ABD得,
CD=BD 8.(8分)如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,又∵OA=OB,OD=OD,∴△AOD≌△BOD,∴∠3=∠4,又∵PM⊥DB,PN⊥DA,∴PM=PN(角平分线上的点到角两边的距离相等).一、选择题(每小题5分,共25分)
9.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠CPO=∠DPO D.OC=PC
, D 10.如图,在△ABC中,∠B,∠C的平分线交于点O,OD⊥AB于点D,OE⊥AC于点E,则OD与OE的大小关系是( )
A.OD>OE B.OD=OE
C.ODA.1 B.2 C. 3 D.4
12.如图,已知AB∥CD,O是∠ACD,∠CAB的平分线的交点,且OE⊥AC于点E,OE=12,则AB与CD之间的距离为( )
A.12 B.18
C.24 D.无法确定BC 13.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP D二、填空题(每小题5分,共15分)
14.如图,在△ABC中,AD是∠BAC的角平分线,AB=6 cm,AC=8 cm,则S△ABD∶S△ACD=____,BD∶CD= .3∶43∶415.如图,已知点E是∠AOB平分线上一点,点C,D分别在边OA,OB上,如果要得到OC=OD,需要添加以下条件中的某一个即可:①∠OEC=∠OED;②∠OCE=∠ODE;③CE=DE;④CD⊥OE,请你写出所有可能结果的序号 .①②④ 如图△ABC中∠B=47°,三角形外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .66.5°三、解答题(共20分)
17.(8分)如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=(AB+AD).
证明:过点C作点CF⊥AD,
交AD延 长线于点F,易证△CEB≌△CFD,△AEC≌△AFC,∴DF=BE,AF=AE,又DF=AF-AD=AE-AD,BE=AB-AE,∴AB-AE=AE-AD即AE= (AB+AD)【综合运用】18.(12分)如图,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是CD的中点,问AD,BC与AB之间有何关系?并证明你的结论.证明:AD+BC=AB.过点E作EF⊥AB于F,连接BE.∵AE平分∠BAD,DC⊥AD,EF⊥AB,∴EF=ED.在Rt△AFE和Rt△ADE中, ∴Rt△AFE≌Rt△ADE(HL),∴AF=AD.∵E是DC的中点,∴DE=EC,∴EC=EF.∵AD∥BC,DC⊥AD,∴DC⊥BC,∴∠DCB=90°.在Rt△BFE和Rt△BCE中,
∴Rt△BFE≌Rt△BCE(HL).∴BF=BC.
∴AD+BC=AF+BF=AB
A.SSS
B.SAS
C.ASA
D.HLA 2.(4分)在△ABC中,∠C=90°,AD是三角形的角平分线,DE⊥AB于点E,下列结论错误的是( )
A.BD+DE=BC B.DE平分∠ADB
C.AD平分∠EDC D.AC=AE
3.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于点E,DE平分∠ADB,则∠B等于( )
A.22.5° B.30°
C.25° D.40°BB4.(4分)如图,P是∠BAC的平分线AD上一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是____.35.(4分)如图,直线a,b被直线c所截的同旁内角的角平分线相交于点O,则点O到直线a的距离等于点O到直线____的距离,又等于点O到直线____的距离.cb 6.(4分)如图,BD是∠ABC的平分线,DE⊥AB于点E,S△ABC=90 cm2,AB=18 cm,BC=12 cm,则DE= . 6 cm7.(8分)如图,AE平分∠BAC,EB⊥AB于点B,EC⊥AC于点C,D是AE上一点.求证:BD=CD.
解:先由HL证△ACE≌△ABE,
再由SAS证△ACD≌△ABD得,
CD=BD 8.(8分)如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,又∵OA=OB,OD=OD,∴△AOD≌△BOD,∴∠3=∠4,又∵PM⊥DB,PN⊥DA,∴PM=PN(角平分线上的点到角两边的距离相等).一、选择题(每小题5分,共25分)
9.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠CPO=∠DPO D.OC=PC
, D 10.如图,在△ABC中,∠B,∠C的平分线交于点O,OD⊥AB于点D,OE⊥AC于点E,则OD与OE的大小关系是( )
A.OD>OE B.OD=OE
C.OD
12.如图,已知AB∥CD,O是∠ACD,∠CAB的平分线的交点,且OE⊥AC于点E,OE=12,则AB与CD之间的距离为( )
A.12 B.18
C.24 D.无法确定BC 13.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP D二、填空题(每小题5分,共15分)
14.如图,在△ABC中,AD是∠BAC的角平分线,AB=6 cm,AC=8 cm,则S△ABD∶S△ACD=____,BD∶CD= .3∶43∶415.如图,已知点E是∠AOB平分线上一点,点C,D分别在边OA,OB上,如果要得到OC=OD,需要添加以下条件中的某一个即可:①∠OEC=∠OED;②∠OCE=∠ODE;③CE=DE;④CD⊥OE,请你写出所有可能结果的序号 .①②④ 如图△ABC中∠B=47°,三角形外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .66.5°三、解答题(共20分)
17.(8分)如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=(AB+AD).
证明:过点C作点CF⊥AD,
交AD延 长线于点F,易证△CEB≌△CFD,△AEC≌△AFC,∴DF=BE,AF=AE,又DF=AF-AD=AE-AD,BE=AB-AE,∴AB-AE=AE-AD即AE= (AB+AD)【综合运用】18.(12分)如图,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是CD的中点,问AD,BC与AB之间有何关系?并证明你的结论.证明:AD+BC=AB.过点E作EF⊥AB于F,连接BE.∵AE平分∠BAD,DC⊥AD,EF⊥AB,∴EF=ED.在Rt△AFE和Rt△ADE中, ∴Rt△AFE≌Rt△ADE(HL),∴AF=AD.∵E是DC的中点,∴DE=EC,∴EC=EF.∵AD∥BC,DC⊥AD,∴DC⊥BC,∴∠DCB=90°.在Rt△BFE和Rt△BCE中,
∴Rt△BFE≌Rt△BCE(HL).∴BF=BC.
∴AD+BC=AF+BF=AB
