专题11 椭圆的简单几何性质-【夯实基础】2023-2024高二数学同步限时训练(人教A版2019选择性必修第一册)(含解析)
文档属性
| 名称 | 专题11 椭圆的简单几何性质-【夯实基础】2023-2024高二数学同步限时训练(人教A版2019选择性必修第一册)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【夯实基础】2023-2024高二数学同步限时训练(新人教A版2019)专题11 椭圆的简单几何性质
一、单选题
1.椭圆的焦距为( )
A. B. C. D.
2.椭圆的长轴长、短轴长和焦点坐标依次为( ).
A.,,B.,,C.,, D.,,
3.已知,分别为椭圆的两个焦点,P为椭圆上一点,则的最大值为( )
A.2 B. C.4 D.
4.已知椭圆C:上的动点P到右焦点距离的最小值为,则( )
A.1 B. C. D.
5.如果椭圆的离心率为,则( )
A. B.或 C. D.或
6.已知椭圆的焦距为2,离心率,则椭圆的标准方程为( )
A. B. C. D.
7.已知椭圆的焦距是2,则离心率e的值是( )
A. B.或 C.或 D.或
8.若椭圆与椭圆,则两椭圆必定( ).
A.有相等的长轴长 B.有相等的焦距
C.有相等的短轴长 D.长轴长与焦距之比相等
9.已知椭圆与,则两个椭圆( )
A.有相同的长轴与短轴 B.有相同的焦距
C.有相同的焦点 D.有相同的离心率
10.中心在原点,焦点在坐标轴上,离心率为,且过点的椭圆方程是( )
A. B.或
C. D.或
11.焦点在轴上,长轴长为10,离心率为的椭圆的标准方程为( )
A. B.
C. D.
12.已知椭圆的离心率为,分别为C的左、右顶点,B为C的上顶点.若,则C的方程为( )
A. B. C. D.
13.设是椭圆的离心率,且,则实数的取值范围是
A. B.
C. D.
14.若椭圆的离心率为,则的值为( )
A. B. C.或 D.或
15.椭圆的左顶点为,点均在上,且关于原点对称.若直线的斜率之积为,则的离心率为( )
A. B. C. D.
16.与椭圆有相同的焦点,且短半轴长为的椭圆方程是( )
A. B. C. D.
17.离心率和椭圆形状的有关,据此判断椭圆和,则和哪个图形更为扁平( )
A. B.
C.相同 D.无法判断
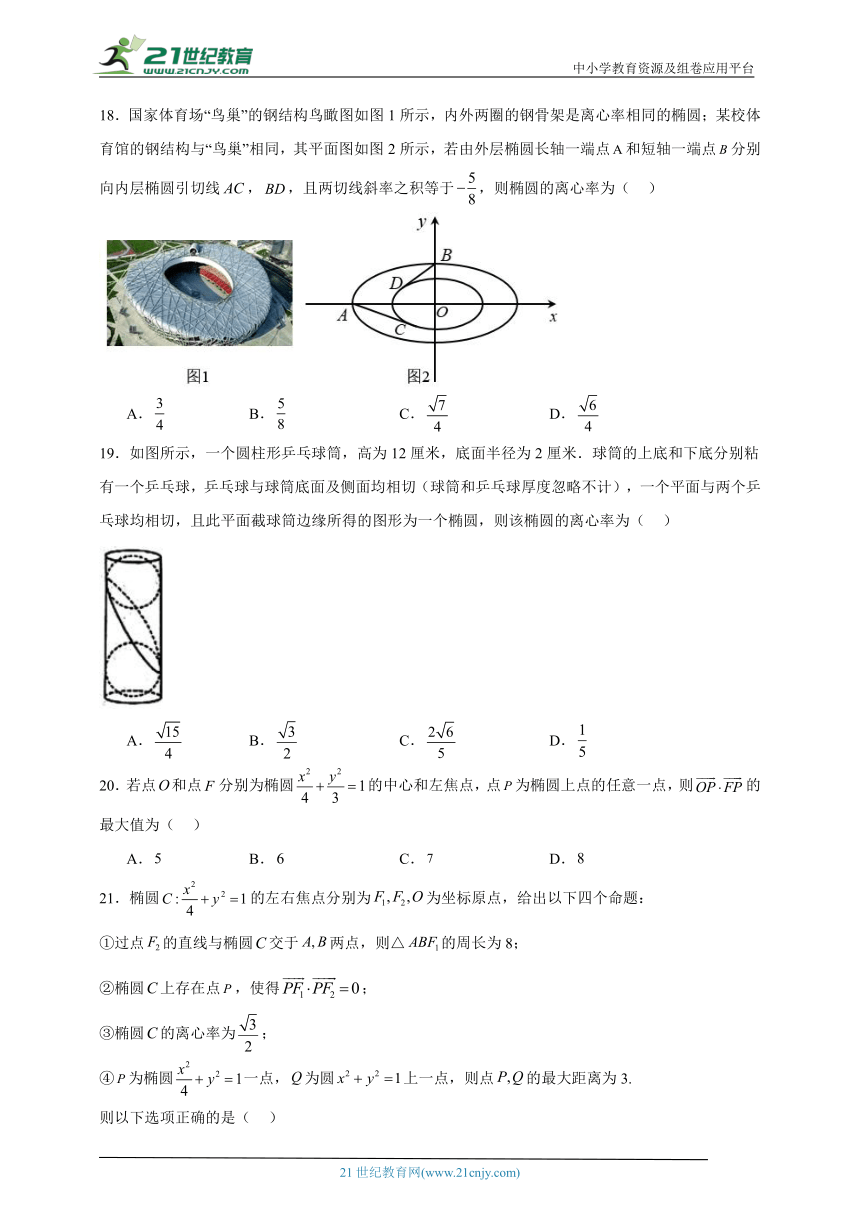
18.国家体育场“鸟巢”的钢结构鸟瞰图如图1所示,内外两圈的钢骨架是离心率相同的椭圆;某校体育馆的钢结构与“鸟巢”相同,其平面图如图2所示,若由外层椭圆长轴一端点和短轴一端点分别向内层椭圆引切线,,且两切线斜率之积等于,则椭圆的离心率为( )
A. B. C. D.
19.如图所示,一个圆柱形乒乓球筒,高为12厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
A. B. C. D.
20.若点和点分别为椭圆的中心和左焦点,点为椭圆上点的任意一点,则的最大值为( )
A. B. C. D.
21.椭圆的左右焦点分别为为坐标原点,给出以下四个命题:
①过点的直线与椭圆交于两点,则△的周长为8;
②椭圆上存在点,使得;
③椭圆的离心率为;
④为椭圆一点,为圆上一点,则点的最大距离为3.
则以下选项正确的是( )
A.①② B.①③ C.①②③④ D.①②④
22.“”是“椭圆的离心率为”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
23.如图是5号篮球在太阳光照射下的影子,已知篮球的直径为,现太阳光与地面的夹角为,则此椭圆形影子的离心率为( )
A. B. C. D.
24.已知是椭圆的右焦点,点在上,直线与轴交于点,点为C上的动点,则的最小值为( )
A. B. C. D.
25.已知椭圆上存在点,使得,其中,分别为椭圆的左、右焦点,则该椭圆的离心率的取值范围是( )
A. B. C. D.
26.下列关于曲线的结论正确的是( )
A.曲线是椭圆 B.y的取值范围是
C.关于直线对称 D.曲线所围成的封闭图形面积大于6
27.设椭圆的左、右焦点分别为,,点M,N在C上(M位于第一象限),且点M,N关于原点O对称,若,,则椭圆C的离心率为( )
A. B. C. D.
28.若椭圆上存在两点到点的距离相等,则椭圆的离心率的取值范围是( )
A. B. C. D.
29.已知点是椭圆:上异于顶点的动点,,分别为椭圆的左、右焦点,为坐标原点,为的中点,的平分线与直线交于点,则四边形的面积的最大值为( )
A.1 B.2 C.3 D.
二、多选题
30.已知椭圆中心在原点,焦点在坐标轴上,若椭圆的离心率为,且过点,则椭圆的标准方程为( )
A. B. C. D.
31.油纸伞是中国传统工艺品,至今已有1000多年的历史,为宣传和推广这一传统工艺,某市文化宫于春分时节开展油纸伞文化艺术节.活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞的伞沿是一个半径为1的圆,圆心到伞柄底端的距离为1,阳光照射油纸丛在地面上形成了一个椭圆形的影子(春分时,该市的阳光照射方向与地面的夹角为),若伞柄底端正好位于该椭圆的左焦点位置,则( )
A.该椭圆的离心率为 B.该椭圆的离心率为
C.该椭圆的焦距为 D.该椭圆的焦距为
32.已知椭圆C的两个焦点分别为,,离心率为,且点P是椭圆上任意一点,则下列结论正确的是( )
A.椭圆C的方程为
B.的最大值为
C.当时,
D.椭圆的形状比椭圆C的形状更接近于圆
33.据中国载人航天工程办公室消息,北京时间2021年11月8日1时16分,经过约6.5小时的出舱活动,神舟十三号航天员乘组密切协同,圆满完成出舱活动全部既定任务,航天员翟志刚,王亚平安全返回天和核心舱,出舱活动取得圆满成功.已知天和核心舱的运行轨道是以地球中心为一个焦点的椭圆,设其近地点距地面N千米,远地点距地面M千米,地球半径为R千米,则下列说法正确的是( )
A.椭圆的短轴长为千米 B.椭圆的短轴长为千米
C.椭圆的焦距为千米 D.椭圆的长轴长为千米
三、填空题
34.已知椭圆的一个顶点为,右焦点为F,直线BF与椭圆的另一个交点为M,且,则该椭圆的离心率是__________.
35.以椭圆的两个焦点和短轴的两个顶点为四个顶点的椭圆的标准方程为______.
36.若椭圆的焦距为6,则k的值为______.
37.若、是椭圆C:的两个焦点,过的直线l与椭圆C交于A、B两点,O为坐标原点,则下列说法中正确的是______.(填序号)
①椭圆C的离心率为; ②存在点A使得;
③若,则; ④面积的最大值为12.
四、解答题
38.求下列椭圆的长轴和短轴的长、离心率、焦点和顶点坐标:
(1);
(2).
39.某海面上有A,B两个观测点,点B在点A正东方向4 n mile处.经多年观察研究,发现某种鱼群(将鱼群视为点P)洄游的路线是以A,B为焦点的椭圆C.现有渔船发现该鱼群在与点A,点B距离之和为8 n mile处.在点A,B,P所在的平面内,以A,B所在的直线为轴,线段的垂直平分线为轴建立平面直角坐标系.
(1)求椭圆C的方程;
(2)某日,研究人员在A,B两点同时用声呐探测仪发出信号探测该鱼群(探测过程中,信号传播速度相同且鱼群移动的路程忽略不计),A,B两点收到鱼群的反射信号所用的时间之比为,试确定此时鱼群P的位置(即点P的坐标).
40.已知椭圆的焦距为,离心率为.
(1)求椭圆C的标准方程;
(2)若点,点B在椭圆C上,求线段长度的最大值.
41.已知地球绕太阳运行的轨道是一个椭圆,太阳在它的一个焦点上,长轴长约为,椭圆焦距与长轴长的比约为.求地球的轨道中心与太阳间的距离以及近日点和远日点到太阳的距离(地球与太阳的半径忽略不计,精确到).
42.圆锥曲线又称圆锥截痕、圆锥截面、二次曲线,约在公元前300年左右就已被命名和研究了,数学家欧几里得、阿基米德、阿波罗尼斯对圆锥曲线的贡献都很大,阿波罗尼斯著有《圆锥曲线论》,对圆锥曲线的性质做了系统性的研究,之所以称为圆锥曲线,是因为这些曲线是由一个平面截一个正圆锥面得到的,其实用一个平面去截圆柱的侧面也会得到一些曲线.如图,一个底面半径为2、高为12的圆柱内有两个半径为2的球,分别与圆柱的上下底面相切,一个平面夹在两球之间,且与两球分别切于点,,该平面与圆柱侧面的交线为椭圆,求这个椭圆的离心率.
43.已知椭圆C的离心率为,焦点、.
(1)求椭圆C的方程;
(2)已知、,是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求的取值范围.
44.求满足下列各条件的椭圆的标准方程:
(1)长轴是短轴的3倍且经过点;
(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为;
(3)经过点,两点;
(4)与椭圆有相同离心率,且经过点.
45.某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).
(1)若最大拱高为6米,则隧道设计的拱宽至少是多少米?(结果取整数)
(2)如何设计拱高和拱宽,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:,椭圆的面积公式为,其中,分别为椭圆的长半轴和短半轴长.
参考答案:
1.D
【分析】根据椭圆的方程求得的值,即可求得焦距的值,得到答案.
【详解】由椭圆,可得,则,
所以椭圆的焦距为.
故选:D.
2.A
【分析】根据椭圆中长轴长、短轴长和焦点坐标的定义可答案.
【详解】在椭圆中,
所以椭圆的长轴长为 、短轴长为,焦点坐标为
故选:A
3.B
【分析】椭圆上的点P满足,找到取等时点P位置即可求出最大值.
【详解】椭圆上的点P满足,
当点P为的延长线与C的交点时,
达到最大值,最大值为.
故选:B
4.A
【分析】根据椭圆的性质可得椭圆上的点到右焦点距离最小值为,即可求出,再根据,即可得解;
【详解】解:根据椭圆的性质,椭圆上的点到右焦点距离最小值为,
即 ,又,所以,
由,所以;
故选:A
5.B
【分析】分焦点在x轴和在y轴两种情况,分别得到a,b的表达式,进而求得c的表达式,然后根据离心率得到关于k的方程,求解即可.
【详解】解:因为椭圆的离心率为,
当时,椭圆焦点在轴上,可得:,解得,
当时,椭圆焦点在轴上,可得:,解得.
或.
故选:B.
6.C
【分析】由已知条件可得与的值,进而得的值,然后得标准方程.
【详解】由于2c=2,所以c=1,
又因为,故,
,所以椭圆的标准方程为:.
故选:C
7.B
【分析】对焦点所在位置进行分类讨论,利用、进行求解.
【详解】因为椭圆的焦距是2,所以,
当椭圆焦点在轴上,,所以,
当椭圆焦点在轴上,,所以,故A,C,D错误.
故选:B.
8.B
【分析】分别求出椭圆与椭圆的长轴长、短轴长、焦距、焦点坐标和离心率,由此能求出结果.
【详解】解:椭圆,可知,,,
长轴长是10,短轴长是6;焦距是8;焦点坐标是;离心率是:.
椭圆中,
,,,
长轴长是,短轴长是;焦距是8;焦点坐标是;离心率是.
椭圆与椭圆关系为有相等的焦距.
故选:B.
9.D
【分析】根据椭圆的标准方程,可得以及离心率的值,即可求解.
【详解】将椭圆方程整理得,
其焦点在轴上,,,则,所以.
将椭圆方程整理得,其焦点在轴上,,,
则,所以,
故选:D.
10.D
【分析】讨论焦点在轴和轴两种情况,根据已知计算即可得出结果.
【详解】当椭圆的焦点在x轴上,设椭圆的方程为,由离心率为,
∴
∵椭圆过点(2,0),∴,∴ ,∴ ,
∴椭圆标准方程为
当椭圆的焦点在y轴上,同理易得:
故选:D.
11.D
【分析】根据长轴长算出后,由离心率可得的值,从而可得椭圆的标准方程.
【详解】因为长轴长为,故长半轴长,因为,所以半焦距,
故,
又焦点在轴上,所以椭圆的标准方程为,
故选:D
12.B
【分析】根据离心率及,解得关于的等量关系式,即可得解.
【详解】解:因为离心率,解得,,
分别为C的左右顶点,则,
B为上顶点,所以.
所以,因为
所以,将代入,解得,
故椭圆的方程为.
故选:B.
13.D
【详解】当焦点在x轴时,
,
当焦点在y轴时,
所以实数的取值范围是.
故选:D.
14.C
【分析】分和,利用离心率的定义求解.
【详解】解:当,即时,则,解得;
当,即时,则,解得,
综上:的值为或,
故选:C
15.B
【分析】设,再根据直线的斜率之积为列式,结合椭圆的方程化简即可.
【详解】设且,则.
又,故,故,所以.
故选:B
16.B
【分析】求出椭圆的焦点坐标,求出所求椭圆的长半轴长,结合椭圆的焦点位置可得出所求椭圆的标准方程.
【详解】椭圆的标准方程为,该椭圆的焦点坐标为,
设所求椭圆的长半轴长为,则,
故所求椭圆的标准方程为.
故选:B.
17.A
【分析】分别计算出两个椭圆的离心率,然后比较,谁的离心率越大且越接近于1,谁就越扁.
【详解】在椭圆中,,,.
在椭圆中,,,.
, 椭圆的图形更为扁平一些.
故选:A.
18.D
【分析】设内层椭圆方程为,由题可知外层椭圆可设成 ,再根据直线与椭圆的位置关系可求出,即可利用求出离心率.
【详解】设内层椭圆方程为,因为内外椭圆离心率相同,
外层椭圆可设成 ,
设切线A C的方程为, 与联立得:
,由, 则,
同理可得,, 则,
因此.
故选:D.
19.B
【分析】作出这个组合体的轴截面,借助平面几何知识求得椭圆长轴即可得解.
【详解】作出这个组合体的轴截面,它是矩形MNPQ内两个与矩形三边都相切的圆O1和圆O2,如图,
矩形MNPQ是球筒轴截面,圆O1和圆O2是两个乒乓球的截面大圆,线段CD是与乒乓球相切的平面被轴截面所截图形,
线段CD是椭圆的长轴,点A是平面与乒乓球相切的切点,由对称性知线段CD与O1O2互相平分于点O,
过D作DB⊥O1O2于B,连O1A,则O1A⊥OD,O1A=DB,而,则,
所以,椭圆长半轴长,显然椭圆短轴长为球筒底面圆直径,短半轴长,
半焦距,椭圆离心率为.
故选:B
【点睛】关键点睛:涉及与旋转体有关的组合体,作出轴截面,借助平面几何知识解题是解决问题的关键.
20.B
【解析】设点,可得出,且有,利用平面向量的数量积的坐标运算结合二次函数的基本性质可求得的最大值.
【详解】由椭圆方程得,设,则,
为椭圆上一点,,可得,且有,
.
因为,当时,取得最大值.
故选:B.
【点睛】关键点点睛:本题考查椭圆中向量数量积最值的求解,解决本题的关键点在以下两方面:
(1)的变化是由点在椭圆上运动而产生,解题时可设,将利用点的坐标加以表示;
(2)在求的最值时,充分利用椭圆的有界性结合二次函数的基本性质求解.
21.C
【分析】根据椭圆方程写出a、b、c及焦点坐标,由椭圆定义求焦点三角形的周长判断①,根据椭圆的性质及余弦定理求的最大值,进而确定其范围判断②,直接法求离心率判断③,根据圆的方程确定与椭圆的位置关系,进而判断的距离范围,即可判断④.
【详解】由题设,椭圆参数为,且、,
①由椭圆定义知:,则△的周长为8,正确;
②当在y轴上时,,而,此时,易知为,故,存在点使得,正确;
③椭圆的离心率为,正确;
④由椭圆和圆的方程知:它们在y轴上的交点为椭圆上下顶点,而圆在x轴上的交点为,所以,故的最大距离为3,正确.
故选:C
22.A
【解析】椭圆离心率为,可得:时,,或时,,解得m即可判断出结论.
【详解】椭圆离心率为,可得:
时,,;
时,,
总之或.“”是“椭圆离心率为”的充分不必要条件.
故选:A.
【点睛】本题考查了椭圆的标准方程及其性质、充分不必要条件的判定方法,考查了推理能力与计算能力,属于基础题.
23.B
【分析】利用球的对称性,作出截面图,从而判断,
【详解】
如图, 是两条与球相切的直线,分别切于点A,C,
与底面交于点B,D,
,
过C作 交于E,C,则,
在 中,
, , , ,
,求出离心率.
那么椭圆中 , ,
.
故选:B
【点睛】需要准确得出截面图,理解椭圆的短轴长和篮球的直径是一样的,然后借助平面图形求解,对空间想象能力有一定的要求.
24.C
【分析】由题可得椭圆,进而可得,利用向量数量积的坐标表示可得,再结合条件及二次函数的性质即求.
【详解】由题可得,
∴,即椭圆,
∴,直线方程为,
∴,又,
设,则,,
∴
,又,
∴当时,有最小值为.
故选:C.
25.D
【分析】先由椭圆的定义结合已知求得,再由求得的不等关系,即可求得离心率的取值范围.
【详解】由椭圆的定义得,又∵,∴,,
而,当且仅当点在椭圆右顶点时等号成立,
即,即,则,即.
故选:D.
26.D
【分析】根据椭圆的标准方程即可判断A;易得,即可判断B;举出反例即可判断C;求出曲线与坐标轴的四个交点所构成的四边形的面积,即可判断D.
【详解】解:因为曲线,不是椭圆方程,
所以曲线不是椭圆,故A正确;
因为曲线,
所以,所以,故B错误;
曲线与轴正半轴的交点坐标为,
若曲线关于直线对称,
则点也在曲线上,
又,所以点不在曲线上,
所以曲线不关于直线对称,故C错误;
对于D,曲线与坐标轴的交点坐标为,
则以四点为顶点的四边形的面积为,
所以曲线所围成的封闭图形面积大于6,故D正确.
故选:D.
27.C
【分析】根据椭圆的定义及所给条件可得出,再由勾股定理可得,据此可求出离心率得解.
【详解】依题意作图,由于,并且线段MN,互相平分,
∴四边形是矩形,其中,,
设,则,
根据勾股定理,,,
整理得,
由于点M在第一象限,,
由,得,即,
整理得,即,解得.
故选:C.
28.B
【分析】利用点差法可得直线AB的斜率,从而可得AB垂直平分线直线方程,由点P在AB垂直平分线上,结合AB的中点在椭圆内可解.
【详解】记中点为,则,
由题意点在线段的中垂线上,
将坐标代入椭圆方程得
两式相减可得,
所以,得,
所以的中垂线的方程为,令得,
由题意,,故,所以
所以
故选:B.
29.B
【分析】由题,结合角平分线性质与椭圆的性质,,为到的距离,又是的中位线,故,结合余弦定理,设,即可表示出,即可讨论最值
【详解】
由图,,,故,,又平分,则到、的距离相等,设为,则
设,则,,由是的中位线,易得,即,由椭圆性质易知,存在点为椭圆上异于顶点的动点,使,此时最大,且为2
故选:B
30.AC
【分析】分焦点在轴上、焦点在轴上两种情况求解,分别设出椭圆的方程,然后由离心率和过点求解即可.
【详解】①当椭圆的焦点在轴上时,设椭圆的标准方程为,
由椭圆的离心率为,得,所以椭圆的方程为,
因为椭圆过点,所以,,,椭圆的标准方程为.
②当椭圆的焦点在轴上时,设椭圆方程为,
由椭圆的离心率为,得,所以椭圆的方程为,
因为椭圆过点,所以,,,椭圆的标准方程为.
故选:AC
31.BC
【分析】先求得,结合椭圆的知识以及正弦定理求得,进而求得椭圆的离心率和焦距.
【详解】,
如图,分别是椭圆的左 右顶点,是椭圆的左焦点,是圆的直径,为该圆的圆心.
因为,所以,
设椭圆的长轴长为,焦距为,则.
因为,
由正弦定理得,
解得,所以,
所以.
故选:BC
32.AC
【分析】根据离心率计算得到,,得到椭圆方程,计算的最大值,B错误,根据椭圆性质得到C正确,根据离心率的大小关系得到D错误,得到答案.
【详解】,,故,,故椭圆C的方程为,A正确;
的最大值为为,B错误;
,故当时,,C正确;
椭圆的离心率为,故椭圆C的形状更接近于圆,D错误.
故选:AC.
33.ACD
【分析】根据远地点以及近地点的距离,列出方程组,可求得,由此求得椭圆的短轴,长轴以及焦距,从而可判断每个选项的正误;
【详解】设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
则
解得 ,
所以,
故椭圆的短轴长为千米,A正确,B错误;
,故C正确,D正确,
故选:ACD.
34.
【分析】设出M的坐标,由得,从而得到,把点M的坐标代入椭圆的方程,求解即可.
【详解】设M的坐标为,由题知
,
,即,
把点M的坐标代入椭圆的方程得
,,.
故答案为:.
35.
【分析】求出椭圆的两个焦点和短轴的两个顶点,进而可以得出答案.
【详解】椭圆的两个焦点和短轴的两个顶点分别为,
则该椭圆的焦点在y轴上,设椭圆的标准方程为,
则
所以以此为四个顶点的椭圆的标准方程为,
故答案为:.
36.31或49/49或31
【分析】讨论椭圆焦点的位置,然后根据焦距,列等式求.
【详解】因为椭圆的焦距为6,所以c=3.
当椭圆的焦点在x轴上时,因为,,所以,解得k=31;
当椭圆的焦点在y轴上时,因为,,所以,解得k=49.
综上所述,k的值为31或49.
故答案为:31或49
37.②④
【分析】对于①,根据方程求出,再求离心率,对于②,设,表示出,然后求,判断方程是否有解即可,对于③,利用椭圆的定义求解,对于④,利用椭圆的性质求解.
【详解】对①,由题得a=5,b=3,c=4,离心率为,故①错误.
对②,设,得椭圆的参数方程为(t为参数),,,所以,.若存在点A使,则,即,得有解,故存在点A使,故②正确.
对③,因为,故③错误.
对④,当A位于短轴端点时,此时的面积最大,所以,故④正确.
故答案为:②④
38.(1)长轴长为6,短轴长为2,离心率为,焦点坐标为与,顶点坐标为,,,
(2)长轴长为,短轴长为4,离心率为,焦点坐标为,顶点坐标为.
【分析】把椭圆方程化为标准方程,结合的值求出长轴长,短轴长,离心率及焦点坐标,顶点坐标.
【详解】(1)整理为:,焦点在x轴上,则,,,所以长轴长为,短轴长为,离心率,焦点为与,顶点坐标为,,,
(2),整理为:,焦点在y轴上,则
,,所以,长轴长为,短轴长为,离心率,焦点为,顶点坐标为
39.(1)
(2)点的坐标为或
【分析】(1)首先椭圆的标准方程为,根据题意得到,,再计算的值即可得到答案.
(2)根据已知条件得到,,设,得到,再解方程组即可.
【详解】(1)设椭圆的标准方程为,
因为,,
所以,,,
于是椭圆的方程为.
(2)易知,.
因为,,
所以,.
设,则,解得
所以点的坐标为或.
40.(1)
(2)
【分析】(1)由题意可得,,求出,再由 求出,从而可求得椭圆方程,
(2)设,然后利用距离公式和二次函数的性质求解即可
【详解】(1)依题意,得,离心率,
所以,
所以椭圆C的标准方程为.
(2)设,则,则有
所以,
由两点间的距离公式,得
,
因为,
所以当时,线段的长度最大,为.
41.轨道中心与太阳间距离;近日点到太阳的距离;远日点到太阳的距离
【分析】由题意求出,再由椭圆的性质即可得出答案.
【详解】因为椭圆的长轴长为 ,所以 ,
又因为椭圆焦距与长轴长的比约为,所以,
则 ,
所以地球的轨道中心与太阳间的距离 ,
所以近日点到太阳的距离为 ,
所以远日点到太阳的距离为 .
故轨道中心与太阳间距离;近日点到太阳的距离;远日点到太阳的距离
42.
【分析】作出截面,根据平面与球相切的性质,结合直角三角形中各边的关系与勾股定理等,求解椭圆的基本量即可.
【详解】设椭圆的方程为.
作出几何体的轴截面图,如图所示,
点M,N是P圆柱内两个内切球的球心,,是椭圆的两个焦点,其中O是与的交点,.
根据圆的切线的性质,可得,,
由题意,可知,,
所以,
所以,即,
所以在中,,则,
所以,
所以,即a=4,
所以椭圆的离心率.
43.(1)
(2)
【分析】(1)根据已知条件求得,从而求得椭圆的方程.
(2)由,结合椭圆方程来求得的取值范围.
【详解】(1)依题意,,
所以椭圆的方程为.
(2)依题意,,
由于∠APB是钝角,所以①,
由于是椭圆C在第一象限部分上的一动点,
所以,且②,
将②代入①得,,则
所以的取值范围是.
44.(1)或
(2)或
(3)
(4)或
【分析】(1)分焦点在x轴、焦点在y轴上,设椭圆方程并代入点坐标可得答案;
(2)根据和可得答案;
(3)设方程为,代入坐标可得答案;
(4)椭圆的离心率是,所以,分焦点在x轴、焦点在y轴,利用和过点可得答案.
【详解】(1)若焦点在x轴上,设方程为,
∵椭圆过点,∴得,
∵,∴,∴方程为,
若焦点在y轴上,
设方程为,
∵椭圆过点,∴得,
又,∴,∴方程为.
综上所述,椭圆方程为或;
(2)由已知,有解得,,
若焦点在y轴上,则,
若焦点在x轴上,,
∴所求椭圆方程为或;
(3)设方程为,
则有,解得,
则所求椭圆方程为;
(4)椭圆的离心率是,所以,,
当焦点在x轴上时,
设所求椭圆的方程是,
∴,解得,
∴所求椭圆方程为;
当焦点在y轴上时,设所求椭圆的方程为,
∴,解得,
∴椭圆的标准方程为,
故所求椭圆标准方程为或.
45.(1)此隧道设计的拱宽至少是22米(2)当拱高为7米、拱宽为18米时,土方工程量最小
【分析】(1)建立直角坐标系,设椭圆方程为,根据对称性,将点代入椭圆方程,即可求解;
(2)由点在椭圆上或在椭圆内,得,利用基本不等式,即可求出椭圆的面积的最小值,根据体积公式,即可求解.
【详解】(1)建立直角坐标系如图所示,
则点在椭圆上,
将与点代入椭圆方程,得,
此时,
因此隧道设计的拱宽至少是22米.
(2)由椭圆方程,得,
因为,即,,
由于隧道长度为1.5千米,故隧道的土方工程量,
当取得最小值时,有且,得,,
此时,.
①若,此时,此时,
②若,此时,此时,
因为,故当拱高为7米、拱宽为18米时,土方工程量最小.
【点睛】本题考查椭圆的实际运用,考查椭圆的标准方程,并以椭圆为背景,考查利用利用基本不等式求值,属于较难题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【夯实基础】2023-2024高二数学同步限时训练(新人教A版2019)专题11 椭圆的简单几何性质
一、单选题
1.椭圆的焦距为( )
A. B. C. D.
2.椭圆的长轴长、短轴长和焦点坐标依次为( ).
A.,,B.,,C.,, D.,,
3.已知,分别为椭圆的两个焦点,P为椭圆上一点,则的最大值为( )
A.2 B. C.4 D.
4.已知椭圆C:上的动点P到右焦点距离的最小值为,则( )
A.1 B. C. D.
5.如果椭圆的离心率为,则( )
A. B.或 C. D.或
6.已知椭圆的焦距为2,离心率,则椭圆的标准方程为( )
A. B. C. D.
7.已知椭圆的焦距是2,则离心率e的值是( )
A. B.或 C.或 D.或
8.若椭圆与椭圆,则两椭圆必定( ).
A.有相等的长轴长 B.有相等的焦距
C.有相等的短轴长 D.长轴长与焦距之比相等
9.已知椭圆与,则两个椭圆( )
A.有相同的长轴与短轴 B.有相同的焦距
C.有相同的焦点 D.有相同的离心率
10.中心在原点,焦点在坐标轴上,离心率为,且过点的椭圆方程是( )
A. B.或
C. D.或
11.焦点在轴上,长轴长为10,离心率为的椭圆的标准方程为( )
A. B.
C. D.
12.已知椭圆的离心率为,分别为C的左、右顶点,B为C的上顶点.若,则C的方程为( )
A. B. C. D.
13.设是椭圆的离心率,且,则实数的取值范围是
A. B.
C. D.
14.若椭圆的离心率为,则的值为( )
A. B. C.或 D.或
15.椭圆的左顶点为,点均在上,且关于原点对称.若直线的斜率之积为,则的离心率为( )
A. B. C. D.
16.与椭圆有相同的焦点,且短半轴长为的椭圆方程是( )
A. B. C. D.
17.离心率和椭圆形状的有关,据此判断椭圆和,则和哪个图形更为扁平( )
A. B.
C.相同 D.无法判断
18.国家体育场“鸟巢”的钢结构鸟瞰图如图1所示,内外两圈的钢骨架是离心率相同的椭圆;某校体育馆的钢结构与“鸟巢”相同,其平面图如图2所示,若由外层椭圆长轴一端点和短轴一端点分别向内层椭圆引切线,,且两切线斜率之积等于,则椭圆的离心率为( )
A. B. C. D.
19.如图所示,一个圆柱形乒乓球筒,高为12厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
A. B. C. D.
20.若点和点分别为椭圆的中心和左焦点,点为椭圆上点的任意一点,则的最大值为( )
A. B. C. D.
21.椭圆的左右焦点分别为为坐标原点,给出以下四个命题:
①过点的直线与椭圆交于两点,则△的周长为8;
②椭圆上存在点,使得;
③椭圆的离心率为;
④为椭圆一点,为圆上一点,则点的最大距离为3.
则以下选项正确的是( )
A.①② B.①③ C.①②③④ D.①②④
22.“”是“椭圆的离心率为”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
23.如图是5号篮球在太阳光照射下的影子,已知篮球的直径为,现太阳光与地面的夹角为,则此椭圆形影子的离心率为( )
A. B. C. D.
24.已知是椭圆的右焦点,点在上,直线与轴交于点,点为C上的动点,则的最小值为( )
A. B. C. D.
25.已知椭圆上存在点,使得,其中,分别为椭圆的左、右焦点,则该椭圆的离心率的取值范围是( )
A. B. C. D.
26.下列关于曲线的结论正确的是( )
A.曲线是椭圆 B.y的取值范围是
C.关于直线对称 D.曲线所围成的封闭图形面积大于6
27.设椭圆的左、右焦点分别为,,点M,N在C上(M位于第一象限),且点M,N关于原点O对称,若,,则椭圆C的离心率为( )
A. B. C. D.
28.若椭圆上存在两点到点的距离相等,则椭圆的离心率的取值范围是( )
A. B. C. D.
29.已知点是椭圆:上异于顶点的动点,,分别为椭圆的左、右焦点,为坐标原点,为的中点,的平分线与直线交于点,则四边形的面积的最大值为( )
A.1 B.2 C.3 D.
二、多选题
30.已知椭圆中心在原点,焦点在坐标轴上,若椭圆的离心率为,且过点,则椭圆的标准方程为( )
A. B. C. D.
31.油纸伞是中国传统工艺品,至今已有1000多年的历史,为宣传和推广这一传统工艺,某市文化宫于春分时节开展油纸伞文化艺术节.活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞的伞沿是一个半径为1的圆,圆心到伞柄底端的距离为1,阳光照射油纸丛在地面上形成了一个椭圆形的影子(春分时,该市的阳光照射方向与地面的夹角为),若伞柄底端正好位于该椭圆的左焦点位置,则( )
A.该椭圆的离心率为 B.该椭圆的离心率为
C.该椭圆的焦距为 D.该椭圆的焦距为
32.已知椭圆C的两个焦点分别为,,离心率为,且点P是椭圆上任意一点,则下列结论正确的是( )
A.椭圆C的方程为
B.的最大值为
C.当时,
D.椭圆的形状比椭圆C的形状更接近于圆
33.据中国载人航天工程办公室消息,北京时间2021年11月8日1时16分,经过约6.5小时的出舱活动,神舟十三号航天员乘组密切协同,圆满完成出舱活动全部既定任务,航天员翟志刚,王亚平安全返回天和核心舱,出舱活动取得圆满成功.已知天和核心舱的运行轨道是以地球中心为一个焦点的椭圆,设其近地点距地面N千米,远地点距地面M千米,地球半径为R千米,则下列说法正确的是( )
A.椭圆的短轴长为千米 B.椭圆的短轴长为千米
C.椭圆的焦距为千米 D.椭圆的长轴长为千米
三、填空题
34.已知椭圆的一个顶点为,右焦点为F,直线BF与椭圆的另一个交点为M,且,则该椭圆的离心率是__________.
35.以椭圆的两个焦点和短轴的两个顶点为四个顶点的椭圆的标准方程为______.
36.若椭圆的焦距为6,则k的值为______.
37.若、是椭圆C:的两个焦点,过的直线l与椭圆C交于A、B两点,O为坐标原点,则下列说法中正确的是______.(填序号)
①椭圆C的离心率为; ②存在点A使得;
③若,则; ④面积的最大值为12.
四、解答题
38.求下列椭圆的长轴和短轴的长、离心率、焦点和顶点坐标:
(1);
(2).
39.某海面上有A,B两个观测点,点B在点A正东方向4 n mile处.经多年观察研究,发现某种鱼群(将鱼群视为点P)洄游的路线是以A,B为焦点的椭圆C.现有渔船发现该鱼群在与点A,点B距离之和为8 n mile处.在点A,B,P所在的平面内,以A,B所在的直线为轴,线段的垂直平分线为轴建立平面直角坐标系.
(1)求椭圆C的方程;
(2)某日,研究人员在A,B两点同时用声呐探测仪发出信号探测该鱼群(探测过程中,信号传播速度相同且鱼群移动的路程忽略不计),A,B两点收到鱼群的反射信号所用的时间之比为,试确定此时鱼群P的位置(即点P的坐标).
40.已知椭圆的焦距为,离心率为.
(1)求椭圆C的标准方程;
(2)若点,点B在椭圆C上,求线段长度的最大值.
41.已知地球绕太阳运行的轨道是一个椭圆,太阳在它的一个焦点上,长轴长约为,椭圆焦距与长轴长的比约为.求地球的轨道中心与太阳间的距离以及近日点和远日点到太阳的距离(地球与太阳的半径忽略不计,精确到).
42.圆锥曲线又称圆锥截痕、圆锥截面、二次曲线,约在公元前300年左右就已被命名和研究了,数学家欧几里得、阿基米德、阿波罗尼斯对圆锥曲线的贡献都很大,阿波罗尼斯著有《圆锥曲线论》,对圆锥曲线的性质做了系统性的研究,之所以称为圆锥曲线,是因为这些曲线是由一个平面截一个正圆锥面得到的,其实用一个平面去截圆柱的侧面也会得到一些曲线.如图,一个底面半径为2、高为12的圆柱内有两个半径为2的球,分别与圆柱的上下底面相切,一个平面夹在两球之间,且与两球分别切于点,,该平面与圆柱侧面的交线为椭圆,求这个椭圆的离心率.
43.已知椭圆C的离心率为,焦点、.
(1)求椭圆C的方程;
(2)已知、,是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求的取值范围.
44.求满足下列各条件的椭圆的标准方程:
(1)长轴是短轴的3倍且经过点;
(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为;
(3)经过点,两点;
(4)与椭圆有相同离心率,且经过点.
45.某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).
(1)若最大拱高为6米,则隧道设计的拱宽至少是多少米?(结果取整数)
(2)如何设计拱高和拱宽,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:,椭圆的面积公式为,其中,分别为椭圆的长半轴和短半轴长.
参考答案:
1.D
【分析】根据椭圆的方程求得的值,即可求得焦距的值,得到答案.
【详解】由椭圆,可得,则,
所以椭圆的焦距为.
故选:D.
2.A
【分析】根据椭圆中长轴长、短轴长和焦点坐标的定义可答案.
【详解】在椭圆中,
所以椭圆的长轴长为 、短轴长为,焦点坐标为
故选:A
3.B
【分析】椭圆上的点P满足,找到取等时点P位置即可求出最大值.
【详解】椭圆上的点P满足,
当点P为的延长线与C的交点时,
达到最大值,最大值为.
故选:B
4.A
【分析】根据椭圆的性质可得椭圆上的点到右焦点距离最小值为,即可求出,再根据,即可得解;
【详解】解:根据椭圆的性质,椭圆上的点到右焦点距离最小值为,
即 ,又,所以,
由,所以;
故选:A
5.B
【分析】分焦点在x轴和在y轴两种情况,分别得到a,b的表达式,进而求得c的表达式,然后根据离心率得到关于k的方程,求解即可.
【详解】解:因为椭圆的离心率为,
当时,椭圆焦点在轴上,可得:,解得,
当时,椭圆焦点在轴上,可得:,解得.
或.
故选:B.
6.C
【分析】由已知条件可得与的值,进而得的值,然后得标准方程.
【详解】由于2c=2,所以c=1,
又因为,故,
,所以椭圆的标准方程为:.
故选:C
7.B
【分析】对焦点所在位置进行分类讨论,利用、进行求解.
【详解】因为椭圆的焦距是2,所以,
当椭圆焦点在轴上,,所以,
当椭圆焦点在轴上,,所以,故A,C,D错误.
故选:B.
8.B
【分析】分别求出椭圆与椭圆的长轴长、短轴长、焦距、焦点坐标和离心率,由此能求出结果.
【详解】解:椭圆,可知,,,
长轴长是10,短轴长是6;焦距是8;焦点坐标是;离心率是:.
椭圆中,
,,,
长轴长是,短轴长是;焦距是8;焦点坐标是;离心率是.
椭圆与椭圆关系为有相等的焦距.
故选:B.
9.D
【分析】根据椭圆的标准方程,可得以及离心率的值,即可求解.
【详解】将椭圆方程整理得,
其焦点在轴上,,,则,所以.
将椭圆方程整理得,其焦点在轴上,,,
则,所以,
故选:D.
10.D
【分析】讨论焦点在轴和轴两种情况,根据已知计算即可得出结果.
【详解】当椭圆的焦点在x轴上,设椭圆的方程为,由离心率为,
∴
∵椭圆过点(2,0),∴,∴ ,∴ ,
∴椭圆标准方程为
当椭圆的焦点在y轴上,同理易得:
故选:D.
11.D
【分析】根据长轴长算出后,由离心率可得的值,从而可得椭圆的标准方程.
【详解】因为长轴长为,故长半轴长,因为,所以半焦距,
故,
又焦点在轴上,所以椭圆的标准方程为,
故选:D
12.B
【分析】根据离心率及,解得关于的等量关系式,即可得解.
【详解】解:因为离心率,解得,,
分别为C的左右顶点,则,
B为上顶点,所以.
所以,因为
所以,将代入,解得,
故椭圆的方程为.
故选:B.
13.D
【详解】当焦点在x轴时,
,
当焦点在y轴时,
所以实数的取值范围是.
故选:D.
14.C
【分析】分和,利用离心率的定义求解.
【详解】解:当,即时,则,解得;
当,即时,则,解得,
综上:的值为或,
故选:C
15.B
【分析】设,再根据直线的斜率之积为列式,结合椭圆的方程化简即可.
【详解】设且,则.
又,故,故,所以.
故选:B
16.B
【分析】求出椭圆的焦点坐标,求出所求椭圆的长半轴长,结合椭圆的焦点位置可得出所求椭圆的标准方程.
【详解】椭圆的标准方程为,该椭圆的焦点坐标为,
设所求椭圆的长半轴长为,则,
故所求椭圆的标准方程为.
故选:B.
17.A
【分析】分别计算出两个椭圆的离心率,然后比较,谁的离心率越大且越接近于1,谁就越扁.
【详解】在椭圆中,,,.
在椭圆中,,,.
, 椭圆的图形更为扁平一些.
故选:A.
18.D
【分析】设内层椭圆方程为,由题可知外层椭圆可设成 ,再根据直线与椭圆的位置关系可求出,即可利用求出离心率.
【详解】设内层椭圆方程为,因为内外椭圆离心率相同,
外层椭圆可设成 ,
设切线A C的方程为, 与联立得:
,由, 则,
同理可得,, 则,
因此.
故选:D.
19.B
【分析】作出这个组合体的轴截面,借助平面几何知识求得椭圆长轴即可得解.
【详解】作出这个组合体的轴截面,它是矩形MNPQ内两个与矩形三边都相切的圆O1和圆O2,如图,
矩形MNPQ是球筒轴截面,圆O1和圆O2是两个乒乓球的截面大圆,线段CD是与乒乓球相切的平面被轴截面所截图形,
线段CD是椭圆的长轴,点A是平面与乒乓球相切的切点,由对称性知线段CD与O1O2互相平分于点O,
过D作DB⊥O1O2于B,连O1A,则O1A⊥OD,O1A=DB,而,则,
所以,椭圆长半轴长,显然椭圆短轴长为球筒底面圆直径,短半轴长,
半焦距,椭圆离心率为.
故选:B
【点睛】关键点睛:涉及与旋转体有关的组合体,作出轴截面,借助平面几何知识解题是解决问题的关键.
20.B
【解析】设点,可得出,且有,利用平面向量的数量积的坐标运算结合二次函数的基本性质可求得的最大值.
【详解】由椭圆方程得,设,则,
为椭圆上一点,,可得,且有,
.
因为,当时,取得最大值.
故选:B.
【点睛】关键点点睛:本题考查椭圆中向量数量积最值的求解,解决本题的关键点在以下两方面:
(1)的变化是由点在椭圆上运动而产生,解题时可设,将利用点的坐标加以表示;
(2)在求的最值时,充分利用椭圆的有界性结合二次函数的基本性质求解.
21.C
【分析】根据椭圆方程写出a、b、c及焦点坐标,由椭圆定义求焦点三角形的周长判断①,根据椭圆的性质及余弦定理求的最大值,进而确定其范围判断②,直接法求离心率判断③,根据圆的方程确定与椭圆的位置关系,进而判断的距离范围,即可判断④.
【详解】由题设,椭圆参数为,且、,
①由椭圆定义知:,则△的周长为8,正确;
②当在y轴上时,,而,此时,易知为,故,存在点使得,正确;
③椭圆的离心率为,正确;
④由椭圆和圆的方程知:它们在y轴上的交点为椭圆上下顶点,而圆在x轴上的交点为,所以,故的最大距离为3,正确.
故选:C
22.A
【解析】椭圆离心率为,可得:时,,或时,,解得m即可判断出结论.
【详解】椭圆离心率为,可得:
时,,;
时,,
总之或.“”是“椭圆离心率为”的充分不必要条件.
故选:A.
【点睛】本题考查了椭圆的标准方程及其性质、充分不必要条件的判定方法,考查了推理能力与计算能力,属于基础题.
23.B
【分析】利用球的对称性,作出截面图,从而判断,
【详解】
如图, 是两条与球相切的直线,分别切于点A,C,
与底面交于点B,D,
,
过C作 交于E,C,则,
在 中,
, , , ,
,求出离心率.
那么椭圆中 , ,
.
故选:B
【点睛】需要准确得出截面图,理解椭圆的短轴长和篮球的直径是一样的,然后借助平面图形求解,对空间想象能力有一定的要求.
24.C
【分析】由题可得椭圆,进而可得,利用向量数量积的坐标表示可得,再结合条件及二次函数的性质即求.
【详解】由题可得,
∴,即椭圆,
∴,直线方程为,
∴,又,
设,则,,
∴
,又,
∴当时,有最小值为.
故选:C.
25.D
【分析】先由椭圆的定义结合已知求得,再由求得的不等关系,即可求得离心率的取值范围.
【详解】由椭圆的定义得,又∵,∴,,
而,当且仅当点在椭圆右顶点时等号成立,
即,即,则,即.
故选:D.
26.D
【分析】根据椭圆的标准方程即可判断A;易得,即可判断B;举出反例即可判断C;求出曲线与坐标轴的四个交点所构成的四边形的面积,即可判断D.
【详解】解:因为曲线,不是椭圆方程,
所以曲线不是椭圆,故A正确;
因为曲线,
所以,所以,故B错误;
曲线与轴正半轴的交点坐标为,
若曲线关于直线对称,
则点也在曲线上,
又,所以点不在曲线上,
所以曲线不关于直线对称,故C错误;
对于D,曲线与坐标轴的交点坐标为,
则以四点为顶点的四边形的面积为,
所以曲线所围成的封闭图形面积大于6,故D正确.
故选:D.
27.C
【分析】根据椭圆的定义及所给条件可得出,再由勾股定理可得,据此可求出离心率得解.
【详解】依题意作图,由于,并且线段MN,互相平分,
∴四边形是矩形,其中,,
设,则,
根据勾股定理,,,
整理得,
由于点M在第一象限,,
由,得,即,
整理得,即,解得.
故选:C.
28.B
【分析】利用点差法可得直线AB的斜率,从而可得AB垂直平分线直线方程,由点P在AB垂直平分线上,结合AB的中点在椭圆内可解.
【详解】记中点为,则,
由题意点在线段的中垂线上,
将坐标代入椭圆方程得
两式相减可得,
所以,得,
所以的中垂线的方程为,令得,
由题意,,故,所以
所以
故选:B.
29.B
【分析】由题,结合角平分线性质与椭圆的性质,,为到的距离,又是的中位线,故,结合余弦定理,设,即可表示出,即可讨论最值
【详解】
由图,,,故,,又平分,则到、的距离相等,设为,则
设,则,,由是的中位线,易得,即,由椭圆性质易知,存在点为椭圆上异于顶点的动点,使,此时最大,且为2
故选:B
30.AC
【分析】分焦点在轴上、焦点在轴上两种情况求解,分别设出椭圆的方程,然后由离心率和过点求解即可.
【详解】①当椭圆的焦点在轴上时,设椭圆的标准方程为,
由椭圆的离心率为,得,所以椭圆的方程为,
因为椭圆过点,所以,,,椭圆的标准方程为.
②当椭圆的焦点在轴上时,设椭圆方程为,
由椭圆的离心率为,得,所以椭圆的方程为,
因为椭圆过点,所以,,,椭圆的标准方程为.
故选:AC
31.BC
【分析】先求得,结合椭圆的知识以及正弦定理求得,进而求得椭圆的离心率和焦距.
【详解】,
如图,分别是椭圆的左 右顶点,是椭圆的左焦点,是圆的直径,为该圆的圆心.
因为,所以,
设椭圆的长轴长为,焦距为,则.
因为,
由正弦定理得,
解得,所以,
所以.
故选:BC
32.AC
【分析】根据离心率计算得到,,得到椭圆方程,计算的最大值,B错误,根据椭圆性质得到C正确,根据离心率的大小关系得到D错误,得到答案.
【详解】,,故,,故椭圆C的方程为,A正确;
的最大值为为,B错误;
,故当时,,C正确;
椭圆的离心率为,故椭圆C的形状更接近于圆,D错误.
故选:AC.
33.ACD
【分析】根据远地点以及近地点的距离,列出方程组,可求得,由此求得椭圆的短轴,长轴以及焦距,从而可判断每个选项的正误;
【详解】设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
则
解得 ,
所以,
故椭圆的短轴长为千米,A正确,B错误;
,故C正确,D正确,
故选:ACD.
34.
【分析】设出M的坐标,由得,从而得到,把点M的坐标代入椭圆的方程,求解即可.
【详解】设M的坐标为,由题知
,
,即,
把点M的坐标代入椭圆的方程得
,,.
故答案为:.
35.
【分析】求出椭圆的两个焦点和短轴的两个顶点,进而可以得出答案.
【详解】椭圆的两个焦点和短轴的两个顶点分别为,
则该椭圆的焦点在y轴上,设椭圆的标准方程为,
则
所以以此为四个顶点的椭圆的标准方程为,
故答案为:.
36.31或49/49或31
【分析】讨论椭圆焦点的位置,然后根据焦距,列等式求.
【详解】因为椭圆的焦距为6,所以c=3.
当椭圆的焦点在x轴上时,因为,,所以,解得k=31;
当椭圆的焦点在y轴上时,因为,,所以,解得k=49.
综上所述,k的值为31或49.
故答案为:31或49
37.②④
【分析】对于①,根据方程求出,再求离心率,对于②,设,表示出,然后求,判断方程是否有解即可,对于③,利用椭圆的定义求解,对于④,利用椭圆的性质求解.
【详解】对①,由题得a=5,b=3,c=4,离心率为,故①错误.
对②,设,得椭圆的参数方程为(t为参数),,,所以,.若存在点A使,则,即,得有解,故存在点A使,故②正确.
对③,因为,故③错误.
对④,当A位于短轴端点时,此时的面积最大,所以,故④正确.
故答案为:②④
38.(1)长轴长为6,短轴长为2,离心率为,焦点坐标为与,顶点坐标为,,,
(2)长轴长为,短轴长为4,离心率为,焦点坐标为,顶点坐标为.
【分析】把椭圆方程化为标准方程,结合的值求出长轴长,短轴长,离心率及焦点坐标,顶点坐标.
【详解】(1)整理为:,焦点在x轴上,则,,,所以长轴长为,短轴长为,离心率,焦点为与,顶点坐标为,,,
(2),整理为:,焦点在y轴上,则
,,所以,长轴长为,短轴长为,离心率,焦点为,顶点坐标为
39.(1)
(2)点的坐标为或
【分析】(1)首先椭圆的标准方程为,根据题意得到,,再计算的值即可得到答案.
(2)根据已知条件得到,,设,得到,再解方程组即可.
【详解】(1)设椭圆的标准方程为,
因为,,
所以,,,
于是椭圆的方程为.
(2)易知,.
因为,,
所以,.
设,则,解得
所以点的坐标为或.
40.(1)
(2)
【分析】(1)由题意可得,,求出,再由 求出,从而可求得椭圆方程,
(2)设,然后利用距离公式和二次函数的性质求解即可
【详解】(1)依题意,得,离心率,
所以,
所以椭圆C的标准方程为.
(2)设,则,则有
所以,
由两点间的距离公式,得
,
因为,
所以当时,线段的长度最大,为.
41.轨道中心与太阳间距离;近日点到太阳的距离;远日点到太阳的距离
【分析】由题意求出,再由椭圆的性质即可得出答案.
【详解】因为椭圆的长轴长为 ,所以 ,
又因为椭圆焦距与长轴长的比约为,所以,
则 ,
所以地球的轨道中心与太阳间的距离 ,
所以近日点到太阳的距离为 ,
所以远日点到太阳的距离为 .
故轨道中心与太阳间距离;近日点到太阳的距离;远日点到太阳的距离
42.
【分析】作出截面,根据平面与球相切的性质,结合直角三角形中各边的关系与勾股定理等,求解椭圆的基本量即可.
【详解】设椭圆的方程为.
作出几何体的轴截面图,如图所示,
点M,N是P圆柱内两个内切球的球心,,是椭圆的两个焦点,其中O是与的交点,.
根据圆的切线的性质,可得,,
由题意,可知,,
所以,
所以,即,
所以在中,,则,
所以,
所以,即a=4,
所以椭圆的离心率.
43.(1)
(2)
【分析】(1)根据已知条件求得,从而求得椭圆的方程.
(2)由,结合椭圆方程来求得的取值范围.
【详解】(1)依题意,,
所以椭圆的方程为.
(2)依题意,,
由于∠APB是钝角,所以①,
由于是椭圆C在第一象限部分上的一动点,
所以,且②,
将②代入①得,,则
所以的取值范围是.
44.(1)或
(2)或
(3)
(4)或
【分析】(1)分焦点在x轴、焦点在y轴上,设椭圆方程并代入点坐标可得答案;
(2)根据和可得答案;
(3)设方程为,代入坐标可得答案;
(4)椭圆的离心率是,所以,分焦点在x轴、焦点在y轴,利用和过点可得答案.
【详解】(1)若焦点在x轴上,设方程为,
∵椭圆过点,∴得,
∵,∴,∴方程为,
若焦点在y轴上,
设方程为,
∵椭圆过点,∴得,
又,∴,∴方程为.
综上所述,椭圆方程为或;
(2)由已知,有解得,,
若焦点在y轴上,则,
若焦点在x轴上,,
∴所求椭圆方程为或;
(3)设方程为,
则有,解得,
则所求椭圆方程为;
(4)椭圆的离心率是,所以,,
当焦点在x轴上时,
设所求椭圆的方程是,
∴,解得,
∴所求椭圆方程为;
当焦点在y轴上时,设所求椭圆的方程为,
∴,解得,
∴椭圆的标准方程为,
故所求椭圆标准方程为或.
45.(1)此隧道设计的拱宽至少是22米(2)当拱高为7米、拱宽为18米时,土方工程量最小
【分析】(1)建立直角坐标系,设椭圆方程为,根据对称性,将点代入椭圆方程,即可求解;
(2)由点在椭圆上或在椭圆内,得,利用基本不等式,即可求出椭圆的面积的最小值,根据体积公式,即可求解.
【详解】(1)建立直角坐标系如图所示,
则点在椭圆上,
将与点代入椭圆方程,得,
此时,
因此隧道设计的拱宽至少是22米.
(2)由椭圆方程,得,
因为,即,,
由于隧道长度为1.5千米,故隧道的土方工程量,
当取得最小值时,有且,得,,
此时,.
①若,此时,此时,
②若,此时,此时,
因为,故当拱高为7米、拱宽为18米时,土方工程量最小.
【点睛】本题考查椭圆的实际运用,考查椭圆的标准方程,并以椭圆为背景,考查利用利用基本不等式求值,属于较难题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
