2022-2023学年山东省济南市钢城区八年级(下)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2022-2023学年山东省济南市钢城区八年级(下)期末数学试卷(五四学制)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 441.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-12 00:00:00 | ||
图片预览




文档简介
2022-2023学年山东省济南市钢城区八年级(下)期末数学试卷(五四学制)
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 化简的结果是( )
A. B. C. D.
2. 图是伸缩折叠不锈钢晾衣架的实物图,图是它的侧面示意图,与相交于点,,根据图中的数据可得的值为( )
A. B. C. D.
3. 下列计算中,正确的是( )
A. B.
C. D.
4. 如图,∽,,::,则为( )
A.
B.
C.
D.
5. 一元二次方程 的根的情况为( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
6. 某商店将一批夏装降价处理,经过两次降价后,由每件元降至元,求平均每次降价的百分率设平均每次降价的百分率为,可列方程( )
A. B.
C. D.
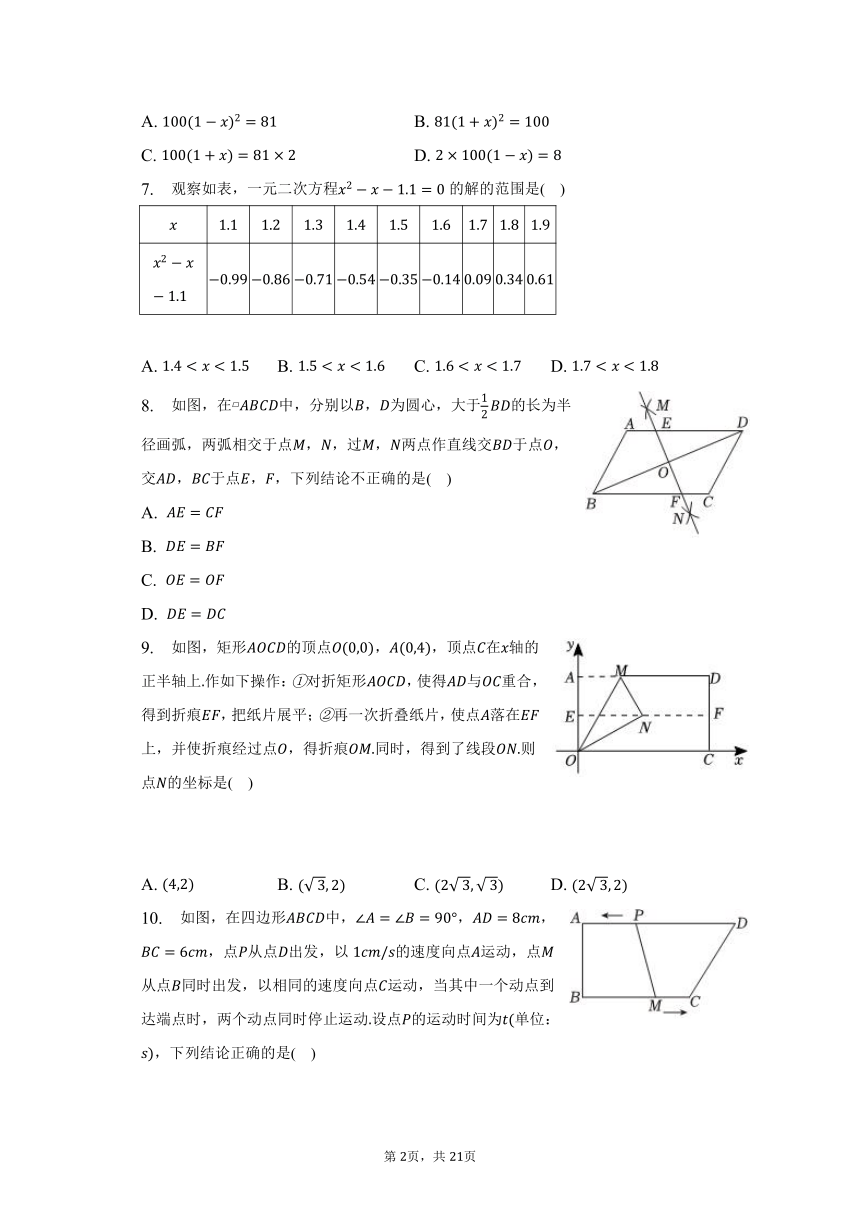
7. 观察如表,一元二次方程的解的范围是( )
A. B. C. D.
8. 如图,在 中,分别以,为圆心,大于的长为半径画弧,两弧相交于点,,过,两点作直线交于点,交,于点,,下列结论不正确的是( )
A.
B.
C.
D.
9. 如图,矩形的顶点,,顶点在轴的正半轴上作如下操作:对折矩形,使得与重合,得到折痕,把纸片展平;再一次折叠纸片,使点落在上,并使折痕经过点,得折痕同时,得到了线段则点的坐标是( )
A. B. C. D.
10. 如图,在四边形中,,,,点从点出发,以的速度向点运动,点从点同时出发,以相同的速度向点运动,当其中一个动点到达端点时,两个动点同时停止运动设点的运动时间为单位:,下列结论正确的是( )
A. 当时,四边形为矩形
B. 当时,四边形为平行四边形
C. 当时,
D. 当时,或
二、填空题(本大题共6小题,共24.0分)
11. 若,则:______.
12. 若代数式有意义,则的取值范围是______.
13. 若最简根式与是同类二次根式,则 ______ .
14. 若、是方程的两个实数根,则代数式的值为______ .
15. 如图,乐器上的一根弦,两个端点,固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,,之间的距离为______ .
16. 如图,菱形的对角线,相交于点,点为边上一动点不与点,重合,于点,于点,若,,则的最小值为 .
三、解答题(本大题共10小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:.
18. 本小题分
解方程:.
19. 本小题分
如图,在矩形中,点,在对角线上,且,连接,.
求证:.
20. 本小题分
在平面直角坐标系内,的位置如图所示.
将绕点顺时针旋转得到,作出.
以原点为位似中心,在第四象限内作出的位似图形,且与的相似比为:.
21. 本小题分
如图,已知等腰,,点、分别在、上,且.
求证:∽;
如果,,,求的长.
22. 本小题分
一款服装每件进价为元,销售价为元时,每天可售出件经市场调查发现,如果每件服装降价元,那么平均每天可多售出件.
设每件服装降价元,则每天销售量增加______ 件,每件服装盈利______ 元用含的代数式表示;
在让利于顾客的情况下,每件服装降价多少元时,商家平均每天能盈利元?
23. 本小题分
如图,已知和,,,点在边上,,边与相交于点.
求证:∽;
如果,,连结.
求证:四边形是菱形.
24. 本小题分
在解决问题“已知,求的值”时,小明是这样分析与解答的:
因为
所以,所以,
所以,所以.
请你根据小明的分析过程,解决如下问题:
化简:;
若,求的值.
25. 本小题分
如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
填空: ______ , ______ ;用含的代数式表示
当为几秒时,的长度等于.
是否存在某一时刻,使四边形的面积等于面积的?如果存在,求出的值,如果不存在,请说明理由,
26. 本小题分
原题再现:小百合特别喜欢探究数学问题,一天万老师给她这样一个几何问题:
和都是等边三角形,将绕着点旋转到图位置,求证:小百合很快就通过≌,论证了.
请你帮助小百合写出证明过程;
迁移应用:小百合想,把等边和等边都换成等腰直角三角形,将绕着点旋转到图位置,其中,那么和有什么数量关系呢?
请你帮助小百合写出结论,并给出证明;
如图,如果把等腰直角三角形换成正方形,将正方形绕点旋转,若,,在旋转过程中,当,,三点共线时,请直接写出的长度.
答案和解析
1.【答案】
【解析】解:,
故选:.
根据二次根式的性质求出即可.
本题考查了二次根式的性质的应用,主要考查学生的计算能力,题目比较好,难度不大.
2.【答案】
【解析】解:,
∽,
,
,
,
故选:.
由,可得出∽,进而得出,解出即可得出结论.
本题主要考查了三角形相似的判定和性质,熟练掌握相似的判定和性质是解此题的关键.
3.【答案】
【解析】解:.,故计算错误,不符合题意;
B.,故计算错误,不符合题意;
C.,故计算错误,符合题意;
D.,故计算错误,不符合题意;
故选:.
根据算术平方根的含义可判断;
根据二次根式的除法运算可判断;
根据二次根式的乘法运算可判断;
根据二次根式的减法运算可判断.
本题考查了算术平方根的含义,二次根式的加减乘除运算,掌握相应的运算法则是解本题的关键.
4.【答案】
【解析】解:::,
::,
相似比为:,即,,
;
故选:.
根据:的比,可得:的比,利用面积比是相似比的平方,可得,从而可得答案.
本题考查了形似三角形的性质,解题的关键是掌握面积比是相似比的平方.
5.【答案】
【解析】解:,
,
一元二次方程没有实数根,
故选D.
本题考查根的判别式,解题的关键是由根的判别式的正负判断一元二次方程根的情况.
6.【答案】
【解析】解:设平均每次降价的百分率为,根据题意列方程得:
,
故选:.
此题可设平均每次降价的百分率为,那么第一次降价后的单价是原来的,那么第二次降价后的单价是原来的,根据题意列方程解答即可.
本题考查的是平均变化率问题.解决这类问题所用的等量关系一般是:.
7.【答案】
【解析】
【分析】
本题考查了估算一元二次方程的近似解:用列举法估算一元二次方程的近似解,具体方法是:给出一些未知数的值,计算方程两边结果,当两边结果愈接近时,说明未知数的值愈接近方程的根.会估算一元二次方程的近似解是解题的关键.
根据图表数据找出一元二次方程等于时,未知数的值的范围,即可得到答案.
【解答】
解:时,,时,,
一元二次方程的解的范围是,
故选:.
8.【答案】
【解析】解:根据作图可知:垂直平分,
,
四边形是平行四边形,
,,
,
,
≌,
,,故B,C正确;
无法证明,故D错误;
故选:.
根据作图可知:垂直平分,根据线段垂直平分线的性质得到,根据平行四边形的性质得到,,根据全等三角形的性质得到,,故B,C正确;无法证明,故D错误.
本题考查了作图基本作图,垂直平分线的性质,尺规作图,菱形的判定与性质,全等三角形的判定与性质以及勾股定理等知识,掌握菱形的判定与性质是解答本题的关键.
9.【答案】
【解析】解:,,
,
四边形为矩形,,
,
根据折叠的性质可得,,,,
,
如图,过点作于点,
则四边形为矩形,
,,
在中,,
点的坐标为.
故选:.
根据题意可得,由折叠可知,,,得到,过点作于点,,,再根据勾股定理求得,以此即可得到点的坐标.
本题主要考查坐标与图形、折叠的性质、矩形的性质、勾股定理,熟练掌握折叠的性质是解题关键.
10.【答案】
【解析】解:根据题意,可得,,
,,
,,
当四边形为矩形时,,
即,
解得,
故A选项不符合题意;
当四边形为平行四边形,,
即,
解得,
故B选项不符合题意;
当时,分两种情况:
四边形是平行四边形,
此时,
即,
解得,
四边形是等腰梯形,
过点作于点,过点作于点,如图所示:
则,
,,
≌,
,
,
又,
,
解得,
综上,当时,或,
故C选项不符合题意,选项符合题意,
故选:.
根据题意,表示出,,和的长,当四边形为矩形时,根据,列方程求解即可;当四边形为平行四边形,根据,列方程求解即可;当时,分两种情况:四边形是平行四边形,四边形是等腰梯形,分别列方程求解即可.
本题考查了矩形的判定,平行四边形的判定,全等三角形的判定和性质,涉及动点问题,用含的代数式表示出各线段的长是解题的关键.
11.【答案】:
【解析】解:::,
故答案为::.
根据等式的性质,可得答案.
本题考查了比例的性质,利用等式的性质是解题关键.
12.【答案】
【解析】解:代数式有意义,
,
解得:,
故答案为:.
根据有意义得出,再求出答案即可.
本题考查了二次根式有意义的条件,能根据有意义得出是解此题的关键.
13.【答案】
【解析】解:最简根式与是同类二次根式,
,
,
,
故答案为:.
根据同类二次根式的定义可得,然后进行计算即可解答.
本题考查了同类二次根式,最简二次根式,熟练掌握同类二次根式的定义是解题的关键.
14.【答案】
【解析】解:是方程的实数根,
,
,
,
、是方程的两个实数根,
,
.
故答案为:.
先根据一元二次方程根的定义得到,则化为,再利用根与系数的关系得,然后利用整体代入的方法计算.
本题考查了根与系数的关系:若,是一元二次方程的两根时,,也考查了一元二次方程的解.
15.【答案】
【解析】解:弦,点是靠近点的黄金分割点,设,则,
,解方程得,,
点是靠近点的黄金分割点,设,则,
,解方程得,,
,之间的距离为,
故答案为:.
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比.其比值是一个无理数,用分数表示为,由此即可求解.
本题主要考查线段成比例,掌握线段成比例,黄金分割点的定义是解题的关键.
16.【答案】
【解析】解:连接,
四边形是菱形,
,,,
,
于点,于点,
,
四边形是矩形,
,
当取最小值时,的值最小,
当时,最小,
,
,
的最小值为,
故答案为:.
连接,根据菱形的性质得到,,,根据勾股定理得到,根据矩形的性质得到,根据三角形的面积公式即可得到结论.
本题考查了矩形的判定和性质,垂线段最短,菱形的性质,熟练掌握垂线段最短是解题的关键.
17.【答案】解:原式
.
【解析】直接利用二次根式的性质以及绝对值的性质、负整数指数幂的性质分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
18.【答案】解:移项得,
配方得,
即,
开方得,
,.
【解析】本题考查配方法解一元二次方程.
根据配方法即可解.
19.【答案】证明:四边形是矩形,
,.
.
,
,即.
在和中,,
≌,
.
【解析】证明≌,即可得出.
本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解题的关键.
20.【答案】解:如图,即为所作.
如图,即为所作.
【解析】分别作出点、、绕点顺时针旋转后的对应点、、,顺次连接即可;
分别连接、、并分别延长到点、、,使得、、,顺次连接、、即可.
此题考查了旋转和位似图形的作图,熟练掌握作图方法是解题的关键.
21.【答案】证明:,
,
又,
∽;
解:∽,
,
,
,
.
【解析】先利用等腰三角形的性质得出,再由可证得∽;
由相似三角形的性质可得出答案.
本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题的关键.
22.【答案】
【解析】解:设每件衣服降价元,则每天销售量增加件,每件商品盈利元.
故答案为:,;
设每件服装降价元,则每件的销售利润为元,平均每天的销售量为件,
依题意得:,
整理得:,
解得:,.
又需要让利于顾客,
.
答:每件服装降价元时,能让利于顾客并且商家平均每天能盈利元.
根据每件服装降价元,那么平均每天可多售出件,可得结论;
设每件服装降价元,则每件的销售利润为元,平均每天的销售量为件,利用商家每天销售该款服装获得的利润每件的销售利润日销售量,即可得出关于的一元二次方程,解之即可得出的值,再结合需要让利于顾客,即可得出每件服装应降价元.
本题考查了一元二次方程的应用以及根的判别式,解题的关键是:找准等量关系,正确列出一元二次方程;牢记“当时,方程无实数根”.
23.【答案】证明:,
,即,
,,
,,
,
,
∽;
证明:如图,
,
,,
由可知,,
,
,
,
在和中,
,
≌,
,
,,
四边形为平行四边形,
,
平行四边形为菱形.
【解析】由等角加同角相等可得,由和的顶角相等,且都是等腰三角形,以此即可证明∽;
根据平行线的性质得,,进而得到,由等腰三角形三线合一的性质可得,再通过证明≌,得到,由对边平行且相等的四边形是平行四边形可证明四边形为平行四边形,最后根据一组邻边相等的平行四边形是菱形即可证明四边形是菱形.
本题主要考查相似三角形的判定、等腰三角形的性质、平行线的性质、全等三角形的判定与性质,熟练菱形的判定方法是解题关键.菱形的判定:菱形定义:一组邻边相等的平行四边形是菱形平行四边形一组邻边相等菱形四条边都相等的四边形是菱形.对角线互相垂直的平行四边形是菱形或“对角线互相垂直平分的四边形是菱形”.
24.【答案】解:;
因为,
所以,
所以,
即,
所以,
所以.
【解析】把分子分母都乘以,然后利用平方差公式计算;
先分母有理化得到,再移项平方得到,接着把变形为,然后利用整体代入的方法计算.
本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.也考查了分母有理化.
25.【答案】
【解析】解:点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
,,
,
故答案为:,;
由题意得,
,
解得:,不合题意,舍去,
当时,的面积等于;
存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为.
由路程速度时间,可直接求解;
由三角形的面积公式可求解;
由题意可得的面积等于面积的,由三角形的面积公式可求解.
本题是四边形综合题,考查了三角形的面积公式,一元二次方程的应用,灵活运用这些性质解决问题是解题的关键.
26.【答案】证明:和分别是等边三角形,
,,
,
,
即,
在和中,
,
≌,
;
解:,
证明:,都是等腰直角三角形,
,,
,
,
,
∽,
,
;
解:如图,连接,
由知∽,
,
,
四边形是正方形,
,
,
四边形是正方形,
,,
,,三点共线.
,
,
;
如图,连接,
由知∽,
,
,
四边形是正方形,
,
,
四边形是正方形,
,,
,,三点共线.
,
,
;
综上,当,,三点共线时,的长度为或.
【解析】证明≌,由全等三角形的性质得出;
证明∽,由相似三角形的性质得出,则可得出结论;
分两种情况画出图形,证明∽,根据相似三角形的判定和性质以及勾股定理即可得出答案.
本题属于四边形综合题,考查了旋转的性质,等腰直角三角形的性质,等边三角形的性质,正方形的性质,相似三角形的判定和性质,全等三角形的判定与性质等知识,解题的关键是正确寻找相似三角形解决问题,学会添加常用辅助线,构造全等三角形解决问题.
第1页,共1页
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 化简的结果是( )
A. B. C. D.
2. 图是伸缩折叠不锈钢晾衣架的实物图,图是它的侧面示意图,与相交于点,,根据图中的数据可得的值为( )
A. B. C. D.
3. 下列计算中,正确的是( )
A. B.
C. D.
4. 如图,∽,,::,则为( )
A.
B.
C.
D.
5. 一元二次方程 的根的情况为( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
6. 某商店将一批夏装降价处理,经过两次降价后,由每件元降至元,求平均每次降价的百分率设平均每次降价的百分率为,可列方程( )
A. B.
C. D.
7. 观察如表,一元二次方程的解的范围是( )
A. B. C. D.
8. 如图,在 中,分别以,为圆心,大于的长为半径画弧,两弧相交于点,,过,两点作直线交于点,交,于点,,下列结论不正确的是( )
A.
B.
C.
D.
9. 如图,矩形的顶点,,顶点在轴的正半轴上作如下操作:对折矩形,使得与重合,得到折痕,把纸片展平;再一次折叠纸片,使点落在上,并使折痕经过点,得折痕同时,得到了线段则点的坐标是( )
A. B. C. D.
10. 如图,在四边形中,,,,点从点出发,以的速度向点运动,点从点同时出发,以相同的速度向点运动,当其中一个动点到达端点时,两个动点同时停止运动设点的运动时间为单位:,下列结论正确的是( )
A. 当时,四边形为矩形
B. 当时,四边形为平行四边形
C. 当时,
D. 当时,或
二、填空题(本大题共6小题,共24.0分)
11. 若,则:______.
12. 若代数式有意义,则的取值范围是______.
13. 若最简根式与是同类二次根式,则 ______ .
14. 若、是方程的两个实数根,则代数式的值为______ .
15. 如图,乐器上的一根弦,两个端点,固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,,之间的距离为______ .
16. 如图,菱形的对角线,相交于点,点为边上一动点不与点,重合,于点,于点,若,,则的最小值为 .
三、解答题(本大题共10小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:.
18. 本小题分
解方程:.
19. 本小题分
如图,在矩形中,点,在对角线上,且,连接,.
求证:.
20. 本小题分
在平面直角坐标系内,的位置如图所示.
将绕点顺时针旋转得到,作出.
以原点为位似中心,在第四象限内作出的位似图形,且与的相似比为:.
21. 本小题分
如图,已知等腰,,点、分别在、上,且.
求证:∽;
如果,,,求的长.
22. 本小题分
一款服装每件进价为元,销售价为元时,每天可售出件经市场调查发现,如果每件服装降价元,那么平均每天可多售出件.
设每件服装降价元,则每天销售量增加______ 件,每件服装盈利______ 元用含的代数式表示;
在让利于顾客的情况下,每件服装降价多少元时,商家平均每天能盈利元?
23. 本小题分
如图,已知和,,,点在边上,,边与相交于点.
求证:∽;
如果,,连结.
求证:四边形是菱形.
24. 本小题分
在解决问题“已知,求的值”时,小明是这样分析与解答的:
因为
所以,所以,
所以,所以.
请你根据小明的分析过程,解决如下问题:
化简:;
若,求的值.
25. 本小题分
如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
填空: ______ , ______ ;用含的代数式表示
当为几秒时,的长度等于.
是否存在某一时刻,使四边形的面积等于面积的?如果存在,求出的值,如果不存在,请说明理由,
26. 本小题分
原题再现:小百合特别喜欢探究数学问题,一天万老师给她这样一个几何问题:
和都是等边三角形,将绕着点旋转到图位置,求证:小百合很快就通过≌,论证了.
请你帮助小百合写出证明过程;
迁移应用:小百合想,把等边和等边都换成等腰直角三角形,将绕着点旋转到图位置,其中,那么和有什么数量关系呢?
请你帮助小百合写出结论,并给出证明;
如图,如果把等腰直角三角形换成正方形,将正方形绕点旋转,若,,在旋转过程中,当,,三点共线时,请直接写出的长度.
答案和解析
1.【答案】
【解析】解:,
故选:.
根据二次根式的性质求出即可.
本题考查了二次根式的性质的应用,主要考查学生的计算能力,题目比较好,难度不大.
2.【答案】
【解析】解:,
∽,
,
,
,
故选:.
由,可得出∽,进而得出,解出即可得出结论.
本题主要考查了三角形相似的判定和性质,熟练掌握相似的判定和性质是解此题的关键.
3.【答案】
【解析】解:.,故计算错误,不符合题意;
B.,故计算错误,不符合题意;
C.,故计算错误,符合题意;
D.,故计算错误,不符合题意;
故选:.
根据算术平方根的含义可判断;
根据二次根式的除法运算可判断;
根据二次根式的乘法运算可判断;
根据二次根式的减法运算可判断.
本题考查了算术平方根的含义,二次根式的加减乘除运算,掌握相应的运算法则是解本题的关键.
4.【答案】
【解析】解:::,
::,
相似比为:,即,,
;
故选:.
根据:的比,可得:的比,利用面积比是相似比的平方,可得,从而可得答案.
本题考查了形似三角形的性质,解题的关键是掌握面积比是相似比的平方.
5.【答案】
【解析】解:,
,
一元二次方程没有实数根,
故选D.
本题考查根的判别式,解题的关键是由根的判别式的正负判断一元二次方程根的情况.
6.【答案】
【解析】解:设平均每次降价的百分率为,根据题意列方程得:
,
故选:.
此题可设平均每次降价的百分率为,那么第一次降价后的单价是原来的,那么第二次降价后的单价是原来的,根据题意列方程解答即可.
本题考查的是平均变化率问题.解决这类问题所用的等量关系一般是:.
7.【答案】
【解析】
【分析】
本题考查了估算一元二次方程的近似解:用列举法估算一元二次方程的近似解,具体方法是:给出一些未知数的值,计算方程两边结果,当两边结果愈接近时,说明未知数的值愈接近方程的根.会估算一元二次方程的近似解是解题的关键.
根据图表数据找出一元二次方程等于时,未知数的值的范围,即可得到答案.
【解答】
解:时,,时,,
一元二次方程的解的范围是,
故选:.
8.【答案】
【解析】解:根据作图可知:垂直平分,
,
四边形是平行四边形,
,,
,
,
≌,
,,故B,C正确;
无法证明,故D错误;
故选:.
根据作图可知:垂直平分,根据线段垂直平分线的性质得到,根据平行四边形的性质得到,,根据全等三角形的性质得到,,故B,C正确;无法证明,故D错误.
本题考查了作图基本作图,垂直平分线的性质,尺规作图,菱形的判定与性质,全等三角形的判定与性质以及勾股定理等知识,掌握菱形的判定与性质是解答本题的关键.
9.【答案】
【解析】解:,,
,
四边形为矩形,,
,
根据折叠的性质可得,,,,
,
如图,过点作于点,
则四边形为矩形,
,,
在中,,
点的坐标为.
故选:.
根据题意可得,由折叠可知,,,得到,过点作于点,,,再根据勾股定理求得,以此即可得到点的坐标.
本题主要考查坐标与图形、折叠的性质、矩形的性质、勾股定理,熟练掌握折叠的性质是解题关键.
10.【答案】
【解析】解:根据题意,可得,,
,,
,,
当四边形为矩形时,,
即,
解得,
故A选项不符合题意;
当四边形为平行四边形,,
即,
解得,
故B选项不符合题意;
当时,分两种情况:
四边形是平行四边形,
此时,
即,
解得,
四边形是等腰梯形,
过点作于点,过点作于点,如图所示:
则,
,,
≌,
,
,
又,
,
解得,
综上,当时,或,
故C选项不符合题意,选项符合题意,
故选:.
根据题意,表示出,,和的长,当四边形为矩形时,根据,列方程求解即可;当四边形为平行四边形,根据,列方程求解即可;当时,分两种情况:四边形是平行四边形,四边形是等腰梯形,分别列方程求解即可.
本题考查了矩形的判定,平行四边形的判定,全等三角形的判定和性质,涉及动点问题,用含的代数式表示出各线段的长是解题的关键.
11.【答案】:
【解析】解:::,
故答案为::.
根据等式的性质,可得答案.
本题考查了比例的性质,利用等式的性质是解题关键.
12.【答案】
【解析】解:代数式有意义,
,
解得:,
故答案为:.
根据有意义得出,再求出答案即可.
本题考查了二次根式有意义的条件,能根据有意义得出是解此题的关键.
13.【答案】
【解析】解:最简根式与是同类二次根式,
,
,
,
故答案为:.
根据同类二次根式的定义可得,然后进行计算即可解答.
本题考查了同类二次根式,最简二次根式,熟练掌握同类二次根式的定义是解题的关键.
14.【答案】
【解析】解:是方程的实数根,
,
,
,
、是方程的两个实数根,
,
.
故答案为:.
先根据一元二次方程根的定义得到,则化为,再利用根与系数的关系得,然后利用整体代入的方法计算.
本题考查了根与系数的关系:若,是一元二次方程的两根时,,也考查了一元二次方程的解.
15.【答案】
【解析】解:弦,点是靠近点的黄金分割点,设,则,
,解方程得,,
点是靠近点的黄金分割点,设,则,
,解方程得,,
,之间的距离为,
故答案为:.
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比.其比值是一个无理数,用分数表示为,由此即可求解.
本题主要考查线段成比例,掌握线段成比例,黄金分割点的定义是解题的关键.
16.【答案】
【解析】解:连接,
四边形是菱形,
,,,
,
于点,于点,
,
四边形是矩形,
,
当取最小值时,的值最小,
当时,最小,
,
,
的最小值为,
故答案为:.
连接,根据菱形的性质得到,,,根据勾股定理得到,根据矩形的性质得到,根据三角形的面积公式即可得到结论.
本题考查了矩形的判定和性质,垂线段最短,菱形的性质,熟练掌握垂线段最短是解题的关键.
17.【答案】解:原式
.
【解析】直接利用二次根式的性质以及绝对值的性质、负整数指数幂的性质分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
18.【答案】解:移项得,
配方得,
即,
开方得,
,.
【解析】本题考查配方法解一元二次方程.
根据配方法即可解.
19.【答案】证明:四边形是矩形,
,.
.
,
,即.
在和中,,
≌,
.
【解析】证明≌,即可得出.
本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解题的关键.
20.【答案】解:如图,即为所作.
如图,即为所作.
【解析】分别作出点、、绕点顺时针旋转后的对应点、、,顺次连接即可;
分别连接、、并分别延长到点、、,使得、、,顺次连接、、即可.
此题考查了旋转和位似图形的作图,熟练掌握作图方法是解题的关键.
21.【答案】证明:,
,
又,
∽;
解:∽,
,
,
,
.
【解析】先利用等腰三角形的性质得出,再由可证得∽;
由相似三角形的性质可得出答案.
本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题的关键.
22.【答案】
【解析】解:设每件衣服降价元,则每天销售量增加件,每件商品盈利元.
故答案为:,;
设每件服装降价元,则每件的销售利润为元,平均每天的销售量为件,
依题意得:,
整理得:,
解得:,.
又需要让利于顾客,
.
答:每件服装降价元时,能让利于顾客并且商家平均每天能盈利元.
根据每件服装降价元,那么平均每天可多售出件,可得结论;
设每件服装降价元,则每件的销售利润为元,平均每天的销售量为件,利用商家每天销售该款服装获得的利润每件的销售利润日销售量,即可得出关于的一元二次方程,解之即可得出的值,再结合需要让利于顾客,即可得出每件服装应降价元.
本题考查了一元二次方程的应用以及根的判别式,解题的关键是:找准等量关系,正确列出一元二次方程;牢记“当时,方程无实数根”.
23.【答案】证明:,
,即,
,,
,,
,
,
∽;
证明:如图,
,
,,
由可知,,
,
,
,
在和中,
,
≌,
,
,,
四边形为平行四边形,
,
平行四边形为菱形.
【解析】由等角加同角相等可得,由和的顶角相等,且都是等腰三角形,以此即可证明∽;
根据平行线的性质得,,进而得到,由等腰三角形三线合一的性质可得,再通过证明≌,得到,由对边平行且相等的四边形是平行四边形可证明四边形为平行四边形,最后根据一组邻边相等的平行四边形是菱形即可证明四边形是菱形.
本题主要考查相似三角形的判定、等腰三角形的性质、平行线的性质、全等三角形的判定与性质,熟练菱形的判定方法是解题关键.菱形的判定:菱形定义:一组邻边相等的平行四边形是菱形平行四边形一组邻边相等菱形四条边都相等的四边形是菱形.对角线互相垂直的平行四边形是菱形或“对角线互相垂直平分的四边形是菱形”.
24.【答案】解:;
因为,
所以,
所以,
即,
所以,
所以.
【解析】把分子分母都乘以,然后利用平方差公式计算;
先分母有理化得到,再移项平方得到,接着把变形为,然后利用整体代入的方法计算.
本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.也考查了分母有理化.
25.【答案】
【解析】解:点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
,,
,
故答案为:,;
由题意得,
,
解得:,不合题意,舍去,
当时,的面积等于;
存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为.
由路程速度时间,可直接求解;
由三角形的面积公式可求解;
由题意可得的面积等于面积的,由三角形的面积公式可求解.
本题是四边形综合题,考查了三角形的面积公式,一元二次方程的应用,灵活运用这些性质解决问题是解题的关键.
26.【答案】证明:和分别是等边三角形,
,,
,
,
即,
在和中,
,
≌,
;
解:,
证明:,都是等腰直角三角形,
,,
,
,
,
∽,
,
;
解:如图,连接,
由知∽,
,
,
四边形是正方形,
,
,
四边形是正方形,
,,
,,三点共线.
,
,
;
如图,连接,
由知∽,
,
,
四边形是正方形,
,
,
四边形是正方形,
,,
,,三点共线.
,
,
;
综上,当,,三点共线时,的长度为或.
【解析】证明≌,由全等三角形的性质得出;
证明∽,由相似三角形的性质得出,则可得出结论;
分两种情况画出图形,证明∽,根据相似三角形的判定和性质以及勾股定理即可得出答案.
本题属于四边形综合题,考查了旋转的性质,等腰直角三角形的性质,等边三角形的性质,正方形的性质,相似三角形的判定和性质,全等三角形的判定与性质等知识,解题的关键是正确寻找相似三角形解决问题,学会添加常用辅助线,构造全等三角形解决问题.
第1页,共1页
同课章节目录
