人教版数学八年级上册 14.1.4 整式的乘法第2课时多项式乘多项式课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.1.4 整式的乘法第2课时多项式乘多项式课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
14.1.4 整式的乘法
第2课时 多项式的乘法
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
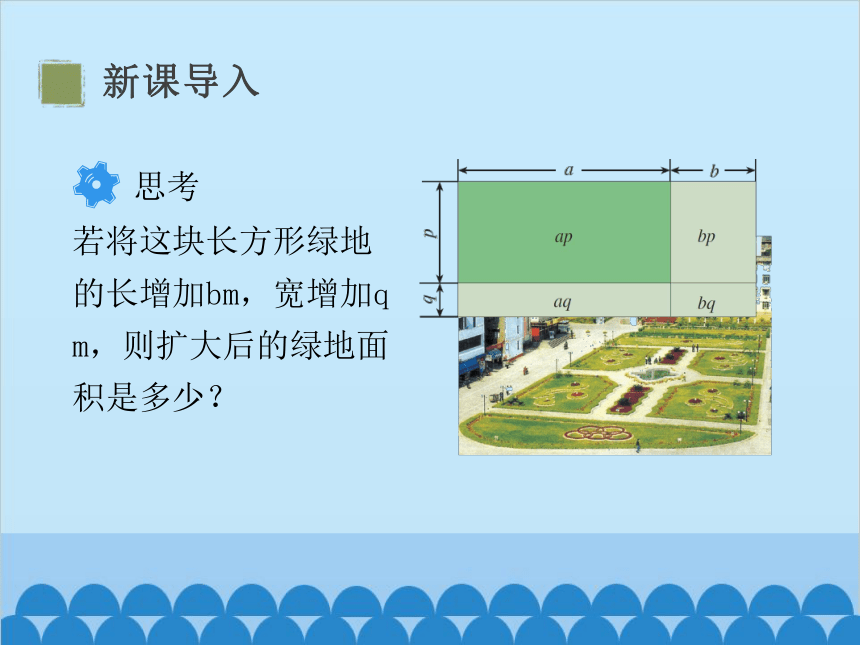
若将这块长方形绿地的长增加bm,宽增加q m,则扩大后的绿地面积是多少?
思考
新课导入
讲授新知
贰
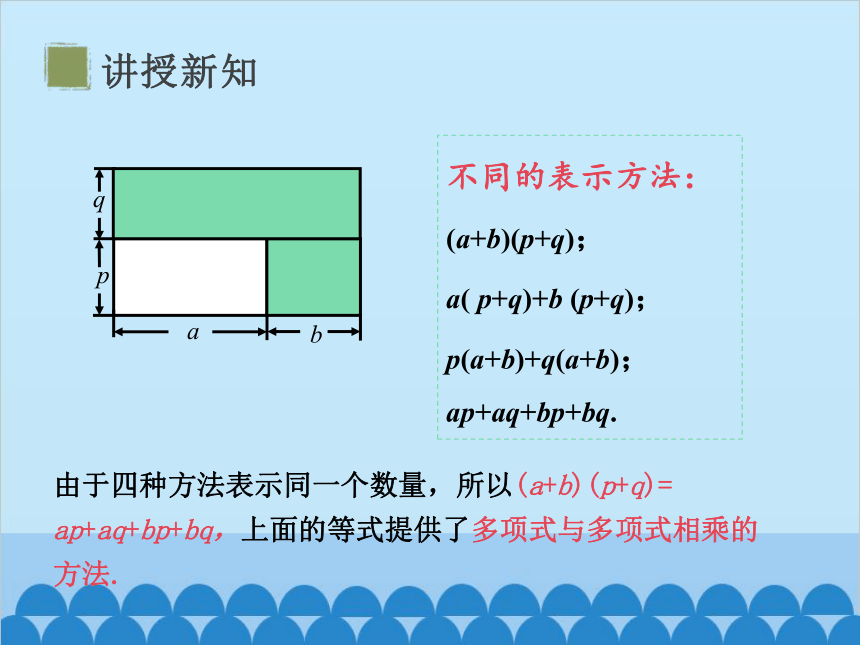
由于四种方法表示同一个数量,所以(a+b)(p+q)= ap+aq+bp+bq,上面的等式提供了多项式与多项式相乘的方法.
不同的表示方法:
(a+b)(p+q);
a( p+q)+b (p+q);
p(a+b)+q(a+b);
ap+aq+bp+bq.
a
p
q
b
讲授新知
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
知识点 多项式乘多项式
讲授新知
1.多项式乘法法则的实质是将多项式与多项式相乘转化为几个单项式相乘的和的形式;
2.多项式与多项式相乘的结果仍为多项式,若有同类项,一定要及时合并同类项,在合并同类项之前,积的项数应该是两个多项式的项数之积;
3.多项式乘法法则也适用于多个多项式相乘,即按顺序先将前两个多项式相乘,再把乘积与第三个多项式相乘,以此类推.
总结归纳
讲授新知
例1 计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).
解:(1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y;
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意
需要注意的几个问题:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式.
范例应用
例2 先化简,再求值:(x-2y)(x+3y)-(2x-y)(x-4y),其中x=-1,y=2.
解:
原式=x2+3xy-2xy-6y2-(2x2-8xy-xy+4y2)
=x2+xy-6y2-(2x2-9xy+4y2)
=x2+xy-6y2-2x2+9xy-4y2
=-x2+10xy-10y2.
当x=-1,y=2时,
原式=-(-1)2+10×(-1)×2-10×22
=-1-20-40
=-61.
范例应用
当堂训练
叁
当堂训练
1.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y-5)=y2+9y-20
C.(m-2)(m+3)=m2+m-6 D.(x-3)(x-6)=x2-9x+18
2.若(x+2)(x-1)=x2+mx+n,则m+n=( )
A.1 B.-2 C.-1 D.23.
3.
B
C
5
6
(-3)
-4
2
(-6)
(-5)
6
(a+b)
ab
观察上面四个等式,你能发现什么规律?
4.计算: (1) (3a+1)(a-2) ; (2) (1-x+y)(-x-y).
解:(1) (3a+1)(a-2)
= 3a a+3a (-2)+1 a+ 1 (-2)
= 3a2-6a+a-2
= 3a2-5a-2 ;
(2) (1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2 .
当堂训练
课堂小结
肆
课堂小结
多项式乘多项式
运算法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
课后作业
基础题:1.课后练习 P102第 1,2题。
提高题:2.请学有余力的同学做同步训练4---5题.
谢
谢
14.1.4 整式的乘法
第2课时 多项式的乘法
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
若将这块长方形绿地的长增加bm,宽增加q m,则扩大后的绿地面积是多少?
思考
新课导入
讲授新知
贰
由于四种方法表示同一个数量,所以(a+b)(p+q)= ap+aq+bp+bq,上面的等式提供了多项式与多项式相乘的方法.
不同的表示方法:
(a+b)(p+q);
a( p+q)+b (p+q);
p(a+b)+q(a+b);
ap+aq+bp+bq.
a
p
q
b
讲授新知
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
知识点 多项式乘多项式
讲授新知
1.多项式乘法法则的实质是将多项式与多项式相乘转化为几个单项式相乘的和的形式;
2.多项式与多项式相乘的结果仍为多项式,若有同类项,一定要及时合并同类项,在合并同类项之前,积的项数应该是两个多项式的项数之积;
3.多项式乘法法则也适用于多个多项式相乘,即按顺序先将前两个多项式相乘,再把乘积与第三个多项式相乘,以此类推.
总结归纳
讲授新知
例1 计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).
解:(1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y;
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意
需要注意的几个问题:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式.
范例应用
例2 先化简,再求值:(x-2y)(x+3y)-(2x-y)(x-4y),其中x=-1,y=2.
解:
原式=x2+3xy-2xy-6y2-(2x2-8xy-xy+4y2)
=x2+xy-6y2-(2x2-9xy+4y2)
=x2+xy-6y2-2x2+9xy-4y2
=-x2+10xy-10y2.
当x=-1,y=2时,
原式=-(-1)2+10×(-1)×2-10×22
=-1-20-40
=-61.
范例应用
当堂训练
叁
当堂训练
1.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y-5)=y2+9y-20
C.(m-2)(m+3)=m2+m-6 D.(x-3)(x-6)=x2-9x+18
2.若(x+2)(x-1)=x2+mx+n,则m+n=( )
A.1 B.-2 C.-1 D.23.
3.
B
C
5
6
(-3)
-4
2
(-6)
(-5)
6
(a+b)
ab
观察上面四个等式,你能发现什么规律?
4.计算: (1) (3a+1)(a-2) ; (2) (1-x+y)(-x-y).
解:(1) (3a+1)(a-2)
= 3a a+3a (-2)+1 a+ 1 (-2)
= 3a2-6a+a-2
= 3a2-5a-2 ;
(2) (1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2 .
当堂训练
课堂小结
肆
课堂小结
多项式乘多项式
运算法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
课后作业
基础题:1.课后练习 P102第 1,2题。
提高题:2.请学有余力的同学做同步训练4---5题.
谢
谢
