11.2与三角形有关的角(2)同步习题精讲课件
文档属性
| 名称 | 11.2与三角形有关的角(2)同步习题精讲课件 |  | |
| 格式 | zip | ||
| 文件大小 | 335.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 15:04:01 | ||
图片预览



文档简介
课件21张PPT。11.2 与三角形有关的角第2课时 三角形的外角11.2 与三角形有关的角1.三角形的一边与另一边的延长线组成的角,叫做三角形的 .
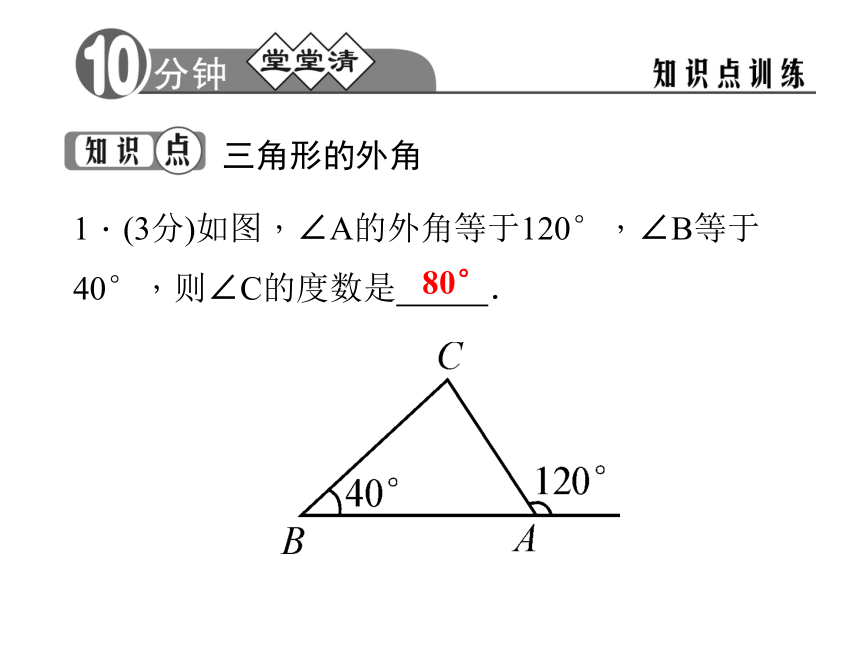
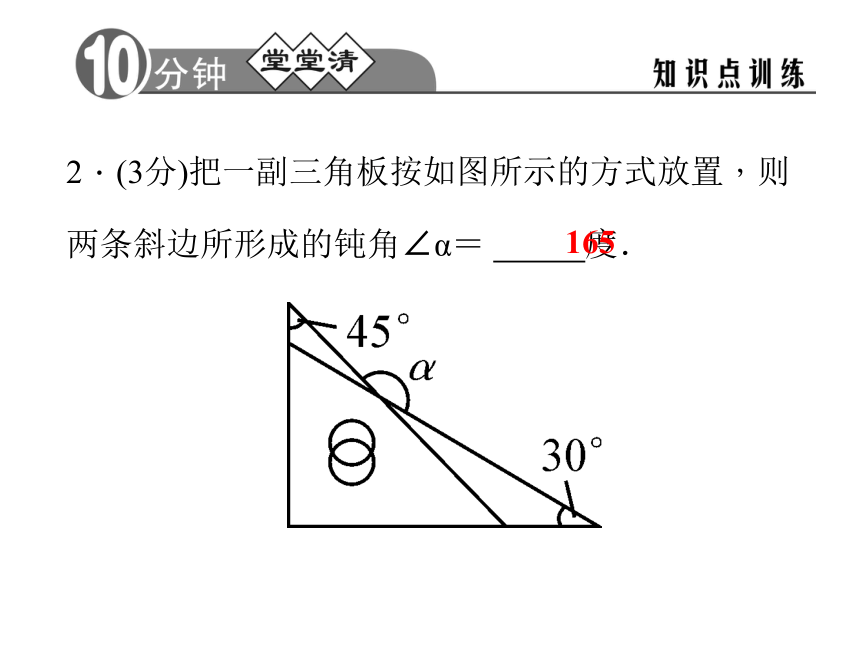
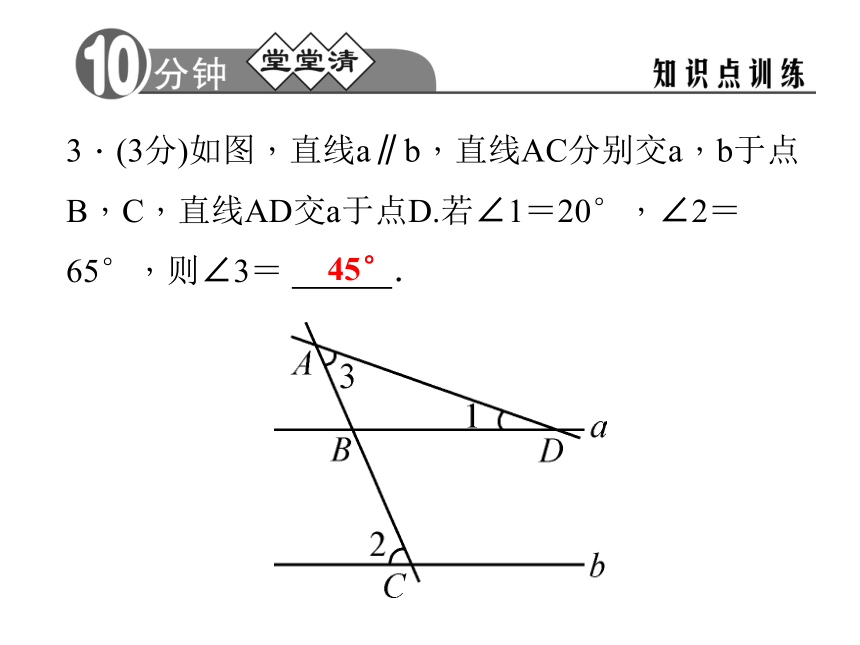
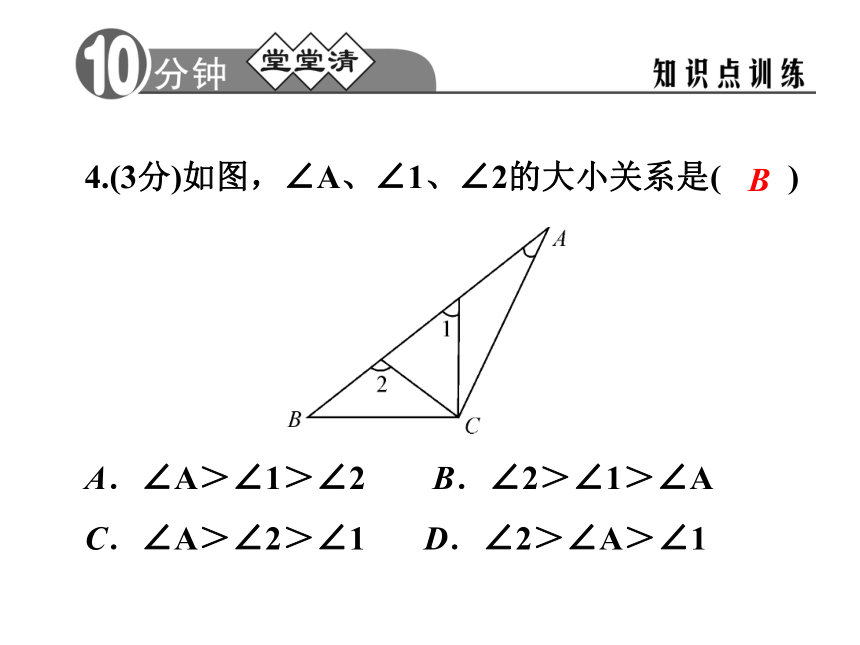
2.三角形的外角等于与它不相邻的 .外角两个内角和三角形的外角 1.(3分)如图,∠A的外角等于120°,∠B等于40°,则∠C的度数是 .80°2.(3分)把一副三角板按如图所示的方式放置,则两条斜边所形成的钝角∠α= 度.1653.(3分)如图,直线a∥b,直线AC分别交a,b于点B,C,直线AD交a于点D.若∠1=20°,∠2=65°,则∠3= .45°4.(3分)如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
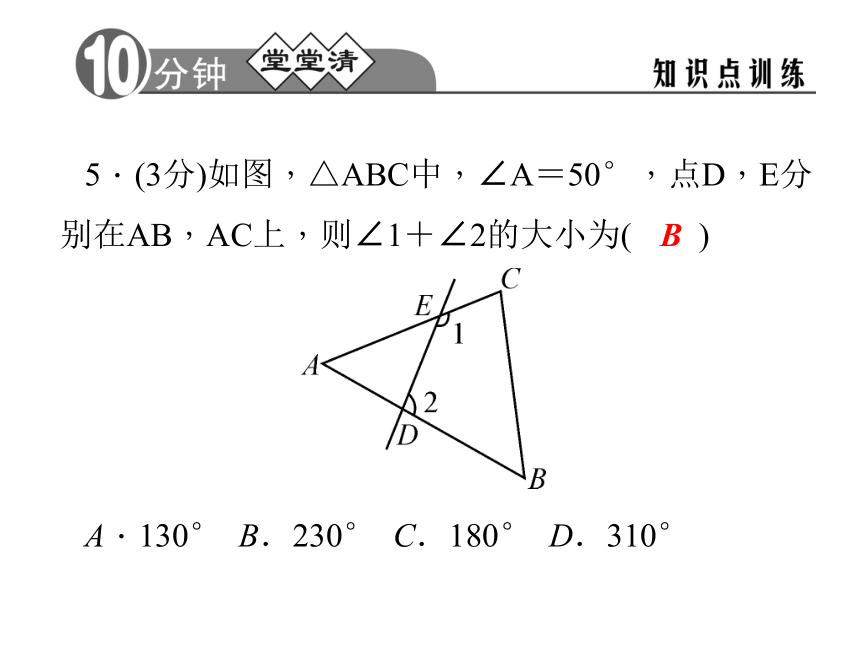
C.∠A>∠2>∠1 D.∠2>∠A>∠1B5.(3分)如图,△ABC中,∠A=50°,点D,E分别在AB,AC上,则∠1+∠2的大小为( )
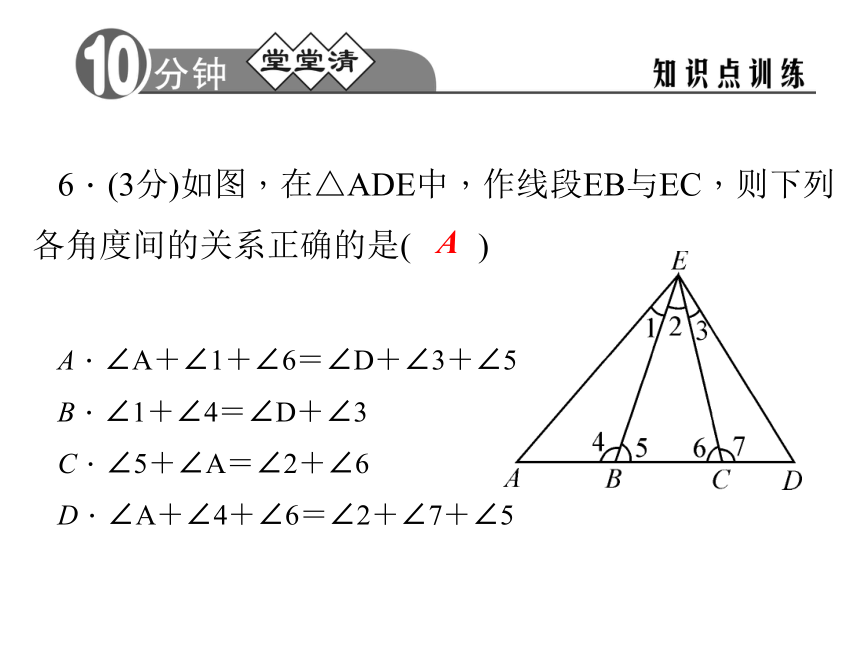
A.130° B.230° C.180° D.310°B6.(3分)如图,在△ADE中,作线段EB与EC,则下列各角度间的关系正确的是( )
A.∠A+∠1+∠6=∠D+∠3+∠5
B.∠1+∠4=∠D+∠3
C.∠5+∠A=∠2+∠6
D.∠A+∠4+∠6=∠2+∠7+∠5A7.(7分)如图,求证:∠BOC=∠A+∠B+∠C.证明:延长BO交AC于点D,因为三角形的一个外角等于与它不相邻的两个内角的和,所以∠BDC=∠A+∠B,∠BOC=∠BDC+∠C,所以∠BOC=∠A+∠B+∠C8.(7分)如图,∠GFC=25°,∠G=20°,∠D=45°,∠A=35°,求∠AED的度数.解:125°9.(8分)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2…∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.
求:∠A1,∠An.解:∠A1= ,
∠An=一、选择题(每小题4分,共12分)
10.已知△ABC中,∠A,∠B,∠C的外角度数之比为2∶3∶4,则这个三角形是( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.等腰三角形
11.如图,∠1、∠2、∠3、∠4恒满足的关系是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4-∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2-∠3CD12.如图,△ABC中,∠B和∠C的外角平分线相交于点D,则∠BDC=( )
A. (90°-∠A)
B.90°-∠A
C. (180°-∠A)
D.180°-∠AC二、填空题(每小题4分,共16分)
13.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3等于 .20°14.如图,则∠α= .
15.如图,∠1,∠2,∠3是△ABC三个不同的外角,则∠1+∠2+∠3= .105°360°16.如图,则∠1+∠2+∠3+∠B= .180°三、解答题(共32分)
17.(10分)如图,△ABC中,∠1=∠2,∠ABC=∠C,∠4=∠C,求∠4的度数.解:设∠1=∠2=x,
在△ABC中,x+2x+2x=180°,
∴x=36°,
∴∠4=2x=2×36°=72°18.(10分)如图,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.解:∠1+∠2=2∠C,理由如下:连接CC′,则由折叠知:
∠ECF=∠EC′F,
∴∠1=∠EC′C+∠ECC′,
∠2=∠FCC′+∠FC′C,
∠1+∠2=2∠C【综合运用】
19.(12分)如图①,有一个图案为五角形ABCDE,你能说明∠A+∠DBE+∠C+∠D+∠E=180°吗?如果B向下移动到AC上[如图②]或AC的另一侧[如图③],上述结论是否依然成立?请说明理由.解:能说明,提示:利用三角形外角性质将其转化在同一个三角形中;结论仍然成立,提示:连接DE,由三角形外角性质易得:∠A+∠C=∠ADE+∠CED,从而这五个角之和刚好为△BDE的内角和
2.三角形的外角等于与它不相邻的 .外角两个内角和三角形的外角 1.(3分)如图,∠A的外角等于120°,∠B等于40°,则∠C的度数是 .80°2.(3分)把一副三角板按如图所示的方式放置,则两条斜边所形成的钝角∠α= 度.1653.(3分)如图,直线a∥b,直线AC分别交a,b于点B,C,直线AD交a于点D.若∠1=20°,∠2=65°,则∠3= .45°4.(3分)如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1B5.(3分)如图,△ABC中,∠A=50°,点D,E分别在AB,AC上,则∠1+∠2的大小为( )
A.130° B.230° C.180° D.310°B6.(3分)如图,在△ADE中,作线段EB与EC,则下列各角度间的关系正确的是( )
A.∠A+∠1+∠6=∠D+∠3+∠5
B.∠1+∠4=∠D+∠3
C.∠5+∠A=∠2+∠6
D.∠A+∠4+∠6=∠2+∠7+∠5A7.(7分)如图,求证:∠BOC=∠A+∠B+∠C.证明:延长BO交AC于点D,因为三角形的一个外角等于与它不相邻的两个内角的和,所以∠BDC=∠A+∠B,∠BOC=∠BDC+∠C,所以∠BOC=∠A+∠B+∠C8.(7分)如图,∠GFC=25°,∠G=20°,∠D=45°,∠A=35°,求∠AED的度数.解:125°9.(8分)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2…∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.
求:∠A1,∠An.解:∠A1= ,
∠An=一、选择题(每小题4分,共12分)
10.已知△ABC中,∠A,∠B,∠C的外角度数之比为2∶3∶4,则这个三角形是( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.等腰三角形
11.如图,∠1、∠2、∠3、∠4恒满足的关系是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4-∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2-∠3CD12.如图,△ABC中,∠B和∠C的外角平分线相交于点D,则∠BDC=( )
A. (90°-∠A)
B.90°-∠A
C. (180°-∠A)
D.180°-∠AC二、填空题(每小题4分,共16分)
13.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3等于 .20°14.如图,则∠α= .
15.如图,∠1,∠2,∠3是△ABC三个不同的外角,则∠1+∠2+∠3= .105°360°16.如图,则∠1+∠2+∠3+∠B= .180°三、解答题(共32分)
17.(10分)如图,△ABC中,∠1=∠2,∠ABC=∠C,∠4=∠C,求∠4的度数.解:设∠1=∠2=x,
在△ABC中,x+2x+2x=180°,
∴x=36°,
∴∠4=2x=2×36°=72°18.(10分)如图,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.解:∠1+∠2=2∠C,理由如下:连接CC′,则由折叠知:
∠ECF=∠EC′F,
∴∠1=∠EC′C+∠ECC′,
∠2=∠FCC′+∠FC′C,
∠1+∠2=2∠C【综合运用】
19.(12分)如图①,有一个图案为五角形ABCDE,你能说明∠A+∠DBE+∠C+∠D+∠E=180°吗?如果B向下移动到AC上[如图②]或AC的另一侧[如图③],上述结论是否依然成立?请说明理由.解:能说明,提示:利用三角形外角性质将其转化在同一个三角形中;结论仍然成立,提示:连接DE,由三角形外角性质易得:∠A+∠C=∠ADE+∠CED,从而这五个角之和刚好为△BDE的内角和
