11.3多边形及其内角和(2)同步习题精讲课件
文档属性
| 名称 | 11.3多边形及其内角和(2)同步习题精讲课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 296.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-25 00:00:00 | ||
图片预览





文档简介
课件19张PPT。11.3 多边形及其内角和第2课时 多边形的内角和11.3 多边形及其内角和1.多边形的内角和等于 .
2.多边形的外角和等于 .(n-2)·180°360°多边形的内角和 1.(4分)一个多边形的内角和是720°,这个多边形的边数是( )
A.4条 B.5条 C.6条 D.7条
2.(4分)若一个多边形的边数为8条,则这个多边形的内角和是( )
A.900° B.540° C.1080° D.360°
3.(4分)若一个多边形增加一条边,那么它的内角和( )
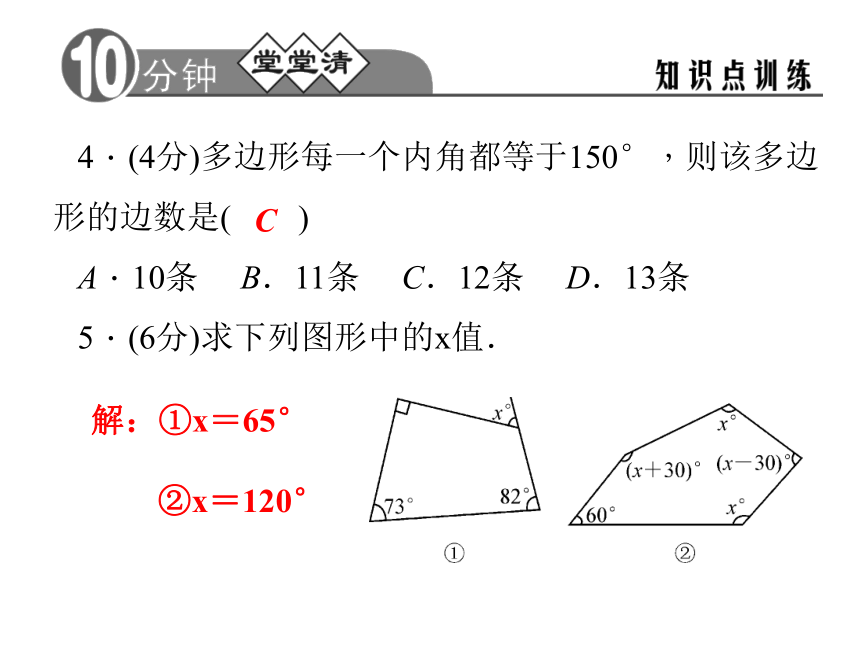
A.增加180° B.增加360° C.减少360° D.不变.CCA4.(4分)多边形每一个内角都等于150°,则该多边形的边数是( )
A.10条 B.11条 C.12条 D.13条
5.(6分)求下列图形中的x值.解:①x=65°
②x=120°
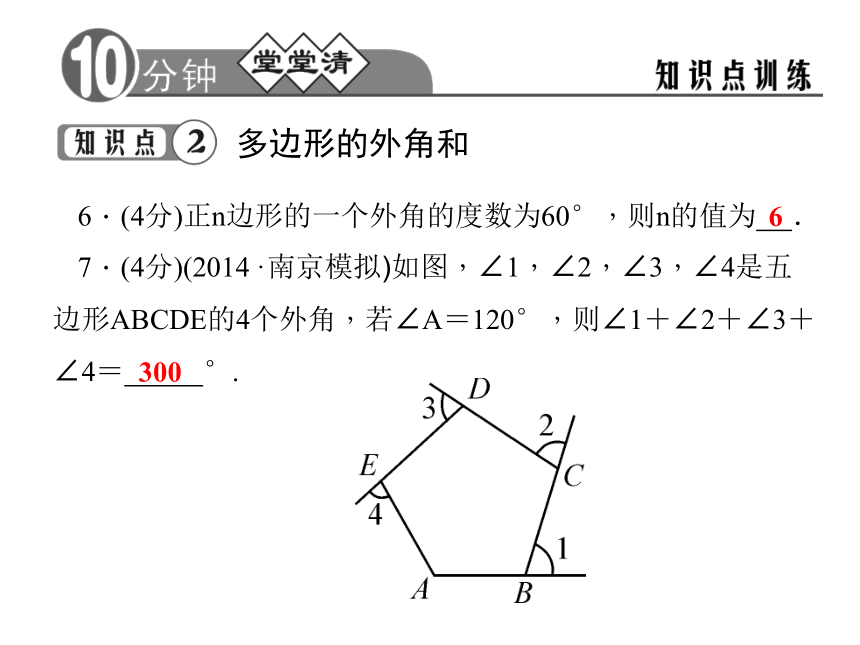
C多边形的外角和 6.(4分)正n边形的一个外角的度数为60°,则n的值为 .
7.(4分)(2014·南京模拟)如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠A=120°,则∠1+∠2+∠3+∠4= °.63008.(4分)一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
9.(6分)一个多边形中,每个内角都相等,并且每个外角都等于它的相邻内角的,求这个多边形的边数及内角和.解:设这个多数形的边数为n.
n=10
内角和:(n-2)·180°=1440°C【易错盘点】
【例】(2013·烟台)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6
C.5或7 D.5或6或7
【错解】A
【错因分析】忽略了分类讨论.
【正解】D 一、选择题(每小题4分,共16分)
10.如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )
A.六边形 B.五边形
C.四边形 D.三角形
11.m边形与n边形内角和的差为720°,则m与n的差为( )
A.2 B.3 C.4 D.5DC12.一个多边形的内角和与外角和之和为2520°,则这个多边形的边数为( )
A.12条 B.13条
C.14条 D.15条
13.在一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角( )
A.1个 B.2个
C.3个 D.4个CC二、填空题(每小题4分,共12分)
14.若凸n边形的内角和为1 260°,则从一个顶点出发引的对角线条数是 .616.如图,分别以四边形ABCD的四个顶点为圆心,R为半径作四个互不相交的圆,则图中阴影部分的面积之和是 .πR215.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了 米.12017.(10分)如图,五边形ABCDE中,AE∥CD,∠A=107°,∠B=121°,求①∠D+∠E的度数;②∠C的度数.解:①∠D+∠E=180°
②∠C=132°
18.(10分)如图,求∠A+∠B+∠C+∠D+E+∠F的度数.解:连接BE.∵∠DOB=∠C+∠D,
∠DOB=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
∵在四边形ABEF中,
∠A+∠ABE+∠BEF+∠F=(4-2)×180°=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.【综合运用】
19.(12分)看图回答:(1)内角和为2 013°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?解:(1)多边形的内角和应为180°的整数倍,所以小明说不可能
(2)十三边形 (3)33°
请使用第89页周周清1
2.多边形的外角和等于 .(n-2)·180°360°多边形的内角和 1.(4分)一个多边形的内角和是720°,这个多边形的边数是( )
A.4条 B.5条 C.6条 D.7条
2.(4分)若一个多边形的边数为8条,则这个多边形的内角和是( )
A.900° B.540° C.1080° D.360°
3.(4分)若一个多边形增加一条边,那么它的内角和( )
A.增加180° B.增加360° C.减少360° D.不变.CCA4.(4分)多边形每一个内角都等于150°,则该多边形的边数是( )
A.10条 B.11条 C.12条 D.13条
5.(6分)求下列图形中的x值.解:①x=65°
②x=120°
C多边形的外角和 6.(4分)正n边形的一个外角的度数为60°,则n的值为 .
7.(4分)(2014·南京模拟)如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠A=120°,则∠1+∠2+∠3+∠4= °.63008.(4分)一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
9.(6分)一个多边形中,每个内角都相等,并且每个外角都等于它的相邻内角的,求这个多边形的边数及内角和.解:设这个多数形的边数为n.
n=10
内角和:(n-2)·180°=1440°C【易错盘点】
【例】(2013·烟台)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6
C.5或7 D.5或6或7
【错解】A
【错因分析】忽略了分类讨论.
【正解】D 一、选择题(每小题4分,共16分)
10.如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )
A.六边形 B.五边形
C.四边形 D.三角形
11.m边形与n边形内角和的差为720°,则m与n的差为( )
A.2 B.3 C.4 D.5DC12.一个多边形的内角和与外角和之和为2520°,则这个多边形的边数为( )
A.12条 B.13条
C.14条 D.15条
13.在一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角( )
A.1个 B.2个
C.3个 D.4个CC二、填空题(每小题4分,共12分)
14.若凸n边形的内角和为1 260°,则从一个顶点出发引的对角线条数是 .616.如图,分别以四边形ABCD的四个顶点为圆心,R为半径作四个互不相交的圆,则图中阴影部分的面积之和是 .πR215.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了 米.12017.(10分)如图,五边形ABCDE中,AE∥CD,∠A=107°,∠B=121°,求①∠D+∠E的度数;②∠C的度数.解:①∠D+∠E=180°
②∠C=132°
18.(10分)如图,求∠A+∠B+∠C+∠D+E+∠F的度数.解:连接BE.∵∠DOB=∠C+∠D,
∠DOB=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
∵在四边形ABEF中,
∠A+∠ABE+∠BEF+∠F=(4-2)×180°=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.【综合运用】
19.(12分)看图回答:(1)内角和为2 013°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?解:(1)多边形的内角和应为180°的整数倍,所以小明说不可能
(2)十三边形 (3)33°
请使用第89页周周清1
