1.2.3 从图象看函数的性质
图片预览



文档简介
课件15张PPT。1.2.3 从图象看函数的性质1.函数的表示方法有__________、_______、_________.
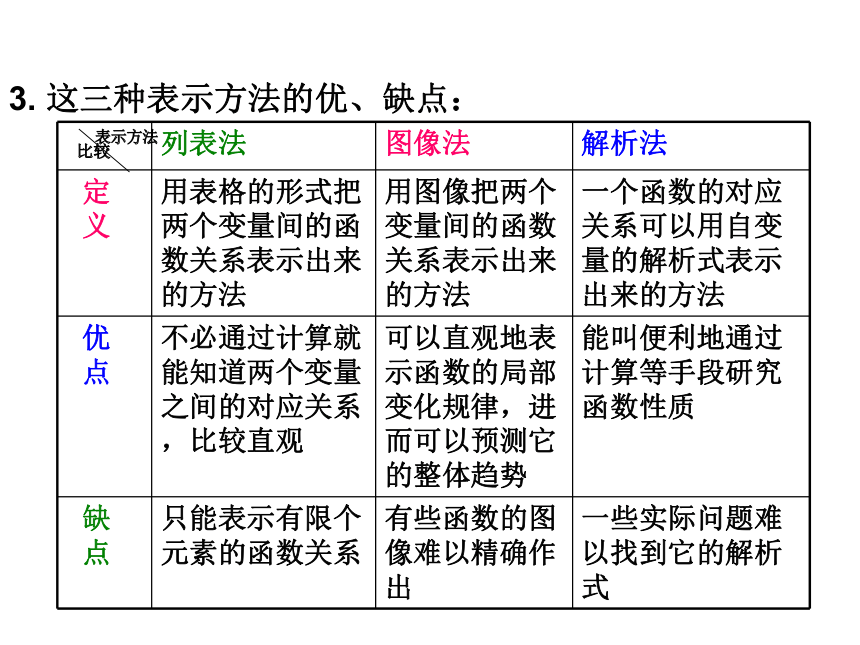
2.作函数图象的描点法的步骤主要有列表,描点,连线.解析法图象法列表法复习:3. 这三种表示方法的优、缺点:-1y=2xy=-0.5x1.奇函数
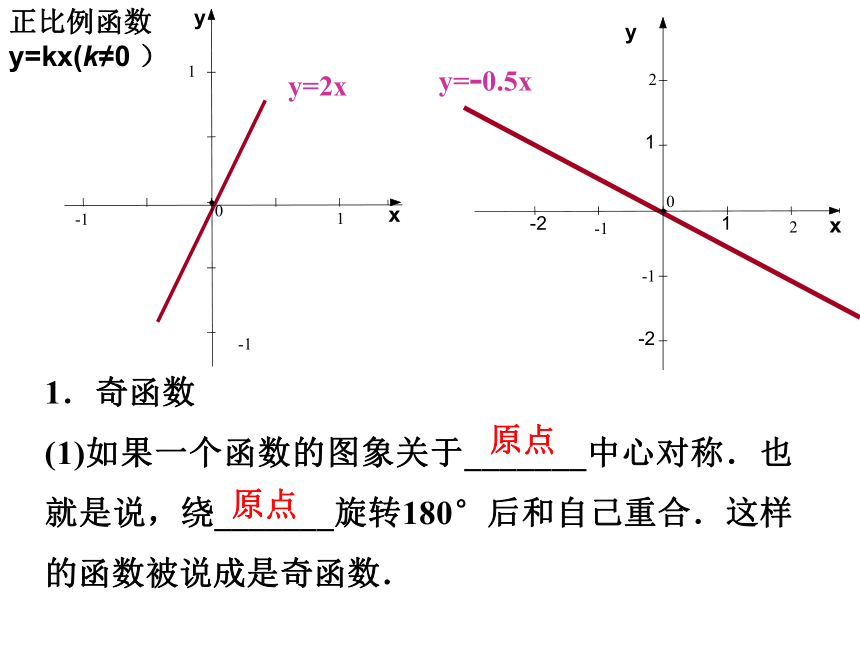
(1)如果一个函数的图象关于_______中心对称.也就是说,绕_______旋转180°后和自己重合.这样的函数被说成是奇函数.原点原点正比例函数y=kx(k≠0 )-11-101y=2x+1y=2xy=2x-1xyy随x的增大而增大,这样的函数叫单调递增函数
y随x的增大而减小,这样的函数叫单调递减函数
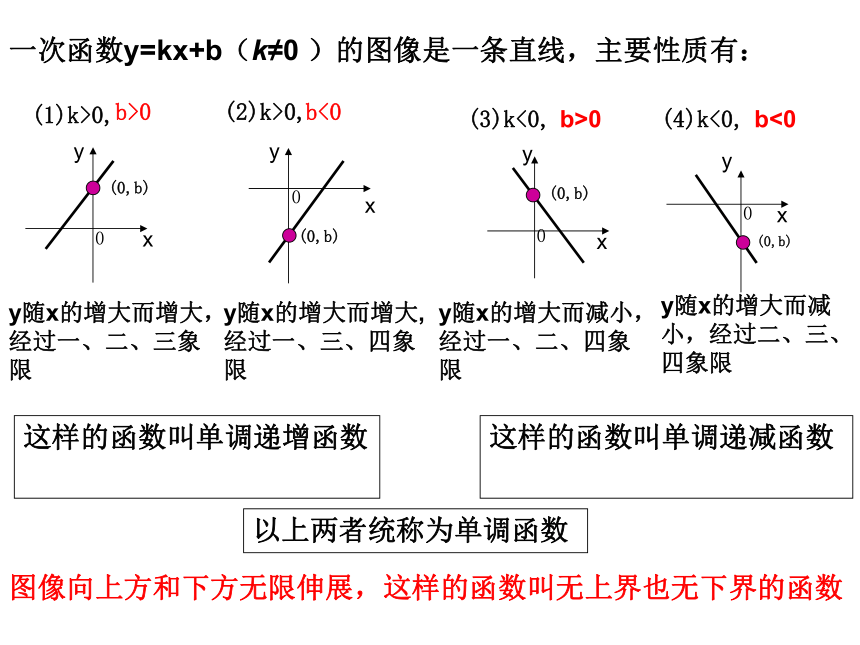
(0,1)(0,-1)(-0.5,0)(0.5,0)图像特点:从左向右看,呈上升趋势图像特点:从左向右看,呈下降趋势一次函数y=kx+b(k≠0 )(1)k>0,(2)k>0,(3)k<0,(4)k<0,(0,b)(0,b)y随x的增大而增大,经过一、二、三象限y随x的增大而增大,
经过一、三、四象限(0,b)(0,b)y随x的增大而减小,经过一、二、四象限y随x的增大而减小,经过二、三、四象限b>0b<0b>0b<0一次函数y=kx+b(k≠0 )的图像是一条直线,主要性质有:这样的函数叫单调递增函数
这样的函数叫单调递减函数
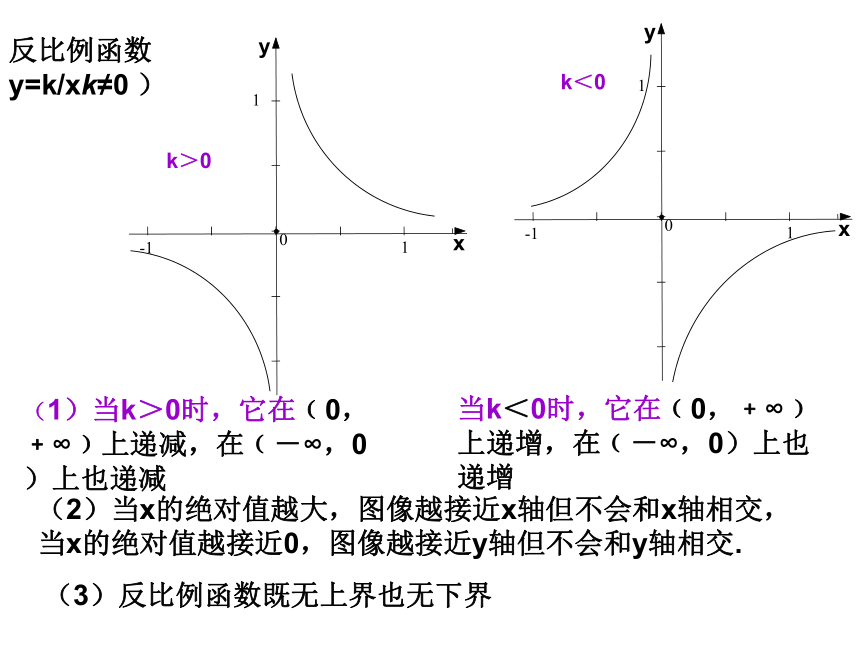
图像向上方和下方无限伸展,这样的函数叫无上界也无下界的函数以上两者统称为单调函数反比例函数y=k/xk≠0 )k>0k<0(2)当x的绝对值越大,图像越接近x轴但不会和x轴相交,当x的绝对值越接近0,图像越接近y轴但不会和y轴相交.(3)反比例函数既无上界也无下界(3)反比例函数的图像关于原点成中心对称图形,这样的函数就是奇函数Y=0.5(4)y=0.5是一个常数函数,它的图像平行于x轴。它的图像也关于y轴对称。(5)图像关于y轴对称的函数就是偶函数。总结:通过函数图象初步认识到可以从以下几个方面来描述函数的基本性质(1)最值-----------最大值和最小值
从图象的最高点、最低点可看出的最值(2)数学研究的函数,可以无上下界(3)单调性---------从图象的上升与下降可看出函数的单调性图像关于原点成中心对称图形,这样的函数就是奇函数图像关于y轴对称的函数就是偶函数。(4) 奇偶性-------从图象关于原点、y轴对称可得出其奇偶性. (1)什么时间气温最高?什么时间气温最低?最高气温和最低气温各是多少?例2如图所示,是某地某天气温随时间变化的函数图象,根据图象,回答在这一天中:(2)20时的气温是多少?(3)什么时间气温为6 ℃?(4)哪段时间内气温不断下降?(5)哪段时间内气温持续不变?(6)哪段时间内气温不断上升?(7)函数在哪些区间上递增,在哪些区间上递减?训练1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据y=f(x)的图象指出它的最大值、最小值及单调区间.练习:课本p:36
1.2.3
2.作函数图象的描点法的步骤主要有列表,描点,连线.解析法图象法列表法复习:3. 这三种表示方法的优、缺点:-1y=2xy=-0.5x1.奇函数
(1)如果一个函数的图象关于_______中心对称.也就是说,绕_______旋转180°后和自己重合.这样的函数被说成是奇函数.原点原点正比例函数y=kx(k≠0 )-11-101y=2x+1y=2xy=2x-1xyy随x的增大而增大,这样的函数叫单调递增函数
y随x的增大而减小,这样的函数叫单调递减函数
(0,1)(0,-1)(-0.5,0)(0.5,0)图像特点:从左向右看,呈上升趋势图像特点:从左向右看,呈下降趋势一次函数y=kx+b(k≠0 )(1)k>0,(2)k>0,(3)k<0,(4)k<0,(0,b)(0,b)y随x的增大而增大,经过一、二、三象限y随x的增大而增大,
经过一、三、四象限(0,b)(0,b)y随x的增大而减小,经过一、二、四象限y随x的增大而减小,经过二、三、四象限b>0b<0b>0b<0一次函数y=kx+b(k≠0 )的图像是一条直线,主要性质有:这样的函数叫单调递增函数
这样的函数叫单调递减函数
图像向上方和下方无限伸展,这样的函数叫无上界也无下界的函数以上两者统称为单调函数反比例函数y=k/xk≠0 )k>0k<0(2)当x的绝对值越大,图像越接近x轴但不会和x轴相交,当x的绝对值越接近0,图像越接近y轴但不会和y轴相交.(3)反比例函数既无上界也无下界(3)反比例函数的图像关于原点成中心对称图形,这样的函数就是奇函数Y=0.5(4)y=0.5是一个常数函数,它的图像平行于x轴。它的图像也关于y轴对称。(5)图像关于y轴对称的函数就是偶函数。总结:通过函数图象初步认识到可以从以下几个方面来描述函数的基本性质(1)最值-----------最大值和最小值
从图象的最高点、最低点可看出的最值(2)数学研究的函数,可以无上下界(3)单调性---------从图象的上升与下降可看出函数的单调性图像关于原点成中心对称图形,这样的函数就是奇函数图像关于y轴对称的函数就是偶函数。(4) 奇偶性-------从图象关于原点、y轴对称可得出其奇偶性. (1)什么时间气温最高?什么时间气温最低?最高气温和最低气温各是多少?例2如图所示,是某地某天气温随时间变化的函数图象,根据图象,回答在这一天中:(2)20时的气温是多少?(3)什么时间气温为6 ℃?(4)哪段时间内气温不断下降?(5)哪段时间内气温持续不变?(6)哪段时间内气温不断上升?(7)函数在哪些区间上递增,在哪些区间上递减?训练1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据y=f(x)的图象指出它的最大值、最小值及单调区间.练习:课本p:36
1.2.3
