1.2.4　从解析式看函数的性质

课件20张PPT。1.2.4　从解析式看函数的性质1．从函数图象上看，从左到右，图象呈______趋势就是增函数．如图（1）
上升下降2．从函数图象上看，从左到右，图象呈______趋势就是减函数．原点(0,0)y轴2．若函数的图象，关于_______ 对称，就是奇函数，如图（3）；若函数的图象，关于_______对称，就是偶函数，如图（4）．1．上界和下界
(1)如果有实数B使得___________对一切x∈D成立，称B是函数f的一个上界(upper bound)；如果有实数A使得__________对一切x∈D成立，称A是函数f的一个下界(lower bound)，其中D是函数f(x)的定义域．
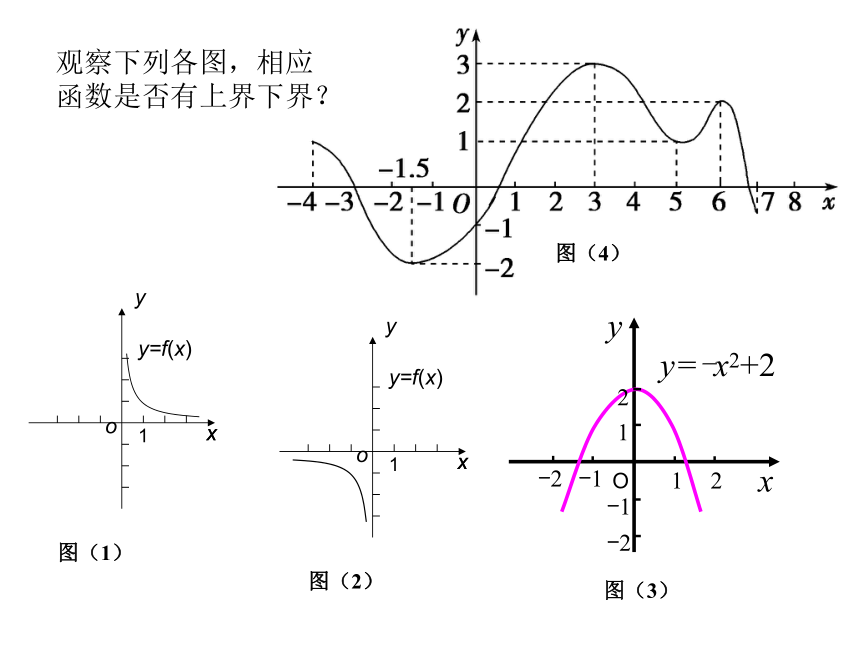
(2)____________________的函数叫有界函数(bounded fun_ction)，否则叫无界函数(unbounded fun_ction)．f(x)≤Bf(x)≥A有上界又有下界xxyo1y=f(x)图（2）观察下列各图，相应函数是否有上界下界？图（4）2．函数的最大(小)值定义
设D是函数f(x)的定义域．
(1)如果有a∈D，使得不等式_____________对一切x∈D成立，就说f(x)在x＝a处取到最大值M＝f(a)，称M为f(x)的最大值，_____为f(x)的最大值点．
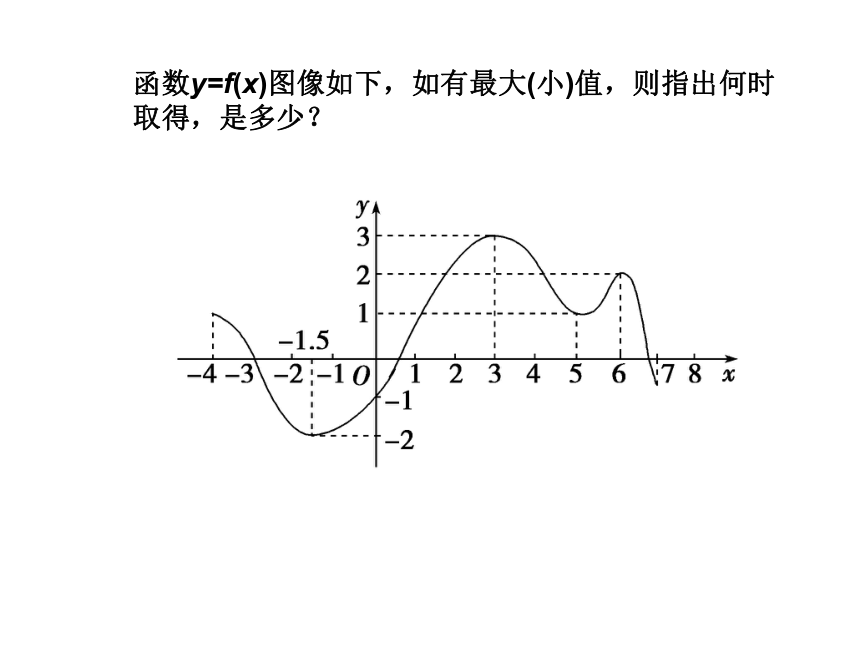
(2)如果有b∈D，使得不等式___________对一切x∈D成立，就说f(x)在x＝b处取到最小值m＝f(b)，称m为f(x)的最小值，_______为f(x)的最小值点．f(x)≤f(a)af(x)≥f(b)b函数y=f(x)图像如下，如有最大(小)值，则指出何时取得，是多少？思考感悟
（1）最大值是不是上界？上界是不是最大值？3．函数的单调性定义
设D为函数f(x)的定义域，I是D的一个非空子集．
(1)如果对于I上任意两个值x1，x2，当__________时都有___________，那么就说f(x)是区间I上的递增函数．反映在图象上，由左到右，图象连续_______．如下图：
x1下降x1f(x2)(3)如果函数y＝f(x)是区间I上的递增函数或递减函数，就说f(x)在I上严格单调，_______叫作f(x)的严格单调区间．区间Iy思考感悟
（2）对于函数y＝x2，令x1＝－1，x2＝2时有f(x1)＜f(x2)，为什么不是增函数？
提示：x1＝－1，x2＝2，只是两个特殊的自变量的值，不是“任意”的两个值，不符合单调性的定义．4．单调性的证明【思路点拨】　先利用单调性的定义判断函数在[1,3]上的单调性，再求函数的最值．【点评】　先证明或判断函数的单调性，再结合区间端点对应的函数值大小得出最值． 已知f(x)是定义在(0，＋∞)上的减函数，实数a满足f(a＋1)【思路点拨】　借助函数单调性，“剥掉”函数符号“f”，转化为整式不等式求解．方法技巧
1．判断函数单调性的方法有定义法、图象法、复合函数法，两个函数和(差)的单调性的判断，增＋增＝增，减＋减＝减，增－减＝增，减－增＝减．如例1，例3.
2．函数的最值与单调性的关系
若函数在闭区间[a，b]上是减函数，则f(x)在[a，b]上的最大值为f(a)，最小值为f(b)；
若函数在闭区间[a，b]上是增函数，则f(x)在[a，b]上的最大值为f(b)，最小值为f(a)．如例2.失误防范
1．求函数单调区间一定要求定义域，单调区间是定义域的子集．
2．求函数的最值，要注意定义域的开与闭.作业：1.证明：函数 在 上为单调递增函数，并求出
函数的最大（小）值。2.写出函数 的单调递增，递
减区间并求出函数的最大（小）值。