2.1.2 指数函数及其性质(全课时,57PPT)
文档属性
| 名称 | 2.1.2 指数函数及其性质(全课时,57PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-27 09:35:53 | ||
图片预览








文档简介
(共106张PPT)
2.1.2 指数函数及其性质
在印度有一个古老的传说:舍罕王
打算奖赏国际象棋的发明人--宰相
西萨·班·达依尔。国王问他想要什么,
他对国王说:"陛下,请您在这棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!"国王觉得这要求太容易满足了,命令给他这些麦粒。
当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求。
1.棋盘上的麦粒
总数为:=18446744073709551615(粒) ,1000粒约40克
麦粒有7000多亿吨(现每年全球的小麦总量约6.5亿吨)
问题引入
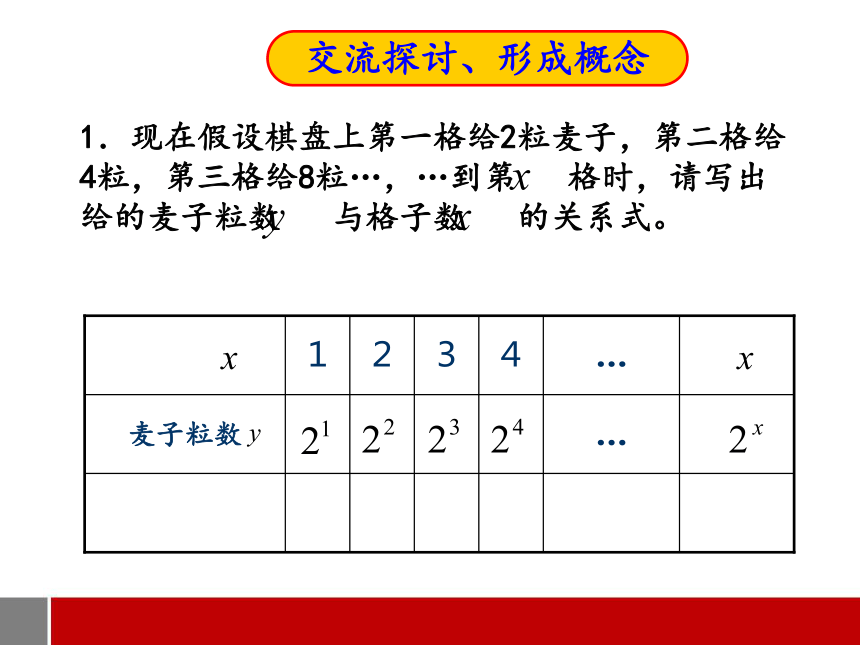
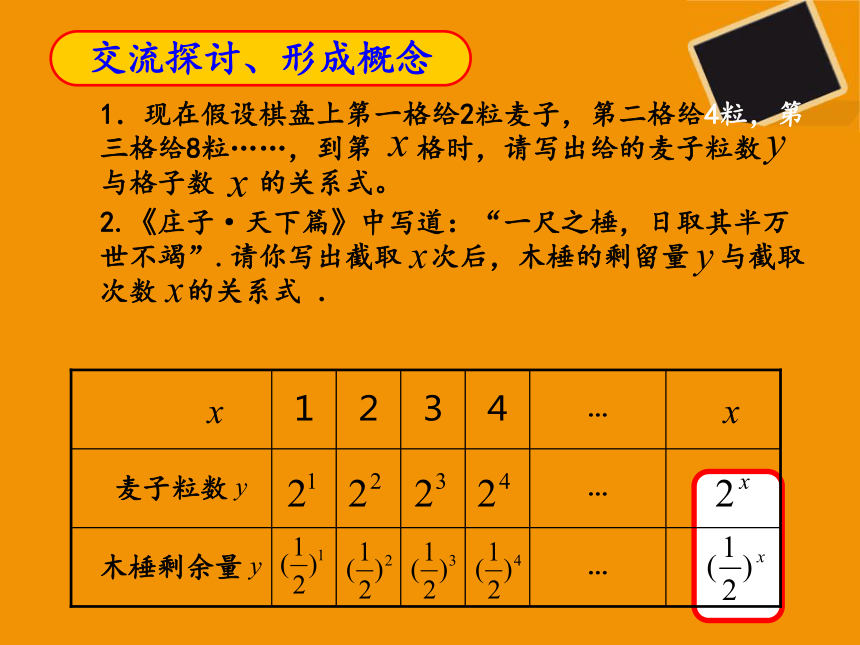
1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒…,…到第 格时,请写出给的麦子粒数 与格子数 的关系式。
交流探讨、形成概念
…
麦子粒数
…
4
3
2
1
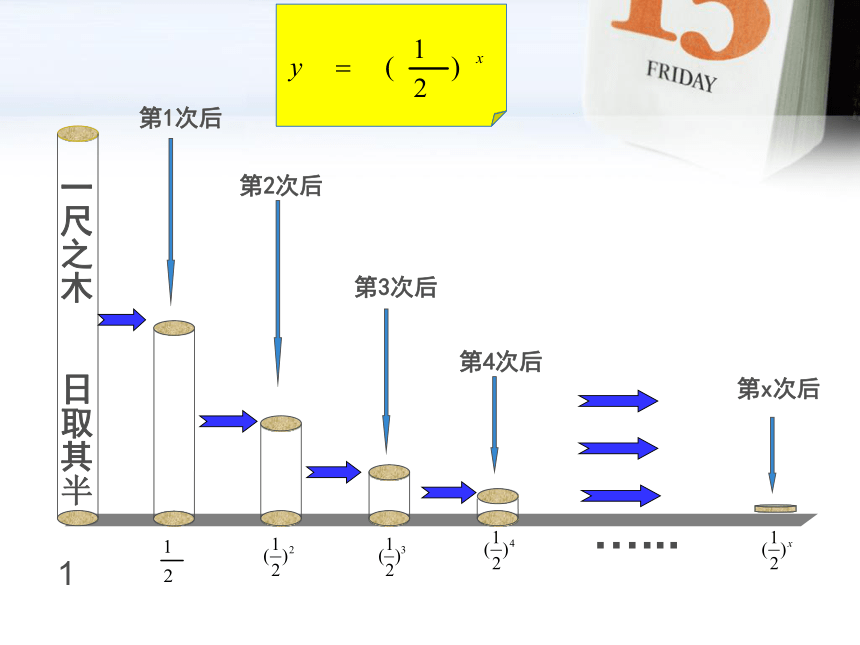
2.《庄子 天下篇》
庄 子
问题2 :《庄子.逍遥游》记载:一尺之椎,日取其半,万世不竭.
意思是一尺长的木棒,一天截取一半,很长时间也截取不完.
这样的一个木棒截取 x 次,剩余长度y与x的关系是
…...
一尺之木 日取其半
第1次后
第2次后
第3次后
第4次后
第x次后
1
2.《庄子·天下篇》中写道:“一尺之棰,日取其半万世不竭”.请你写出截取 次后,木棰的剩留量 与截取次数 的关系式 .
1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒……,到第 格时,请写出给的麦子粒数 与格子数 的关系式。
交流探讨、形成概念
…
木棰剩余量
…
麦子粒数
…
4
3
2
1
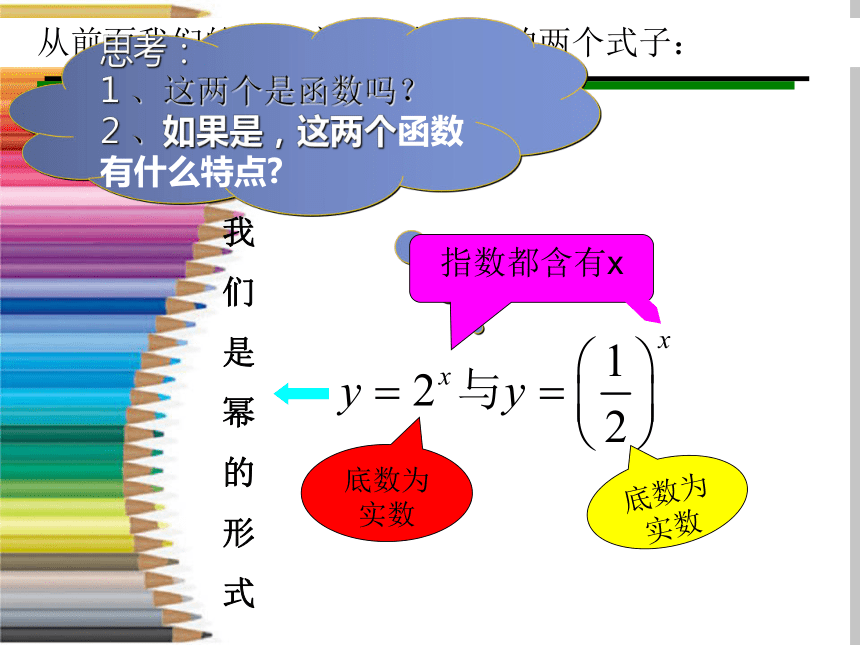
从前面我们的两个实例抽象得到的两个式子:
思考:
1 、这两个是函数吗?
2 、如果是,这两个函数有什么特点
底数为实数
底数为实数
指数都含有x
我
们
是
幂
的
形
式
指数函数的定义:
形如y = (a 0,且a 1)的函数叫做指数函数,其中x是自变量 .
为何规定a 0,且a 1
函数的定义域是R
课本58页练习 2
当a 0时,ax 对有些数会没有意义,如(-2) ,0 等都没有意义;
而当a=1时,函数值y恒等于1,没有研究的必要.
记住:在y= 中a一定大于零!
为何规定a 0,且a 1
0
1
a
为了避免上述各种情况,所以规定a>0且a 1。
指数函数的特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1;
④只有一项ax .
说明
概念理解
例、指出下面哪个函数是指数函数:
是
否
否
是
(1)当k=1时,是;
(2)当k≠1时,否。
思考:
反思:
指数函数的解析式 y=
中,
的系数是1.
有些函数貌似指数函数,实际上却不是,
如:
( a>0 且 a
1,k
Z);
有些函数看起来不像指数函数,实际上却是,
如:
因为它可以化为
【例1】 函数y=(a2-3a+3)ax是指数函数,求a的值.
全优49页典例剖析
研究函数的一般思路:
研究函数的一般方法是:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
探求新知、深化理解
特殊点
定义域
奇偶性
单调性
值域
对称性
探求新知、深化理解
在同一坐标系中画出下列函数的图象(可用描点法,也可借助科学计算器或计算机).
已知函数的解析式,怎么得到函数的图象,一般用什么方法?
列表、描点、连线作图
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1/2 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
1
x
y
o
1
2
3
-1
-2
-3
当a>1时, 的大致图像如下图:
x
y
0
y=1
y=ax
(a>1)
(0,1)
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
y
0
(0x
y=1
y=ax
(0,1)
当0图象和性质:
a>1 0图
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
答案:A
全优96页
2.函数y=ax-3+3(a>0且a≠1)的图象恒过定点__________.
【答案】(3,4)
全优49页变式训练
全优96页1
全优50页能力提高
全优52页变式训练
全优96页
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答问题:
问:从图形的对称性上看,右边函数图像有什么对称特征?
指数函数 与 的图像关于y轴对称;
X
O
Y
Y=1
y=3X
y = 2 x
①当a>1时, 的图象随着a由小变大会有什么样的变化?
②当0①当a>1时, 的图象随着a由小变大会有越靠近y轴;
②当0只看第一象限!
练习、此图是①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A a<b <1 < c < d
B b<a <1 < d < c
C 1<a <b< c < d
D a<b <1 <d < c
①
②
③
④
例6. 已知指数函数y=ax(a>0,且a≠1)的图象经过点(3, ),求f(0),f(1),f(-3)的值.
解:
∵ f(x)=ax的图象过点(3,π)
例7. 比较下列各题中两个值的大小:
(1)1.72.5,1.73;
(2)0.8-0.1,0.8-0.2;
(3)1.70.3,0.93.1.
解:(1)1.72.5、1.73可以看作函数y=1.7x的两个函数值.
∵底数1.7>1,
∴y=1.7x在R上是增函数,
∵2.5<3,
∴1.72.5<1.73 ,
即: 1.72.5<1.73 .
解:(2)0.8-0.1、0.8-0.2可以看作函数y=0.8x的两个函数值.
∵底数0<0.8<1,
∴y=0.8x在R上是减函数,
∵-0.1>-0.2,
∴0.8-0.1<0.8-0.2,
即: 0.8-0.1<0.8-0.2.
解:(3) ∵1.70.3>1.70=1,
0.93.1<0.90=1,
∴1.70.3>1>0.93.1,
即: 1.70.3>1>0.93.1.
小结:比较指数大小的方法:
①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论。
②、中间媒介法:用别的数如为媒介(如1等)。数的特征是不同底不同指。
课本59页习题A7,8 60页B4
【例1】 比较下列各题中两个值的大小:(3)1.40.1与0.90.3.
(3)分别构造函数y=1.4x与y=0.9x.
∵1.4>1,0<0.9<1,∴y=1.4x与y=0.9x
在(-∞,+∞)上分别为增函数和减函数.
∵0.1>0,∴1.40.1>1.40=1.
∵0.3>0,∴0.90.3<0.90=1,
∴1.40.1>1>0.90.3,∴1.40.1>0.90.3.
全优51页典例剖析
全优52页变式训练
2.(2)已知0.2x<25,求实数x的取值范围.
全优52页变式训练
全优53页基础夯实
全优50页基础夯实
【例2】 如果a2x+1≤ax-5(a>0且a≠1),求x的取值范围.
解:(1)当0∴2x+1≥x-5,解得x≥-6.
(2)当a>1时,由于a2x+1≤ax-5,
∴2x+1≤x-5,解得x≤-6.
综上所述,当01时,x的取值范围是{x|x≤-6}.
全优52页典例剖析
例8.截止到1999年底,我国人口约13亿.如果今后将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
解:设今后人口年平均增长率为1%,经过x年后,我国人口数为y亿.
1999年底,我国人口约为13亿;
经过1年(即2000年),人口数为
13+13×1%=13×(1+1%)(亿);
经过2年(即2001年),人口数为
13×(1+1%)+13×(1+1%)×1%
=13×(1+1%)2(亿);
经过3年(即2002年),人口数为
13×(1+1%)2+13×(1+1%)2×1%
=13×(1+1%)3(亿);
……
所以,经过x年,人口数为
y=13×(1+1%)x=13×1.01x(亿).
当x=20时,
y=13×1.0120≈16(亿).
所以,经过20年后,我国人口数最多为16亿.
课本58页练习 3
课本59页习题A6
课本60页习题B2
全优49页典例剖析
全优49页变式训练
全优97页
全优53页基础夯实
答案:D
全优97页
3.若函数f(x)=e-(x-u)2的最大值为m,且f(x)是偶函数,则m+u=________.
解析:∵f(-x)=f(x),
∴e-(x+u)2=e-(x-u)2,
∴(x+u)2=(x-u)2,
∴u=0,∴f(x)=e-x2.
∵x2≥0,∴-x2≤0,∴0<e-x2≤1,
∴m=1,∴m+u=1+0=1.
答案:1
全优97页
全优53页基础夯实
全优96页
全优97页
全优53页能力提高
2.1.2 指数函数及其性质
在印度有一个古老的传说:舍罕王
打算奖赏国际象棋的发明人--宰相
西萨·班·达依尔。国王问他想要什么,
他对国王说:"陛下,请您在这棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!"国王觉得这要求太容易满足了,命令给他这些麦粒。
当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求。
1.棋盘上的麦粒
总数为:=18446744073709551615(粒) ,1000粒约40克
麦粒有7000多亿吨(现每年全球的小麦总量约6.5亿吨)
问题引入
1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒…,…到第 格时,请写出给的麦子粒数 与格子数 的关系式。
交流探讨、形成概念
…
麦子粒数
…
4
3
2
1
2.《庄子 天下篇》
庄 子
问题2 :《庄子.逍遥游》记载:一尺之椎,日取其半,万世不竭.
意思是一尺长的木棒,一天截取一半,很长时间也截取不完.
这样的一个木棒截取 x 次,剩余长度y与x的关系是
…...
一尺之木 日取其半
第1次后
第2次后
第3次后
第4次后
第x次后
1
2.《庄子·天下篇》中写道:“一尺之棰,日取其半万世不竭”.请你写出截取 次后,木棰的剩留量 与截取次数 的关系式 .
1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒……,到第 格时,请写出给的麦子粒数 与格子数 的关系式。
交流探讨、形成概念
…
木棰剩余量
…
麦子粒数
…
4
3
2
1
从前面我们的两个实例抽象得到的两个式子:
思考:
1 、这两个是函数吗?
2 、如果是,这两个函数有什么特点
底数为实数
底数为实数
指数都含有x
我
们
是
幂
的
形
式
指数函数的定义:
形如y = (a 0,且a 1)的函数叫做指数函数,其中x是自变量 .
为何规定a 0,且a 1
函数的定义域是R
课本58页练习 2
当a 0时,ax 对有些数会没有意义,如(-2) ,0 等都没有意义;
而当a=1时,函数值y恒等于1,没有研究的必要.
记住:在y= 中a一定大于零!
为何规定a 0,且a 1
0
1
a
为了避免上述各种情况,所以规定a>0且a 1。
指数函数的特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1;
④只有一项ax .
说明
概念理解
例、指出下面哪个函数是指数函数:
是
否
否
是
(1)当k=1时,是;
(2)当k≠1时,否。
思考:
反思:
指数函数的解析式 y=
中,
的系数是1.
有些函数貌似指数函数,实际上却不是,
如:
( a>0 且 a
1,k
Z);
有些函数看起来不像指数函数,实际上却是,
如:
因为它可以化为
【例1】 函数y=(a2-3a+3)ax是指数函数,求a的值.
全优49页典例剖析
研究函数的一般思路:
研究函数的一般方法是:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
探求新知、深化理解
特殊点
定义域
奇偶性
单调性
值域
对称性
探求新知、深化理解
在同一坐标系中画出下列函数的图象(可用描点法,也可借助科学计算器或计算机).
已知函数的解析式,怎么得到函数的图象,一般用什么方法?
列表、描点、连线作图
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1/2 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
1
x
y
o
1
2
3
-1
-2
-3
当a>1时, 的大致图像如下图:
x
y
0
y=1
y=ax
(a>1)
(0,1)
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
y
0
(0
y=1
y=ax
(0,1)
当0
a>1 0
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
答案:A
全优96页
2.函数y=ax-3+3(a>0且a≠1)的图象恒过定点__________.
【答案】(3,4)
全优49页变式训练
全优96页1
全优50页能力提高
全优52页变式训练
全优96页
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答问题:
问:从图形的对称性上看,右边函数图像有什么对称特征?
指数函数 与 的图像关于y轴对称;
X
O
Y
Y=1
y=3X
y = 2 x
①当a>1时, 的图象随着a由小变大会有什么样的变化?
②当0
②当0
练习、此图是①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A a<b <1 < c < d
B b<a <1 < d < c
C 1<a <b< c < d
D a<b <1 <d < c
①
②
③
④
例6. 已知指数函数y=ax(a>0,且a≠1)的图象经过点(3, ),求f(0),f(1),f(-3)的值.
解:
∵ f(x)=ax的图象过点(3,π)
例7. 比较下列各题中两个值的大小:
(1)1.72.5,1.73;
(2)0.8-0.1,0.8-0.2;
(3)1.70.3,0.93.1.
解:(1)1.72.5、1.73可以看作函数y=1.7x的两个函数值.
∵底数1.7>1,
∴y=1.7x在R上是增函数,
∵2.5<3,
∴1.72.5<1.73 ,
即: 1.72.5<1.73 .
解:(2)0.8-0.1、0.8-0.2可以看作函数y=0.8x的两个函数值.
∵底数0<0.8<1,
∴y=0.8x在R上是减函数,
∵-0.1>-0.2,
∴0.8-0.1<0.8-0.2,
即: 0.8-0.1<0.8-0.2.
解:(3) ∵1.70.3>1.70=1,
0.93.1<0.90=1,
∴1.70.3>1>0.93.1,
即: 1.70.3>1>0.93.1.
小结:比较指数大小的方法:
①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论。
②、中间媒介法:用别的数如为媒介(如1等)。数的特征是不同底不同指。
课本59页习题A7,8 60页B4
【例1】 比较下列各题中两个值的大小:(3)1.40.1与0.90.3.
(3)分别构造函数y=1.4x与y=0.9x.
∵1.4>1,0<0.9<1,∴y=1.4x与y=0.9x
在(-∞,+∞)上分别为增函数和减函数.
∵0.1>0,∴1.40.1>1.40=1.
∵0.3>0,∴0.90.3<0.90=1,
∴1.40.1>1>0.90.3,∴1.40.1>0.90.3.
全优51页典例剖析
全优52页变式训练
2.(2)已知0.2x<25,求实数x的取值范围.
全优52页变式训练
全优53页基础夯实
全优50页基础夯实
【例2】 如果a2x+1≤ax-5(a>0且a≠1),求x的取值范围.
解:(1)当0
(2)当a>1时,由于a2x+1≤ax-5,
∴2x+1≤x-5,解得x≤-6.
综上所述,当0
全优52页典例剖析
例8.截止到1999年底,我国人口约13亿.如果今后将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
解:设今后人口年平均增长率为1%,经过x年后,我国人口数为y亿.
1999年底,我国人口约为13亿;
经过1年(即2000年),人口数为
13+13×1%=13×(1+1%)(亿);
经过2年(即2001年),人口数为
13×(1+1%)+13×(1+1%)×1%
=13×(1+1%)2(亿);
经过3年(即2002年),人口数为
13×(1+1%)2+13×(1+1%)2×1%
=13×(1+1%)3(亿);
……
所以,经过x年,人口数为
y=13×(1+1%)x=13×1.01x(亿).
当x=20时,
y=13×1.0120≈16(亿).
所以,经过20年后,我国人口数最多为16亿.
课本58页练习 3
课本59页习题A6
课本60页习题B2
全优49页典例剖析
全优49页变式训练
全优97页
全优53页基础夯实
答案:D
全优97页
3.若函数f(x)=e-(x-u)2的最大值为m,且f(x)是偶函数,则m+u=________.
解析:∵f(-x)=f(x),
∴e-(x+u)2=e-(x-u)2,
∴(x+u)2=(x-u)2,
∴u=0,∴f(x)=e-x2.
∵x2≥0,∴-x2≤0,∴0<e-x2≤1,
∴m=1,∴m+u=1+0=1.
答案:1
全优97页
全优53页基础夯实
全优96页
全优97页
全优53页能力提高
