6.4.2统计图的选择 课件 (共30张PPT)北师大版数学 七年级上册
文档属性
| 名称 | 6.4.2统计图的选择 课件 (共30张PPT)北师大版数学 七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 13:29:14 | ||
图片预览







文档简介
(共30张PPT)
第六章数据的收集与整理
6.4 统计图的选择
第2课时
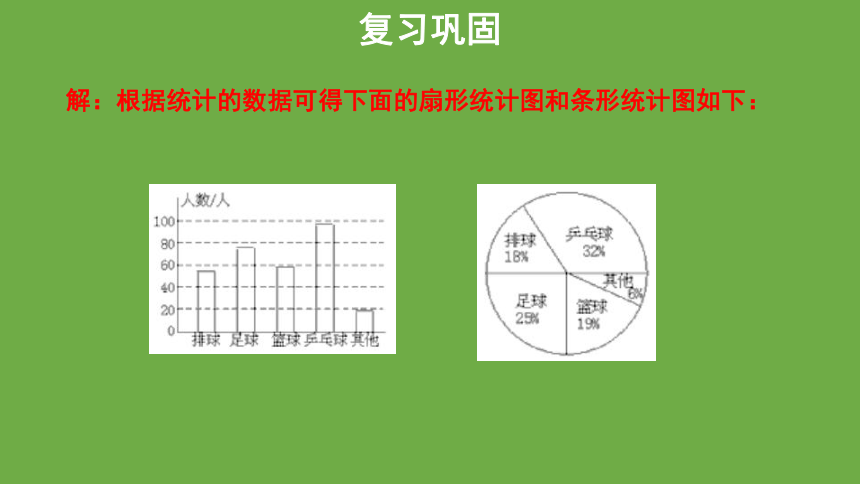
复习巩固
问题:初一年级就“最喜欢的球类运动”曾进行过问卷调查,每人只能报一项,结果300人回答的情况如下表,如何用扇形统计图表示出来.根据图示的信息再制成条形统计图.
排球 54
足球 75
篮球 57
乒乓球 96
其他 18
复习巩固
解:根据统计的数据可得下面的扇形统计图和条形统计图如下:
条形统计图能清楚地表示出每个项目的具体数目;
折线统计图能清楚地反映事物的变化情况;
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
复习巩固
条形统计图的特点;折线统计图的特点;扇形统计图的特点.
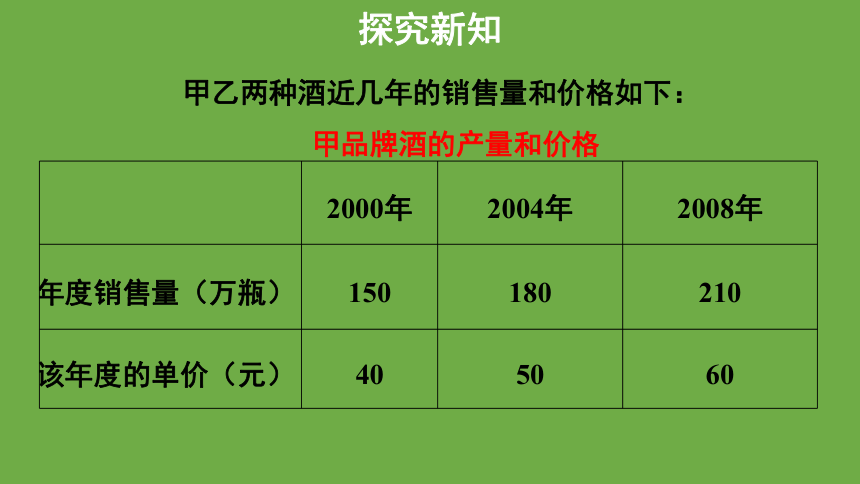
2000年 2004年 2008年
年度销售量(万瓶) 150 180 210
该年度的单价(元) 40 50 60
甲乙两种酒近几年的销售量和价格如下:
甲品牌酒的产量和价格
探究新知
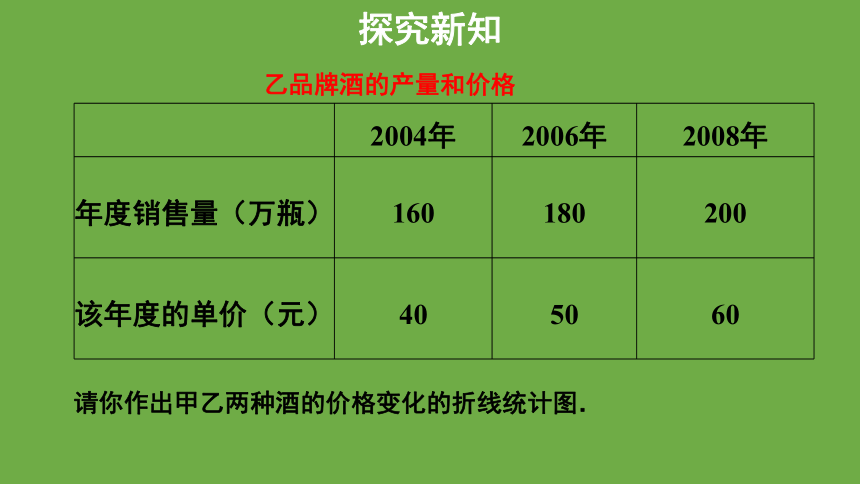
2004年 2006年 2008年
年度销售量(万瓶) 160 180 200
该年度的单价(元) 40 50 60
乙品牌酒的产量和价格
请你作出甲乙两种酒的价格变化的折线统计图.
探究新知
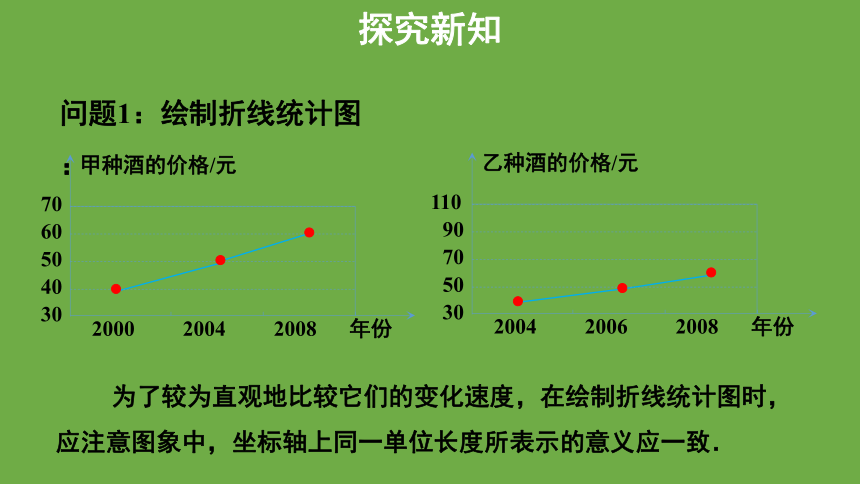
问题1:绘制折线统计图:
为了较为直观地比较它们的变化速度,在绘制折线统计图时,应注意图象中,坐标轴上同一单位长度所表示的意义应一致.
40
50
60
70
2000
2004
2008
甲种酒的价格/元
年份
30
50
70
90
110
2004
2006
2008
乙种酒的价格/元
年份
30
探究新知
思考:为了较直观地比较某两个统计量的变化速度,绘制折线统计图时,应注意什么?
注意把两个统计量的变化绘制在同一个折线统计图中,才能更清晰地比较出这两个统计量的变化速度.
如果绘制在两个折线统计图中,注意统计图横轴、纵轴所选取的单位长度必须一致(特别要注意纵轴的起始数据).
探究新知
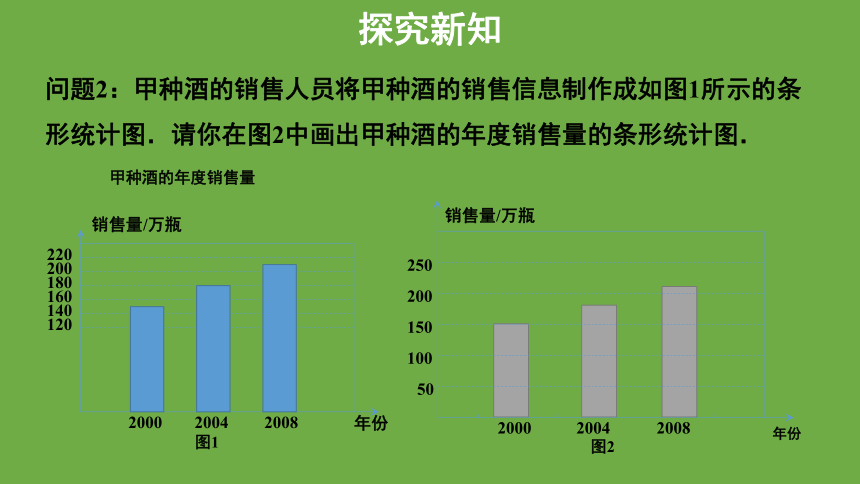
问题2:甲种酒的销售人员将甲种酒的销售信息制作成如图1所示的条形统计图.请你在图2中画出甲种酒的年度销售量的条形统计图.
图2
图1
120
140
160
180
200
220
2000
2004
2008
销售量/万瓶
年份
甲种酒的年度销售量
50
100
150
200
250
2000
2004
2008
销售量/万瓶
年份
探究新知
图1与图2给你的感觉一样吗?在甲种酒销售人员画出的条形统计图中,2008年甲种酒的年度销售量看上去是2000年的多少倍?实际上呢?
根据数据信息,可以计算出在2008年的销售量是2000年的210÷150=1.4倍,但在甲种酒的销售人员自己画的统计图中,感觉上2008年的销售量是2000年的3倍左右,增加得很多.因为人们习惯从“柱”的高度判断多少,而图示的统计图的纵轴不是“0”,下面一段被“砍掉”了,所以会产生3倍的错觉.
探究新知
思考:为了较直观地反映几个统计量之间的比例关系,绘制绘制条形统计图时应注意些什么?
在绘制条形统计图时,纵轴选取单位长度要一致.
探究新知
典型例题
例1 .今年4月,某市国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如图所示的两幅不完整的统计图,请你根据图中所给信息解答下列问题:
(1)请将两幅统计图补充完整;
(2)在这次形体测评中,一共
抽查了________名学生,如果全市
有10万名初中生,那么全市初中生中,
三姿良好的学生约有________人;
(3)根据统计结果,请你简单谈谈自己的看法.
探究新知
分析:本题是一道与抽样调查以及统计图有关的试题,从扇形统计图中可以得到坐姿不良人数占总抽查人数的百分比,从条形统计图中可以观察到坐姿不良的人数是100,联合两个统计图中的信息可以求出抽查的总人数.
典型例题
解:(1)扇形图中填:三姿良好12%,根据条形图可知坐姿不良有100人,根据扇形图可知坐姿不良占抽查人数的20%,所以共抽查了100÷20%=500(人),而站姿不良的人数为500×31%=155,走姿不良的人数为500×37%=185,所以三姿良好有500-100-155-185=60(人),补全的统计图如图所示.
(2)500,12000.
(3)中学生应该坚持锻炼身体,
努力纠正坐姿、站姿、走姿中
的不良习惯,促进身心健康发育.
(答案合理即可)
典型例题
例2 .一所中学准备搬迁到新校舍,在这之前,同学们就该校300名学生如何到校问题进行了一次调查,并得到下列数据:
将上面的数据分别制成扇形统计图和条形统计图,并进行比较,体会它们各自的特点.
步行 60人
骑自行车 100人
坐公共汽车 130人
其他 10人
典型例题
解:根据题意制作下列统计图:
(1)条形统计图(如下图)
(2)扇形统计图(如图)比较这
两个统计图,条形统计图能清楚地
表示出学生到校的几种方式的具体
学生人数;而扇形统计图则清楚地
表示出了学生到校的各种方式在
300名学生中的百分比.
随堂练习
1.(1)为了反映某种股票的涨跌情况,应选择( )
A.扇形统计图 B.折线统计图 C.条形统计图 D.以上都可以
(2)某学校对“大课间活动”中最喜欢的项目进行了一次调查(每个学生只能选一个项目),为了了解各项目学生喜欢的人数比例,得到下表各数据.
则表示这些数据比较适合用( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都不行
项目 跳绳 长跑 篮球 排球 踢毽 其他
所占百分比 24.5% 9.5% 33% 24.6% 6.4% 2%
.B
.A
随堂练习
(3)小明统计一星期用于完成语文、数学、英语、物理和化学作业的时间,列出下表:
宜选择( )统计图进行统计.
A.条形 B.扇形 C.折线 D.条形和折线
科目 语文 数学 英语 物理 化学
时间/时 4 2 3 1.5 1
.A
随堂练习
(4)下列四个统计图,用来表示不同品种的奶牛的平均产奶量最为合适的是( )
B.
C. D.
.
.D
随堂练习
(5)九年级一班同学根据兴趣分成A,B,C,D,E五个小组,把各小组人数分布绘制成如图的不完整的统计图,则D小组的人数
是( )
A.10 B.11 C.12 D.13
C
随堂练习
2 .如图,图中折线表示一辆自行车离家的路程与时间的关系,骑车者九点离开家,十五点到家,根据这个折线图提供的信息,回答下列问题:
(1)到达离家最远的地方是什么时间?离家多远?
(2)他何时开始第一次休息?休息了多长时间?
(3)他在何时至何时停止前进并休息吃午餐?
(4)何时距家22千米?
随堂练习
解:由图可知:
(1)到达离家最远的地方是12点.
(2)这个人10点30分开始第一次休息,他休息了半个小时.
(3)他在12点至13点时休息吃午餐.
(4)11点10分和13点半时距家22千米.
随堂练习
3 .下图是某报社“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题.
(1)本周“百姓热线”共接热线电话
为__________个.
(2)有关道路交通问题的电话
有__________个.
40
200
随堂练习
4 .某校调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
(1)计算出每一种意见的人数是总调查人数的百分之几;
(2)请画出反映此调查结果的条形统计图和扇形统计图;
(3)从统计图中你能得出什么结论?
意见 非常喜欢 喜欢 有点喜欢 不喜欢
人数/人 200 160 32 8
随堂练习
解:(1)“非常喜欢”的人数占总调查人数的: ×100%=50%,
“喜欢”的人数占总调查人数的: ×100%=40%,
“不喜欢”的人数占总调查人数的: ×100%=2%.
随堂练习
(2)如下图:
(3)绝大多数同学喜欢七年级数学实验教材.
(1)哪位同学最高?哪位同学最
矮?他们相差是多少?
(2)舟舟的身高是小丽的几倍?
(3)这个图易使人产生错误的感觉吗?
为什么?
(4)为了更直观、清楚地反映这5名同学的身高状况,这个图应做怎样的改动?
5.小亮根据5名同学的身高绘制了下面的统计图:
随堂练习
解:(1)小亮最高,小丽最矮,相差0.4 m.
(3)这个图易使人产生错误的感觉,如人们从图中易误认为舟舟身高是小丽的3倍.
(4)为了更直观、清楚地反映这5名同学的身高状况,纵轴上的数值应从0开始.
(2)舟舟的身高是小丽的 倍.
随堂练习
1.统计图表直观、形象,便于我们从中得到信息,但有时如果不细心分析,它也会使人们产生“错觉”.
2.为了较直观地比较两个统计量的变化速度,绘制折线统计图时两坐标系的横、纵坐标的单位长度要相应地统一.
3.为了较直观地反映几个统计量之间的比例关系,绘制条形统计图时,纵坐标的起点应设为0.
课堂小结
再见
第六章数据的收集与整理
6.4 统计图的选择
第2课时
复习巩固
问题:初一年级就“最喜欢的球类运动”曾进行过问卷调查,每人只能报一项,结果300人回答的情况如下表,如何用扇形统计图表示出来.根据图示的信息再制成条形统计图.
排球 54
足球 75
篮球 57
乒乓球 96
其他 18
复习巩固
解:根据统计的数据可得下面的扇形统计图和条形统计图如下:
条形统计图能清楚地表示出每个项目的具体数目;
折线统计图能清楚地反映事物的变化情况;
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
复习巩固
条形统计图的特点;折线统计图的特点;扇形统计图的特点.
2000年 2004年 2008年
年度销售量(万瓶) 150 180 210
该年度的单价(元) 40 50 60
甲乙两种酒近几年的销售量和价格如下:
甲品牌酒的产量和价格
探究新知
2004年 2006年 2008年
年度销售量(万瓶) 160 180 200
该年度的单价(元) 40 50 60
乙品牌酒的产量和价格
请你作出甲乙两种酒的价格变化的折线统计图.
探究新知
问题1:绘制折线统计图:
为了较为直观地比较它们的变化速度,在绘制折线统计图时,应注意图象中,坐标轴上同一单位长度所表示的意义应一致.
40
50
60
70
2000
2004
2008
甲种酒的价格/元
年份
30
50
70
90
110
2004
2006
2008
乙种酒的价格/元
年份
30
探究新知
思考:为了较直观地比较某两个统计量的变化速度,绘制折线统计图时,应注意什么?
注意把两个统计量的变化绘制在同一个折线统计图中,才能更清晰地比较出这两个统计量的变化速度.
如果绘制在两个折线统计图中,注意统计图横轴、纵轴所选取的单位长度必须一致(特别要注意纵轴的起始数据).
探究新知
问题2:甲种酒的销售人员将甲种酒的销售信息制作成如图1所示的条形统计图.请你在图2中画出甲种酒的年度销售量的条形统计图.
图2
图1
120
140
160
180
200
220
2000
2004
2008
销售量/万瓶
年份
甲种酒的年度销售量
50
100
150
200
250
2000
2004
2008
销售量/万瓶
年份
探究新知
图1与图2给你的感觉一样吗?在甲种酒销售人员画出的条形统计图中,2008年甲种酒的年度销售量看上去是2000年的多少倍?实际上呢?
根据数据信息,可以计算出在2008年的销售量是2000年的210÷150=1.4倍,但在甲种酒的销售人员自己画的统计图中,感觉上2008年的销售量是2000年的3倍左右,增加得很多.因为人们习惯从“柱”的高度判断多少,而图示的统计图的纵轴不是“0”,下面一段被“砍掉”了,所以会产生3倍的错觉.
探究新知
思考:为了较直观地反映几个统计量之间的比例关系,绘制绘制条形统计图时应注意些什么?
在绘制条形统计图时,纵轴选取单位长度要一致.
探究新知
典型例题
例1 .今年4月,某市国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如图所示的两幅不完整的统计图,请你根据图中所给信息解答下列问题:
(1)请将两幅统计图补充完整;
(2)在这次形体测评中,一共
抽查了________名学生,如果全市
有10万名初中生,那么全市初中生中,
三姿良好的学生约有________人;
(3)根据统计结果,请你简单谈谈自己的看法.
探究新知
分析:本题是一道与抽样调查以及统计图有关的试题,从扇形统计图中可以得到坐姿不良人数占总抽查人数的百分比,从条形统计图中可以观察到坐姿不良的人数是100,联合两个统计图中的信息可以求出抽查的总人数.
典型例题
解:(1)扇形图中填:三姿良好12%,根据条形图可知坐姿不良有100人,根据扇形图可知坐姿不良占抽查人数的20%,所以共抽查了100÷20%=500(人),而站姿不良的人数为500×31%=155,走姿不良的人数为500×37%=185,所以三姿良好有500-100-155-185=60(人),补全的统计图如图所示.
(2)500,12000.
(3)中学生应该坚持锻炼身体,
努力纠正坐姿、站姿、走姿中
的不良习惯,促进身心健康发育.
(答案合理即可)
典型例题
例2 .一所中学准备搬迁到新校舍,在这之前,同学们就该校300名学生如何到校问题进行了一次调查,并得到下列数据:
将上面的数据分别制成扇形统计图和条形统计图,并进行比较,体会它们各自的特点.
步行 60人
骑自行车 100人
坐公共汽车 130人
其他 10人
典型例题
解:根据题意制作下列统计图:
(1)条形统计图(如下图)
(2)扇形统计图(如图)比较这
两个统计图,条形统计图能清楚地
表示出学生到校的几种方式的具体
学生人数;而扇形统计图则清楚地
表示出了学生到校的各种方式在
300名学生中的百分比.
随堂练习
1.(1)为了反映某种股票的涨跌情况,应选择( )
A.扇形统计图 B.折线统计图 C.条形统计图 D.以上都可以
(2)某学校对“大课间活动”中最喜欢的项目进行了一次调查(每个学生只能选一个项目),为了了解各项目学生喜欢的人数比例,得到下表各数据.
则表示这些数据比较适合用( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都不行
项目 跳绳 长跑 篮球 排球 踢毽 其他
所占百分比 24.5% 9.5% 33% 24.6% 6.4% 2%
.B
.A
随堂练习
(3)小明统计一星期用于完成语文、数学、英语、物理和化学作业的时间,列出下表:
宜选择( )统计图进行统计.
A.条形 B.扇形 C.折线 D.条形和折线
科目 语文 数学 英语 物理 化学
时间/时 4 2 3 1.5 1
.A
随堂练习
(4)下列四个统计图,用来表示不同品种的奶牛的平均产奶量最为合适的是( )
B.
C. D.
.
.D
随堂练习
(5)九年级一班同学根据兴趣分成A,B,C,D,E五个小组,把各小组人数分布绘制成如图的不完整的统计图,则D小组的人数
是( )
A.10 B.11 C.12 D.13
C
随堂练习
2 .如图,图中折线表示一辆自行车离家的路程与时间的关系,骑车者九点离开家,十五点到家,根据这个折线图提供的信息,回答下列问题:
(1)到达离家最远的地方是什么时间?离家多远?
(2)他何时开始第一次休息?休息了多长时间?
(3)他在何时至何时停止前进并休息吃午餐?
(4)何时距家22千米?
随堂练习
解:由图可知:
(1)到达离家最远的地方是12点.
(2)这个人10点30分开始第一次休息,他休息了半个小时.
(3)他在12点至13点时休息吃午餐.
(4)11点10分和13点半时距家22千米.
随堂练习
3 .下图是某报社“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题.
(1)本周“百姓热线”共接热线电话
为__________个.
(2)有关道路交通问题的电话
有__________个.
40
200
随堂练习
4 .某校调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
(1)计算出每一种意见的人数是总调查人数的百分之几;
(2)请画出反映此调查结果的条形统计图和扇形统计图;
(3)从统计图中你能得出什么结论?
意见 非常喜欢 喜欢 有点喜欢 不喜欢
人数/人 200 160 32 8
随堂练习
解:(1)“非常喜欢”的人数占总调查人数的: ×100%=50%,
“喜欢”的人数占总调查人数的: ×100%=40%,
“不喜欢”的人数占总调查人数的: ×100%=2%.
随堂练习
(2)如下图:
(3)绝大多数同学喜欢七年级数学实验教材.
(1)哪位同学最高?哪位同学最
矮?他们相差是多少?
(2)舟舟的身高是小丽的几倍?
(3)这个图易使人产生错误的感觉吗?
为什么?
(4)为了更直观、清楚地反映这5名同学的身高状况,这个图应做怎样的改动?
5.小亮根据5名同学的身高绘制了下面的统计图:
随堂练习
解:(1)小亮最高,小丽最矮,相差0.4 m.
(3)这个图易使人产生错误的感觉,如人们从图中易误认为舟舟身高是小丽的3倍.
(4)为了更直观、清楚地反映这5名同学的身高状况,纵轴上的数值应从0开始.
(2)舟舟的身高是小丽的 倍.
随堂练习
1.统计图表直观、形象,便于我们从中得到信息,但有时如果不细心分析,它也会使人们产生“错觉”.
2.为了较直观地比较两个统计量的变化速度,绘制折线统计图时两坐标系的横、纵坐标的单位长度要相应地统一.
3.为了较直观地反映几个统计量之间的比例关系,绘制条形统计图时,纵坐标的起点应设为0.
课堂小结
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
