5.5 应用一元一次方程——“希望工程”义演 课件(共29张PPT) 北师大版数学 七年级上册
文档属性
| 名称 | 5.5 应用一元一次方程——“希望工程”义演 课件(共29张PPT) 北师大版数学 七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 13:31:56 | ||
图片预览








文档简介
(共29张PPT)
第五章一元一次方程
5.5 应用一元一次方程 ——“希望工程”义演
学习目标
1.对于复杂的实际问题,可借助于表格分析数量关系,从而建立方程解决问题;
2.分析题意,选择合适的设未知数.
探究新知
“希望工程”的作用和意义.
某文艺团体为“希望工程”募捐组织了一场义演,共售票1 000张,筹得票款6 950元.
探究新知
(1)说出题目中有哪些已知数量?
它们分别表示什么含义?
探究新知
(2)上面的问题中包含了哪些等量关系?
成人票数+学生票数=1 000张;①
成人票款+学生票款=6 950元.②
探究新知
学生 成人
票数/张 x
票款/元
问题:售出成人票与学生票各多少张?
筹得成人票款与学生票款各多少元?
解法一:设售出的儿童票为x张,填写下表:
探究新知
根据等量关系②,可列出方程
5x+8(1 000-x)=6 950.
解得x=350.
因此售出学生票350张,成人票650张,筹得学生票款1 750元,成人票款5 200元.
探究新知
学生 成人
票数/张
票款/元
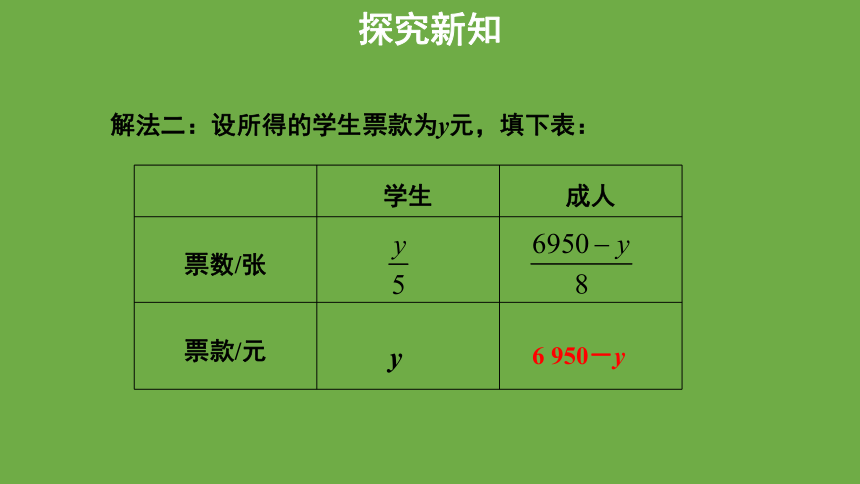
解法二:设所得的学生票款为y元,填下表:
y
6 950-y
探究新知
根据等量关系①,可列出方程
+
解得y=1 750.
因此筹得学生票款1 750元,成人票款5 200元,售出学生票350张,成人票650张.
=1 000.
探究新知
(1)在解决问题的过程中,你遇到了哪些困难,你是如何克服的?
(2)在两种解法中,题目中的两个等量关系分别起了什么作用?
探究新知
(1)在“希望工程”义演的问题中,如果票价不变,那么售出1 000张票所得票款可能是6 930元吗?为什么?
解:假设出售1 000张票所得票款是6 930元,
设售出的学生票为x张,由题意得5x+8(1 000-x)=6 930,
解得x≈356.67.
因为票的张数是整数,所以所得票款不可能是6 930元.
探究新知
(2)在上述问题中,所得票款可能是6 932元吗?如果可能,成人票比学生票多售出多少张?
解:假设出售1 000张票所得票款是6 932元,设售出的学生票为x张,
由题意得5x+8(1 000-x)=6 932,解得x=356.
则:1 000-x=1 000-356=644.
644-356=288.
答:所得票款可能是6 932元.其中成人票比学生票多售出288张.
探究新知
用一元一次方程解决实际问题的一般步骤是什么?
结合框架图,理解此框架图:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
探究新知
例1.初三(1)班举办了一次集邮展览,展出的邮票数若以平均每人3张则多24张,以平均每人4张则少26张,这个班级有多少学生?一共展出了多少张邮票?
学生人数 邮票张数
方案1 x
方案2 x
分析:列表
找出等量关系:邮票总张数相等.
典型例题
解:设这个班有学生x人,
据题意得 3x+24=4x-26.
解得,x=50.
此时,3x+24=150+24=174(张).
答:共有学生50人,邮票174张.
典型例题
例2.某工厂三个车间共有180人,第二车间人数是第一车间人数的3倍还多1人,第三车间人数是第一车间人数的一半还少1人,三个车间各有多少人?
典型例题
解:设第一车间有x人,则第二车间有3(x+1)人,
第三车间有(0.5x-1)人,
据题意得x+3(x+1)+(0.5x-1)=180. 解得 x=40,
此时,3(x+1)= 3(40+1)=121(人),
0.5x-1=0.5×40-1=19(人).
答:第一、二、三车间分别有40人,121人,19人.
典型例题
例3.(1)甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班的人数为x,则可列方程为( ).
A.54+x=2(48-x) B.48+x=2(54-x)
C.54-x=2×48 D.48+x=2×54
A
典型例题
(2)足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分.一个队踢了14场,负了5场,共得
19分,则这个队胜了( ).
A.3场 B.4场
C.5场 D.6场
C
典型例题
(3)一个办公室有5盏灯,其中有40瓦和60瓦的两种,总的瓦数为260瓦,则40瓦的灯有( ).
A.2盏 B.3盏
C.4盏 D.1盏
A
随堂练习
1.(1)苹果的进价是每千克3.8元,销售中估计有5%的苹果正常损
耗,为避免亏本,商家把售价应该至少定为每千克_______元.
(2)刘成买苹果和梨共5千克,用了17元,其中苹果每千克4元,梨每千克3元,那么刘成买了苹果_______千克.
(3)现有面值为2元和5元的人民币共39张,币值共计111元,则面值2元的人民币有________张,面值5元的人民币有________张.
4
2
28
11
随堂练习
2.有甲乙两种学生用本,甲种本的单价是0.25元,乙种本的单价是0.28元,两种本共卖了100本,卖了26.65元,问两种本各卖出多少?
解:设甲种本卖出x个,依题意,得
解这个方程,得 .
所以,100-45=55.
答:卖出甲种本45个,乙种本55个.
随堂练习
3.某城市为了鼓励居民节约用水,对自来水用户按如下标准
收费:若每月每户用水不超过12吨,按每吨1.8元收费;若超过12吨,则超过部分按每吨3.6元收费.如果某户居民某月交水费50.4元,问该户共用了多少吨水?
解:设该户用水x吨,依题意,得 .
解方程,得 .
答:该户共用了20吨水.
随堂练习
4.某车间共有28名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.如果每天生产的螺栓和螺母要按1∶2配套,应分别安排多少工人生产螺栓?多少工人生产螺母?
解:设安排x人生产螺栓,则有(28-x)人生产螺母.
根据题意,得18(28-x)=12x·2,
解这个方程,得x=12,
所以28-x=28-12=16.
答:应安排12人生产螺栓,16人生产螺母才行.
随堂练习
5.某商店售货时,在进价的基础上加上一定利润,其数量与售价的关系如下表,如果数量是x,请根据表中提供的信息,把售价用含有x的代数式表示出来;如果售价
是952.4元,请求出售出该货的数量.
解:由题意可知,售价可以表示
为: ,
当 时, .
即如果售价是952.4元时,
售出该货的数量是119.
数量 售价(元)
1 8+0.4
2 16+0.4
3 24+0.4
4 32+0.4
5 40+0.4
…… ……
6.食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A,B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A,B两种饮料共100瓶,问A,B两种饮料各生产
了多少瓶?
A B
随堂练习
解:设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,依题意,得2x+3(100-x)=270.
解这个方程,得x=30.
于是100-x=70.
答:A饮料生产了30瓶,B饮料生产了70瓶.
随堂练习
课堂小结
1.两个未知量,两个等量关系,如何列方程;
2.寻找中间量;
3.学会用表格分析数量间的关系.
4.遇到较为复杂的实际问题时,我们可以借助表格分析问题中的等量关系,借此列出方程,并进行方程解的检验.
5.同样的一个问题,设未知数的方法不同,所列方程的复杂程度一般也不同,因此在设未知数时要有所选择.
再见
第五章一元一次方程
5.5 应用一元一次方程 ——“希望工程”义演
学习目标
1.对于复杂的实际问题,可借助于表格分析数量关系,从而建立方程解决问题;
2.分析题意,选择合适的设未知数.
探究新知
“希望工程”的作用和意义.
某文艺团体为“希望工程”募捐组织了一场义演,共售票1 000张,筹得票款6 950元.
探究新知
(1)说出题目中有哪些已知数量?
它们分别表示什么含义?
探究新知
(2)上面的问题中包含了哪些等量关系?
成人票数+学生票数=1 000张;①
成人票款+学生票款=6 950元.②
探究新知
学生 成人
票数/张 x
票款/元
问题:售出成人票与学生票各多少张?
筹得成人票款与学生票款各多少元?
解法一:设售出的儿童票为x张,填写下表:
探究新知
根据等量关系②,可列出方程
5x+8(1 000-x)=6 950.
解得x=350.
因此售出学生票350张,成人票650张,筹得学生票款1 750元,成人票款5 200元.
探究新知
学生 成人
票数/张
票款/元
解法二:设所得的学生票款为y元,填下表:
y
6 950-y
探究新知
根据等量关系①,可列出方程
+
解得y=1 750.
因此筹得学生票款1 750元,成人票款5 200元,售出学生票350张,成人票650张.
=1 000.
探究新知
(1)在解决问题的过程中,你遇到了哪些困难,你是如何克服的?
(2)在两种解法中,题目中的两个等量关系分别起了什么作用?
探究新知
(1)在“希望工程”义演的问题中,如果票价不变,那么售出1 000张票所得票款可能是6 930元吗?为什么?
解:假设出售1 000张票所得票款是6 930元,
设售出的学生票为x张,由题意得5x+8(1 000-x)=6 930,
解得x≈356.67.
因为票的张数是整数,所以所得票款不可能是6 930元.
探究新知
(2)在上述问题中,所得票款可能是6 932元吗?如果可能,成人票比学生票多售出多少张?
解:假设出售1 000张票所得票款是6 932元,设售出的学生票为x张,
由题意得5x+8(1 000-x)=6 932,解得x=356.
则:1 000-x=1 000-356=644.
644-356=288.
答:所得票款可能是6 932元.其中成人票比学生票多售出288张.
探究新知
用一元一次方程解决实际问题的一般步骤是什么?
结合框架图,理解此框架图:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
探究新知
例1.初三(1)班举办了一次集邮展览,展出的邮票数若以平均每人3张则多24张,以平均每人4张则少26张,这个班级有多少学生?一共展出了多少张邮票?
学生人数 邮票张数
方案1 x
方案2 x
分析:列表
找出等量关系:邮票总张数相等.
典型例题
解:设这个班有学生x人,
据题意得 3x+24=4x-26.
解得,x=50.
此时,3x+24=150+24=174(张).
答:共有学生50人,邮票174张.
典型例题
例2.某工厂三个车间共有180人,第二车间人数是第一车间人数的3倍还多1人,第三车间人数是第一车间人数的一半还少1人,三个车间各有多少人?
典型例题
解:设第一车间有x人,则第二车间有3(x+1)人,
第三车间有(0.5x-1)人,
据题意得x+3(x+1)+(0.5x-1)=180. 解得 x=40,
此时,3(x+1)= 3(40+1)=121(人),
0.5x-1=0.5×40-1=19(人).
答:第一、二、三车间分别有40人,121人,19人.
典型例题
例3.(1)甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班的人数为x,则可列方程为( ).
A.54+x=2(48-x) B.48+x=2(54-x)
C.54-x=2×48 D.48+x=2×54
A
典型例题
(2)足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分.一个队踢了14场,负了5场,共得
19分,则这个队胜了( ).
A.3场 B.4场
C.5场 D.6场
C
典型例题
(3)一个办公室有5盏灯,其中有40瓦和60瓦的两种,总的瓦数为260瓦,则40瓦的灯有( ).
A.2盏 B.3盏
C.4盏 D.1盏
A
随堂练习
1.(1)苹果的进价是每千克3.8元,销售中估计有5%的苹果正常损
耗,为避免亏本,商家把售价应该至少定为每千克_______元.
(2)刘成买苹果和梨共5千克,用了17元,其中苹果每千克4元,梨每千克3元,那么刘成买了苹果_______千克.
(3)现有面值为2元和5元的人民币共39张,币值共计111元,则面值2元的人民币有________张,面值5元的人民币有________张.
4
2
28
11
随堂练习
2.有甲乙两种学生用本,甲种本的单价是0.25元,乙种本的单价是0.28元,两种本共卖了100本,卖了26.65元,问两种本各卖出多少?
解:设甲种本卖出x个,依题意,得
解这个方程,得 .
所以,100-45=55.
答:卖出甲种本45个,乙种本55个.
随堂练习
3.某城市为了鼓励居民节约用水,对自来水用户按如下标准
收费:若每月每户用水不超过12吨,按每吨1.8元收费;若超过12吨,则超过部分按每吨3.6元收费.如果某户居民某月交水费50.4元,问该户共用了多少吨水?
解:设该户用水x吨,依题意,得 .
解方程,得 .
答:该户共用了20吨水.
随堂练习
4.某车间共有28名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.如果每天生产的螺栓和螺母要按1∶2配套,应分别安排多少工人生产螺栓?多少工人生产螺母?
解:设安排x人生产螺栓,则有(28-x)人生产螺母.
根据题意,得18(28-x)=12x·2,
解这个方程,得x=12,
所以28-x=28-12=16.
答:应安排12人生产螺栓,16人生产螺母才行.
随堂练习
5.某商店售货时,在进价的基础上加上一定利润,其数量与售价的关系如下表,如果数量是x,请根据表中提供的信息,把售价用含有x的代数式表示出来;如果售价
是952.4元,请求出售出该货的数量.
解:由题意可知,售价可以表示
为: ,
当 时, .
即如果售价是952.4元时,
售出该货的数量是119.
数量 售价(元)
1 8+0.4
2 16+0.4
3 24+0.4
4 32+0.4
5 40+0.4
…… ……
6.食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A,B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A,B两种饮料共100瓶,问A,B两种饮料各生产
了多少瓶?
A B
随堂练习
解:设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,依题意,得2x+3(100-x)=270.
解这个方程,得x=30.
于是100-x=70.
答:A饮料生产了30瓶,B饮料生产了70瓶.
随堂练习
课堂小结
1.两个未知量,两个等量关系,如何列方程;
2.寻找中间量;
3.学会用表格分析数量间的关系.
4.遇到较为复杂的实际问题时,我们可以借助表格分析问题中的等量关系,借此列出方程,并进行方程解的检验.
5.同样的一个问题,设未知数的方法不同,所列方程的复杂程度一般也不同,因此在设未知数时要有所选择.
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
