2.1有理数 课件(共26张PPT) 北师大版数学 七年级上册
文档属性
| 名称 | 2.1有理数 课件(共26张PPT) 北师大版数学 七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 13:46:18 | ||
图片预览







文档简介
(共26张PPT)
第二章 有理数及其运算
2.1 有理数
学习目标
1.了解正数与负数是从实际需要中产生的,并会判断一个数是正数还是负数.
2.会用正、负数表示具有相反意义的量.
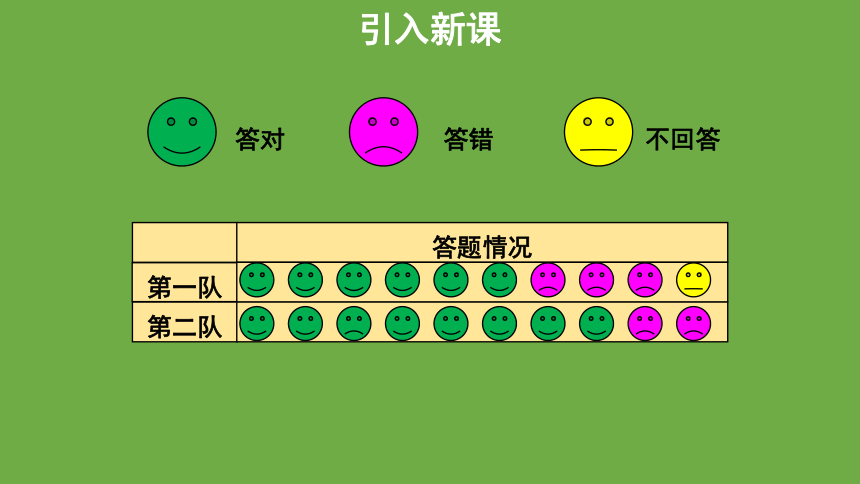
答题情况
第一队
第二队
答对
答错
不回答
引入新课
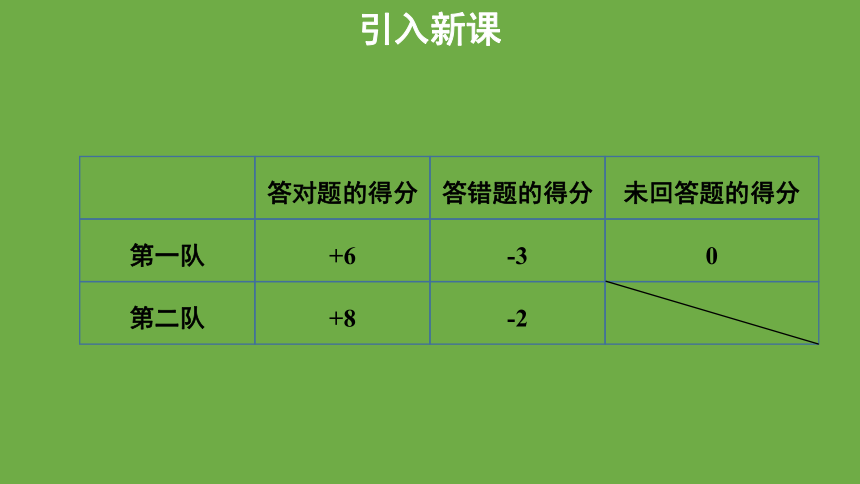
答对题的得分
答错题的得分
未回答题的得分
第一队
+6
-3
0
第二队
+8
-2
引入新课
引入新课
问题1:你能很快地为这两个队排一下名次吗?你的依据是什么?
第二队比较好,因为答对的比较多.
问题2:在完成表格后,你有什么发现?
通过填“答错题的得分”这一栏,发现“-3”“-2”.
常见的温度计
新知讲解
探究新知
2018年1月份居民消费价格同比变化
食品烟酒+3.6%
医疗保健+2.9%
衣着+1.9%
教育文化和娱乐+1.7%
居住+1.4%
交通和通信-1.6%
生活用品及服务+0.6%
其他用品和服务价格-0.4%
新知讲解
正、负数表示现实生活中具有相反意义的量.
像 5,1.2 , …这样的数叫做正数,它们都比0大.
在正数前面加上“-”的数叫做负数,如-10,-3,…
(1)某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?
沿顺时针方向转了12圈记作-12圈.
(2)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02 g记作+0.02 g,那么-0.03 g表示什么?
-0.03 g表示乒乓球的质量低于标准质量0.03 g.
新知讲解
(3)某大米包装袋上标注着“净含量:10 kg±150 g”,这里的“10 kg±150 g”表示什么?
解:每大米的标准质量应为10 kg,但实际每袋大米可能有150 g的误差,即最多超出标准质量150 g,最少少于标准质量150 g.
新知讲解
问题1:在以上3道题中正数、负数分别表示什么量?
问题2:每道题的基准分别是什么?
问题3. 0是正数还是负数?
新知讲解
4.带“-”的数一定是负数吗?
不要认为带“+”的数就是正数,带“-”的数就是负数.如-a不一定是负数.
不是负数
新知讲解
整数和分数统称为有理数.
有理数(按定义)
新知讲解
有理数(按性质)
新知讲解
例1(1)海平面上的高度记为正,海平面下的深度记为负,则海平面下150米记作________;
(2)盈利100元记作+100元,那么亏损100元记作________;
(3)如果零上5 ℃记作+5 ℃,那么零下5 ℃记作________;
-150米
-100元
-5 ℃
典型例题
(4)某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作________;
(5)东西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示______________,物体原地不动记为______;
(6)向南走-4米,实际上是向____走了___米.
-3.8吨
向东运动2米
0米
北
4
典型例题
例2 把下列各数填在相应集合的大括号里:
正数集合{ …}; 负数集合{ …};
整数集合{ …}; 正分数集合{ …};
负分数集合{ …};分数集合{ …}.
12,-3,+1, ,-1.5,0,0.2, , .
典型例题
解:正数集合 ;
负数集合 ;
整数集合 ;
正分数集合 ;
典型例题
负分数集合 ;
分数集合 .
典型例题
1.小学学过的小数是不是有理数?属于分类中的哪一类?
解:有限小数和无限循环小数都是有理数,属于分数;无限不循环小数不是有理数.
随堂练习
2.判断下列说法是否正确:
(1)一个有理数不是整数就是分数;
(2)一个有理数不是正数就是负数;
(3)一个整数不是正整数就是负整数;
(4)一个分数不是正分数就是负分数.
解:第(1)(4)说法正确.
随堂练习
3.一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动±10%.
(1)±10%的含义是什么?
(2)请你算出该商品的最高价格和最低价格;
(3)如果以标准价格为标准,超过标准记作“+”,低于标准记作“-”,该商品价格的浮动范围又可以怎样表示?
随堂练习
解:(1)±10%的含义是在标准的基础上加价或降价的幅度不超过10%.
(2)最高价格为200+200×10%=220(元);最低价格为200-200×10%=180(元).
(3)因为220-200=20(元),200-180=20(元),
所以这件商品加价或降价的幅度不超过20元,
所以这件商品价格的浮动范围又可以表示为±20元.
随堂练习
课堂小结
谈谈我的收获:
1.负数在生活中的应用,及有理数的分类.
2.掌握分类的思想方法.
3.对于有理数的分类理解不是很好,易把两种分类混淆和重复,应通过判断题或选择题的形式多加练习.
1.我们知道了为什么要学习负数,学会了用正、负数表示生活中的具有相反意义的一对量,还知道了有理数都包括哪些数及其分类.
2.我们还要掌握分类的思想方法.
3.学生易困惑的地方:学生对于有理数的分类理解不是很好,易把两种分类混淆和重复,应通过判断题或选择题的形式多加练习.
课堂小结
再见
第二章 有理数及其运算
2.1 有理数
学习目标
1.了解正数与负数是从实际需要中产生的,并会判断一个数是正数还是负数.
2.会用正、负数表示具有相反意义的量.
答题情况
第一队
第二队
答对
答错
不回答
引入新课
答对题的得分
答错题的得分
未回答题的得分
第一队
+6
-3
0
第二队
+8
-2
引入新课
引入新课
问题1:你能很快地为这两个队排一下名次吗?你的依据是什么?
第二队比较好,因为答对的比较多.
问题2:在完成表格后,你有什么发现?
通过填“答错题的得分”这一栏,发现“-3”“-2”.
常见的温度计
新知讲解
探究新知
2018年1月份居民消费价格同比变化
食品烟酒+3.6%
医疗保健+2.9%
衣着+1.9%
教育文化和娱乐+1.7%
居住+1.4%
交通和通信-1.6%
生活用品及服务+0.6%
其他用品和服务价格-0.4%
新知讲解
正、负数表示现实生活中具有相反意义的量.
像 5,1.2 , …这样的数叫做正数,它们都比0大.
在正数前面加上“-”的数叫做负数,如-10,-3,…
(1)某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?
沿顺时针方向转了12圈记作-12圈.
(2)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02 g记作+0.02 g,那么-0.03 g表示什么?
-0.03 g表示乒乓球的质量低于标准质量0.03 g.
新知讲解
(3)某大米包装袋上标注着“净含量:10 kg±150 g”,这里的“10 kg±150 g”表示什么?
解:每大米的标准质量应为10 kg,但实际每袋大米可能有150 g的误差,即最多超出标准质量150 g,最少少于标准质量150 g.
新知讲解
问题1:在以上3道题中正数、负数分别表示什么量?
问题2:每道题的基准分别是什么?
问题3. 0是正数还是负数?
新知讲解
4.带“-”的数一定是负数吗?
不要认为带“+”的数就是正数,带“-”的数就是负数.如-a不一定是负数.
不是负数
新知讲解
整数和分数统称为有理数.
有理数(按定义)
新知讲解
有理数(按性质)
新知讲解
例1(1)海平面上的高度记为正,海平面下的深度记为负,则海平面下150米记作________;
(2)盈利100元记作+100元,那么亏损100元记作________;
(3)如果零上5 ℃记作+5 ℃,那么零下5 ℃记作________;
-150米
-100元
-5 ℃
典型例题
(4)某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作________;
(5)东西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示______________,物体原地不动记为______;
(6)向南走-4米,实际上是向____走了___米.
-3.8吨
向东运动2米
0米
北
4
典型例题
例2 把下列各数填在相应集合的大括号里:
正数集合{ …}; 负数集合{ …};
整数集合{ …}; 正分数集合{ …};
负分数集合{ …};分数集合{ …}.
12,-3,+1, ,-1.5,0,0.2, , .
典型例题
解:正数集合 ;
负数集合 ;
整数集合 ;
正分数集合 ;
典型例题
负分数集合 ;
分数集合 .
典型例题
1.小学学过的小数是不是有理数?属于分类中的哪一类?
解:有限小数和无限循环小数都是有理数,属于分数;无限不循环小数不是有理数.
随堂练习
2.判断下列说法是否正确:
(1)一个有理数不是整数就是分数;
(2)一个有理数不是正数就是负数;
(3)一个整数不是正整数就是负整数;
(4)一个分数不是正分数就是负分数.
解:第(1)(4)说法正确.
随堂练习
3.一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动±10%.
(1)±10%的含义是什么?
(2)请你算出该商品的最高价格和最低价格;
(3)如果以标准价格为标准,超过标准记作“+”,低于标准记作“-”,该商品价格的浮动范围又可以怎样表示?
随堂练习
解:(1)±10%的含义是在标准的基础上加价或降价的幅度不超过10%.
(2)最高价格为200+200×10%=220(元);最低价格为200-200×10%=180(元).
(3)因为220-200=20(元),200-180=20(元),
所以这件商品加价或降价的幅度不超过20元,
所以这件商品价格的浮动范围又可以表示为±20元.
随堂练习
课堂小结
谈谈我的收获:
1.负数在生活中的应用,及有理数的分类.
2.掌握分类的思想方法.
3.对于有理数的分类理解不是很好,易把两种分类混淆和重复,应通过判断题或选择题的形式多加练习.
1.我们知道了为什么要学习负数,学会了用正、负数表示生活中的具有相反意义的一对量,还知道了有理数都包括哪些数及其分类.
2.我们还要掌握分类的思想方法.
3.学生易困惑的地方:学生对于有理数的分类理解不是很好,易把两种分类混淆和重复,应通过判断题或选择题的形式多加练习.
课堂小结
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
