浙江省宁波市部分学校2023-2024学年高一上学期7月入学分班测试数学试卷(Word版含解析)
文档属性
| 名称 | 浙江省宁波市部分学校2023-2024学年高一上学期7月入学分班测试数学试卷(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 08:05:48 | ||
图片预览


文档简介
机密★启用前
宁波市部分学校2023-2024学年高一上学期7月入学分班测试
数学试卷
姓名:___________ 准考证号:___________
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷。试题卷共6页,有四个大题,22个小题。满分为150分,考试时长为120分钟。
2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上。
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满。将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效。
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示。
试 题 卷 Ⅰ
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.平面直角坐标系中,对于不在坐标轴上的点,两点,规定其坐标“积和”运集为:.若,,,四个点的“积和”运算满足:,则以,,,为顶点的四边形不可能是
A.等腰梯形 B.平行四边形 C.矩形 D.菱形
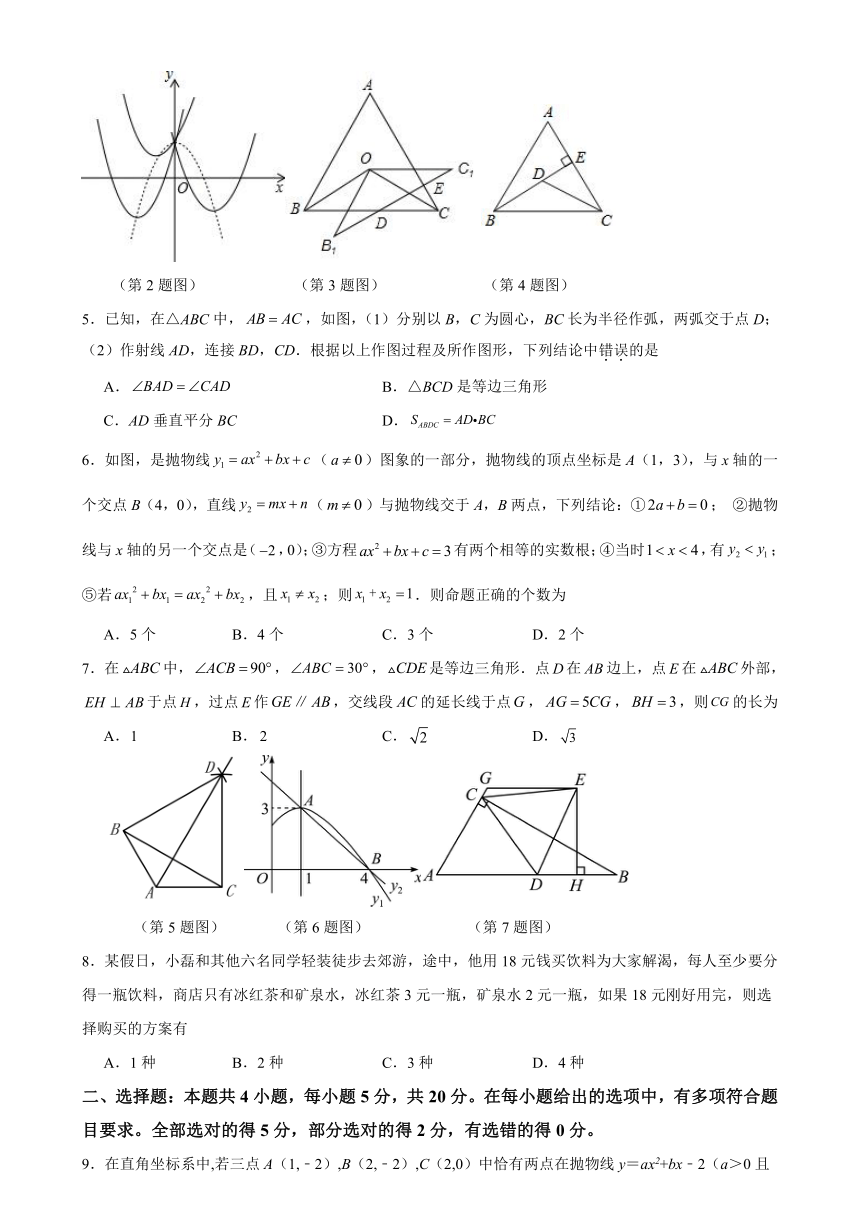
2.已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是
A.y=﹣x2+1 B.y=﹣2x2+1 C.y=﹣x2+1 D.y=﹣4x2+1
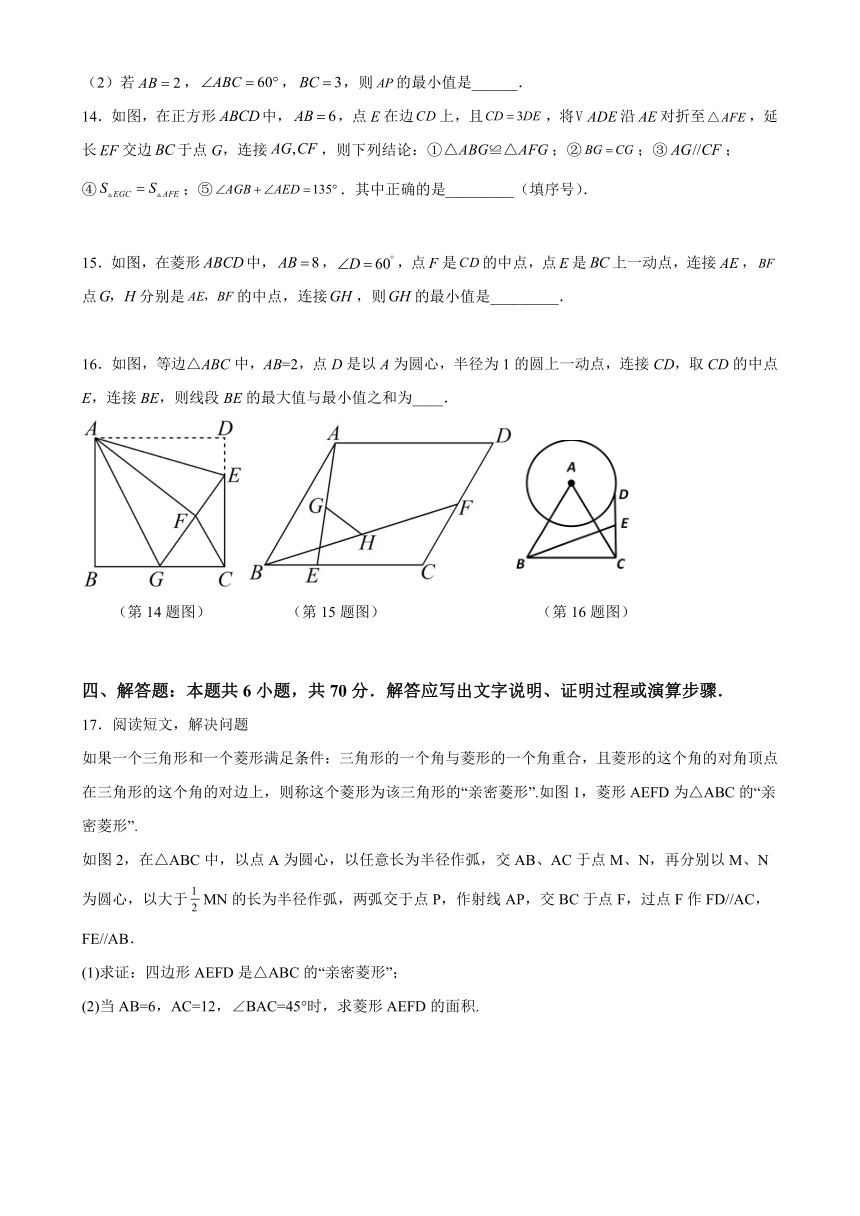
3.如图,点O是边长为2的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则DE的长为
A.2 B. C. D.
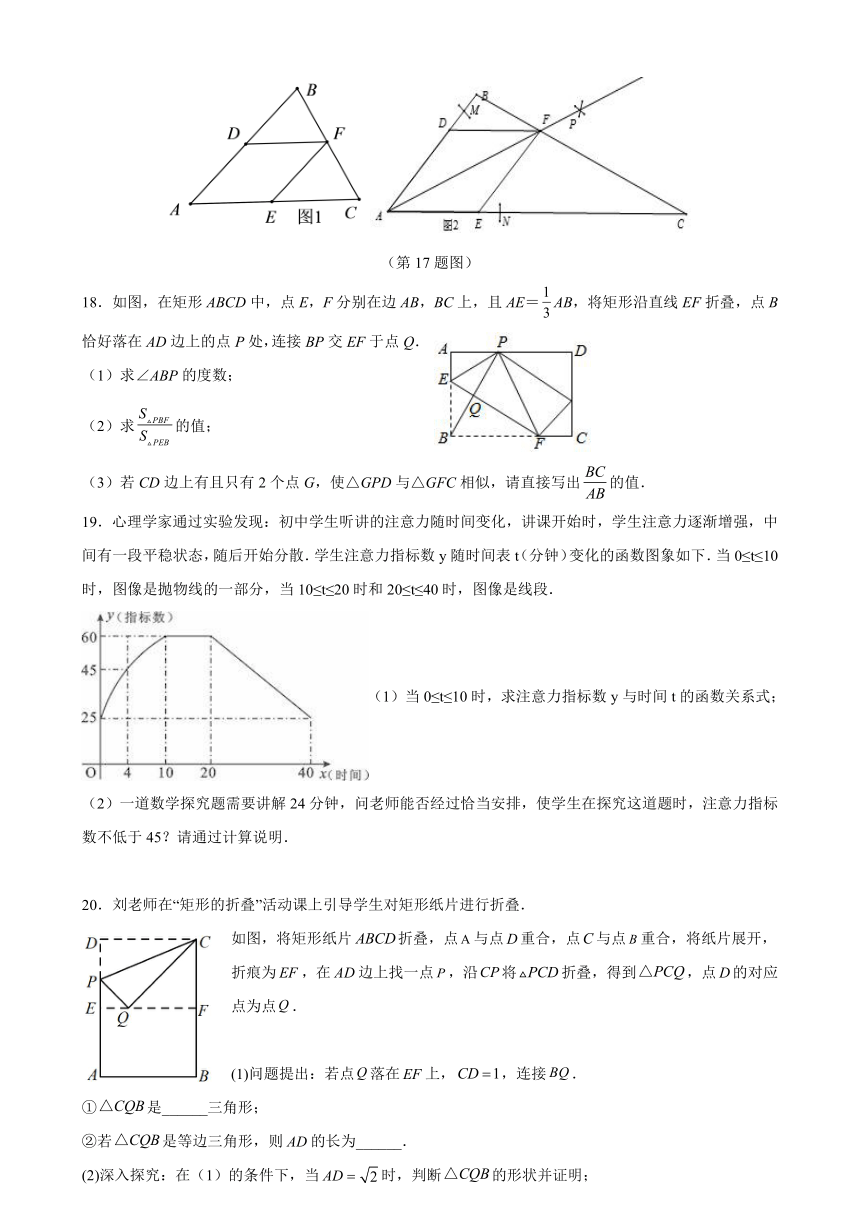
4.如图,中,,于点,,是线段上的一个动点,则的最小值是
A. B. C. D.
(第2题图) (第3题图) (第4题图)
5.已知,在△ABC中,,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是
A. B.△BCD是等边三角形
C.AD垂直平分BC D.
6.如图,是抛物线()图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线()与抛物线交于A,B两点,下列结论:①; ②抛物线与x轴的另一个交点是(,0);③方程有两个相等的实数根;④当时,有;⑤若,且;则.则命题正确的个数为
A.5个 B.4个 C.3个 D.2个
7.在中,,,是等边三角形.点在边上,点在外部,于点,过点作,交线段的延长线于点,,,则的长为
A. B. C. D.
(第5题图) (第6题图) (第7题图)
8.某假日,小磊和其他六名同学轻装徒步去郊游,途中,他用18元钱买饮料为大家解渴,每人至少要分得一瓶饮料,商店只有冰红茶和矿泉水,冰红茶3元一瓶,矿泉水2元一瓶,如果18元刚好用完,则选择购买的方案有
A.1种 B.2种 C.3种 D.4种
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.在直角坐标系中,若三点A(1,﹣2),B(2,﹣2),C(2,0)中恰有两点在抛物线y=ax2+bx﹣2(a>0且a,b均为常数)的图象上,则下列结论正确的是
A.抛物线的对称轴是直线
B.抛物线与x轴的交点坐标是(﹣,0)和(2,0)
C.当t>时,关于x的一元二次方程ax2+bx﹣2=t有两个不相等的实数根
D.若P(m,n)和Q(m+4,h)都是抛物线上的点且n<0,则 .
10.如图,正六边形,点在线段上运动,记图中的面积为,,,,,,已知正六边形边长为2,下列式子的值不随点变化而变化的是
A. B. C. D.
11.若一个平行四边形的四个顶点分别在矩形的四条边上,且一边和矩形的对角线平行,则称这样的平行四边形为该矩形的“反射平行四边形”已知为矩形的“反射平行四边”,点E、F、G、H分别在边、、、上,,设的周长为,和矩形的面积分别为,,则下列结论正确的有
A. B. C. D.
12.如图,正方形的边长为8,点,分别在边,上,将正方形沿折叠,使点落在边上的处,点落在处,交于.下列结论正确的是
A.当为中点时,
B.当时,
C.当(点不与、重合)在上移动时,周长随着位置变化而变化
D.连接,则
(第10题图) (第12题图)
试 题 卷 Ⅱ
三、填空题:本题共4小题,每小题5分,共20分.
13.已知:点是内一点,,与的中垂线交于点,
(1)______°.
(2)若,,,则的最小值是______.
14.如图,在正方形中,,点E在边上,且,将沿对折至,延长交边于点G,连接,则下列结论:①;②;③;④;⑤.其中正确的是_________(填序号).
15.如图,在菱形中,,,点是的中点,点是上一动点,连接,点分别是的中点,连接,则的最小值是_________.
16.如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为____.
(第14题图) (第15题图) (第16题图)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.阅读短文,解决问题
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.
(第17题图)
18.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.
(1)求∠ABP的度数;
(2)求的值;
(3)若CD边上有且只有2个点G,使△GPD与△GFC相似,请直接写出的值.
19.心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图像是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图像是线段.
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
20.刘老师在“矩形的折叠”活动课上引导学生对矩形纸片进行折叠.
如图,将矩形纸片折叠,点与点重合,点与点重合,将纸片展开,折痕为,在边上找一点,沿将折叠,得到,点的对应点为点.
(1)问题提出:若点落在上,,连接.
①是______三角形;
②若是等边三角形,则的长为______.
(2)深入探究:在(1)的条件下,当时,判断的形状并证明;
(3)拓展延伸:若,,其他条件不变,当点落在矩形内部包括边时,连接,直接写出的取值范围.
21.如图①②,和均为直角三角形,,,,点C在边EF的延长线上,,射线EM与AD交于点M,().
(第21题图)
(1)如图①,当点B落在射线EF上时,EM与BA的延长线相交于点G,则______.
(2)如图②,把绕点C逆时针旋转度(),的值是否保持不变?请仅就图②给出你的证明.
(3)若,在绕点C旋转过程中,直接写出线段AD的最大值和最小值.
22.如图,四边形是矩形,点是延长线一点,连接,垂直平分,垂足为,点在上,点在上,且.
(1)若,,求;
(2)若,求证:.
(第22题图)
宁波市部分学校2023-2024学年高一上学期7月入学分班测试数学参考答案及解析
1.D
【分析】根据坐标“积和”运集的计算规则可知A、B、C、D四个点均在反比例函数图象上,据此即可判断结果.
【详解】设、、、,
则有:,,
,,
依据,得,
令,
则可知、、、均在反比例函数上,
根据题意可设构成的四边形为ABCD,则该四边形的对角线为AC和BD,
根据反比例函数图象的特征可知,四个顶点均在双曲线上的四边形的对角线AC与BD无法使得AC⊥BD,故构成的四边形不可能是菱形,
故选:D.
【点睛】本题虽是选择题但构思巧妙,难度较大,主要考查了反比例函数图象特征以及平行四边形、菱形的判定等知识.根据判断、、、均在反比例函数上是解答本题的关键.
2.B
【分析】用含b的式子表示出抛物线的顶点坐标,然后消去b即可得到所求抛物线的解析式.
【详解】解:∵y=2x2+bx+1的顶点坐标是,
设x=,y=,
∴b=﹣4x,
∴y===1﹣2x2.
∴所求抛物线的解析式为:y=1﹣2x2.
故选:B.
【点睛】此题主要考查了二次函数的性质,用含b的式子表示出抛物线的顶点坐标,然后再消去参数b是解题的关键.
3.D
【分析】令与BC的交点为F,与的交点为M,过点F作FN于点N,根据等边三角形的性质及三角形内心的性质,证明△为等腰三角形,继而证明△△,根据相似三角形对应边成比例的性质,解得,再结合△△及解直角三角形求得,由此可解得DE的长.
【详解】令与BC的交点为F,与的交点为M,过点F作FN于点N,如图,
将△OBC绕点O逆时针旋转30°得到△OB1C1,
点O是边长为2的等边△ABC的内心,
△FOB为等腰三角形,
△△
在△和△中
△△
在△中,
故选:D.
【点睛】本题考查三角形的内切圆与内心、旋转的性质、等边三角形的性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.
4.D
【分析】过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,由勾股定理可求BE=4,根据AAS可证△AEB≌△AGC,得CG=BE=4,易证△BDF∽△BAE,得出=,得出DF=,求最小值,即求DF+CD的最小值,由垂线段最短求解即可.
【详解】解:过点D作DF⊥AB于点F,过点C作CG⊥AB于点G
又于点
∴∠AEB=90°,∠DFB=90°,∠AGC=90°
又∠ABE为公共角
∴△BDF∽△BAE
∴=
又,
∴DF=
∴=DF+CD
∵DF+CD≥CG
∴≥CG
即的最小值为CG的长
在Rt△ABE中
BE===4
∵,∠AEB=90°,∠AGC=90°
又∠A为公共角
∴△AEB≌△AGC(AAS)
∴CG=BE=4
∴的最小值为4
故选:D
【点睛】本题主要考查最短路径中的垂线段最短问题,解决本题借助了全等三角形的判定和性质,等腰三角形的性质,相似三角形以及勾股定理求边长,综合性较强,难度较大.
5.D
【分析】根据作图过程及所作图形可知,得出△BCD是等边三角形;又因为,,推出,继而得出;根据,,可知AD为的角平分线,根据三线合一得出AD垂直平分BC;
四边形ABCD的面积等于的面积与的面积之和,为.
【详解】解:∵
∴△BCD是等边三角形
故选项B正确;
∵,
∴
∴
故选项A正确;
∵,
∴据三线合一得出AD垂直平分BC
故选项C正确;
∵四边形ABCD的面积等于的面积与的面积之和
∴
故选项D错误.
故选:D.
【点睛】本题考查的知识点是等边三角形的判定、全等三角形的判定及性质、线段垂直平分线的判定以及四边形的面积,考查的范围较广,但难度不大.
6.B
【分析】先利用待定系数法求出抛物线解析式,和一次函数解析式,根据抛物线对称轴可判断①,利用抛物线的对称轴与x轴的一个交点可求另一交点可判断②,利用抛物线平移和顶点的位置可判断③,利用二次函数图像与一次函数的图象的位置比较大小,可判断④,根据可得出y1=y2,利用对称性与对称轴关系可判断⑤即可.
【详解】解:∵抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),
∴,
把B点坐标代入得,
解得,
抛物线,
直线()与抛物线交于A,B两点,
∴,
解得,
直线,
①∵对称轴为,则
故①正确;
②∵对称轴为直线,与轴的一个交点是,设另一交点为(m,0),
∴1-m=4-1,
∴m=-2,
与轴的另一个交点是,故②正确;
③∵把抛物线向下平移3个单位,得到,
∴顶点坐标变为,即抛物线与只有一个交点,
∴方程有两个相等的实数根,故③正确;
④当时,二次函数图像在一次函数图像的上方
∴,故④正确;
⑤若,即
即,
则关于函数的对称轴对称,
故,即,故⑤错误,
∴命题正确的有①②③④四个.
故选:B.
【点睛】本题考查了抛物线与的交点,以及函数图象上点的坐标特征,要求学生熟练掌握函数与坐标轴的交点,顶点等点坐标的求法以及这些点代表的意义及函数特征.
7.B
【分析】取的中点,连接、、,根据题意得出和全等,然后得出和全等,设,则,,根据题意列出一元一次方程求出的值得出答案.
【详解】取的中点,连接、、,
,,
,,
为等边三角形,
,
是等边三角形,
,
,
,
,
∵
,
,
,
,
,
,
,
∵为等边三角形,
∴,
∴,
∵是等边三角形,
∴,
设,则,
,
∴
在和中,
,
,
设,则,,
,
,
,
解得,,
即.
故选:B.
【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,平行线的性质,熟练掌握是解题的关键.
8.C
【分析】本题的等量关系为:冰红茶总价钱+矿泉水总价钱=18,冰红茶瓶数+矿泉水瓶数≥7,然后整理求非负整数解即可.
【详解】解:设买冰红茶x瓶、矿泉水y瓶,
根据题意得 ,(且x、y均为非负整数)
则,
所以有3种购买方式,故选C.
【点睛】本题主要考查了二元一次方程的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系,讨论出符合条件的整数解.
9.ACD
【分析】利用待定系数法将各点坐标两两组合代入,求得抛物线解析式为 ,再根据对称轴直线 求解即可得到A选项是正确答案,由抛物线解析式为,令 ,求解即可得到抛物线与x轴的交点坐标(-1,0)和(2,0),从而判断出B选项不正确,令关于x的一元二次方程 的根的判别式当,解得 ,从而得到C选项正确,根据抛物线图象的性质由 ,推出 ,从而推出 ,得到D选项正确.
【详解】当抛物线图象经过点A和点B时,将A(1,-2)和B(2,-2)分别代入,
得,解得 ,不符合题意,
当抛物线图象经过点B和点C时,将B(2,-2)和C(2,0)分别代入,
得,此时无解,
当抛物线图象经过点A和点C时,将A(1,-2)和C(2,0)分别代入得,解得,因此,抛物线经过点A和点C,其解析式为,抛物线的对称轴为直线 ,故A选项正确,
因为,所以 ,抛物线与x轴的交点坐标是(-1,0)和(2,0),故B选项不正确,
由得,方程根的判别式 当 , 时, ,当时,即,解得 ,此时关于x的一元二次方程有两个不相等的实数根,故C选项正确,
因为抛物线与x轴交于点(-1,0)和(2,0),且其图象开口向上,若P(m,n)和Q(m+4,h)都是抛物线上的点,且n<0,得 ,又得 ,
所以h>0,故D选项正确.
故选ACD.
【点睛】本题考查抛物线与x轴的交点 根的判别式 二次函数的性质及二次函数图象上点的坐标特征,解题的关键是利用数形结合思想,充分掌握求二次函数的对称轴及交点坐标的解答方法.
10.BD
【分析】连接,,,,交于,在正六边形中求得,推得,易得,,,设,则,分别求得计算即可.
【详解】解:连接,,,,交于,
∵六边形为正六边形,
∴,,
∴,
∴,,,
∴四边形是矩形,
在中,,∴,
故
∴,,
∵,,
∴
则,,
∴,
设,则,
∴,
,
,
,
,
,
故;
;
;
;
故选:BD.
【点睛】本题考查了正多边形的性质,等腰三角形的性质,勾股定理,三角形面积公式,矩形的判定和性质,角所对的直角边等于斜边的一半等,熟练掌握正多边形的性质是解题的关键.
11.BCD
【分析】延长,交于点,根据平行四边形的性质,矩形的性质,以及平行线分线段成比例,逐一进行判断即可.
【详解】如图,延长,交于点,
在平行四边形中,,
,
,与不一定相等,
不一定成立,
即不一定相等,故A选项不符合题意;
在矩形中,
,,
,
在平行四边形中,
,
,
,
,
,
,,
,
,故B选项正确;
,,
,,
在矩形中,
,
,故C选项正确;
点为中点,,
点为中点,同理可得点为中点,
∴,,
设,则,
,,
,
,
,故D选项正确.
故选BCD.
【点睛】本题考查平行四边形的性质,矩形的性质,平行线分线段成比例,配方法的应用.熟练掌握相关性质,并灵活运用,根据题意正确的画出图形,利用数形结合的思想进行求解,是解题的关键.
12.ABD
【分析】当为CD中点时,设则,由勾股定理列方程求解,进一步求得的值,进而可判断A的正误;当三边之比为3:4:5时,设,,,由可求a 的值,进一步求得的值,进而可判断B的正误;过点A作,垂足为H,连接,AG,先证,可得,,再证,可得,由此证得周长=16,进而可判断C的正误;过点E作EM⊥BC,垂足为M,连接交EM,EF于点N,Q,证明,进而可判断D的正误.
【详解】:∵为CD中点,正方形ABCD的边长为8,
∴,
由折叠的性质,设则,
在中,由勾股定理得,即42+(8﹣x)2=x2,
解得x=5,
∴AE=5,DE=3,
∴,
故A正确;
当三边之比为3:4:5时,设,,,则,
∵,
∴,
解得:,
∴,,
故B正确;
过点A作,垂足为H,连接,AG,则,
由折叠的性质可知,
∴,
∵,
∴,
∵,
∴,
∴,
在和中
,
∴,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∴周长
,
∴当在CD上移动时,周长不变,
故C错误;
如图,过点E作EM⊥BC,垂足为M,连接交EM,EF于点N,Q,
∴,,
∴,
由翻折可知:EF垂直平分,
∴,
∴,
∴,
在和中,
,
,
∴,
故D正确.
故选:ABD.
【点睛】本题考查了正方形的性质,折叠的性质,勾股定理,全等三角形的判定与性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.
13. 90
【分析】(1)设,画出图形,由得,由得,由得,再利用三角形内角和定理得到答案;
(2)求出是定值,点P在以M为圆心,长为半径的圆上,连接,交圆M于点,得到,过点M作,根据三角函数求出,,由勾股定理求出连接,则,当P与重合时,有最小值,求出即可.
【详解】解:(1)设,如图,
则,
由题意可得,M是和中垂线上的点,
∴即,
∵,
∴,
∵,
∴,
又,
∴,
∵,
∴,
∴,
又,,
在中,有,
∴,
即,
即;
故答案为:90
(2)如图,
∵,
∴,即,
在中,,
∵是定值,
∴是定值,
即点P在以M为圆心,长为半径的圆上,
连接,交圆M于点,
由(1)中结论可知,又,
∴,
又,
∴,
过点M作,
∵,
∴,
∵,
∴,即,
∴,即,
又,
∴,
连接,则,
当P与重合时,有最小值,
∵,即,即
∴,即最小值为
综上,最小值为,
故答案为:.
【点睛】此题考查了线段垂直平分线的性质,三角形内角和定理,锐角三角函数,动点问题,勾股定理,正确作出辅助线及掌握各知识点是解题的关键.
14.①②③④⑤
【分析】根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG//CF;分别求出S△EGC与S△AFE的面积比较即可;求得∠GAF=45°,∠AGB+∠AED=180°-∠GAF=135°,即可得到答案.
【详解】解:∵AB=AD=AF,AG=AG,∠B=∠AFG = 90°,
∴,
故①正确;
∵,
∴,
∴,
设,则,
在中,由勾股定理得:,
即:,
解得:,
∴,
∴,
故②正确;
∵,
∴,
∵是等腰三角形,,
∵Rt△ABG≌Rt△AFG,
∴,
∴,
∴,
∴,
故③正确;
∵,,
∴,
故④正确;
∵,
又∵,
∴,
∴,
故⑤正确;
故答案为:①②③④⑤.
【点睛】本题考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想与方程思想的应用.
15.
【分析】连接交于点,连接易证得,得到点G为的中点,所以是中位线,可得到,求最小值即为求最小值的一半,随着点E的变化,点M在上动,即当时,有最小值,然后在中,借助三角函数计算即可.
【详解】解:如图,连接交于点,连接,过点作于点N,
∵点为中点,
∴,
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴点G为的中点,
∵点H为的中点,
∴是中位线,
∴,
∴求最小值即为求最小值的一半,随着点E的变化,点M在上动,即当时,有最小值,即最小值=,
∵是的中点,
∴,
∵
∴,
∴.
故答案为:
【点睛】本题主要考查动点最值,根据条件做出辅助线,利用中位线转化所求线段,然后借助点到线距离垂线段最短计算即可.
16.
【分析】取点D的特殊位置:当点D与点F重合时,当点D在CA延长线与圆A的交点时,当CD与圆A相切时,确定FE的长度都是0.5,从而得到点E的运动轨迹是以点F为圆心,0.5为半径的圆上运动,故而得到线段BE的最大值与最小值,由此得到答案.
【详解】∵△ABC为等边三角形,AB=2,
∴AC=AB=2,
设AC交圆A于点F,
∵点D是以A为圆心,半径为1的圆上一动点,
∴当点D与点F重合时,如图1,FE=0.5,
当点D在CA延长线与圆A的交点时,如图2,FE=0.5,
当CD与圆A相切时,FE=0.5,
故点E在以点F为圆心,0.5为半径的圆上运动,
当点B、F、E三点共线时,线段BE有最大值和最小值,如图4:
∵AF=1,AC=2,
∴FC=1,
∴点F是AC的中点,
∵△ABC是等边三角形,
∴BF⊥AC,
∴BF= ,
线段BE的最大值=,最小值=,
∴线段BE的最大值与最小值之和为,
故答案为:.
【点睛】此题考查圆与动点问题,圆的性质,圆的切线的性质定理,等边三角形的性质,勾股定理,根据题意理解点D运动的路线得到点E的运动轨迹是解题的关键.
17.(1)证明见解析;(2) 四边形的面积为.
【详解】【分析】(1)根据尺规作图可知AF平分∠BAC,再根据DF//AC,可得AD=DF,再由两组对边分别平行的四边形是平行四边形可得四边形AEFD是平行四边形,继而可得平行四边形AEFD是菱形,根据“亲密菱形”的定义即可得证;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,可证得△BDF∽△BAC,根据相似三角形的性质可求得a=4,过D作DG⊥AC,垂足为G,在Rt△ADG中, DG=2,继而可求得面积.
【详解】(1)由尺规作图可知AF平分∠BAC,
∴∠DAF=∠EAF,
∵DF//AC,∴∠DFA=∠EAF,∴∠DAF=∠DFA,∴AD=DF,
∵FD//AC,FE//AB,∴四边形AEFD是平行四边形,
∴平行四边形AEFD是菱形,
∵∠BAC与∠DAE重合,点F点BC上,
∴菱形AEFD为△ABC的“亲密菱形”;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,
∵DF//AC,∴△BDF∽△BAC,
∴BD:BA=BF:AC,
即(6-a):6=a:12,
∴a=4,
过D作DG⊥AC,垂足为G,
在Rt△ADG中,∠DAG=45°,∴DG=AD=2,
∴S菱形AEFD=AE DG=8,
即四边形AEFD的面积为8.
【点睛】本题考查了尺规作图,新概念题,菱形的判定与性质等,正确理解新概念是解题的关键.
18.(1)∠ABP=30°;(2)3;(3)
【分析】(1)证明,推出即可解决问题.
(2)由翻折可知:EF垂直平分PB,设,求出即可解决问题.
(3)如图3﹣1中,作点P关于CD的对称点N,连接FN交CD于G,此时 ,以PF为直径作圆交CD 于,此时 ,.①当点G与G2重合时,满足条件,易证 ,设.构建方程求出a与b的关系即可解决问题.②当G1,与G2重合时,满足条件,此时以PF为直径的圆与CD相切,设,构建方程求出m与n的关系即可解决问题.
【详解】解:(1)∵ ,
∴,
由翻折可知:,
∴ ,
∵四边形ABCD是矩形,
∴,
∴,
∴,
∵ ,
∴ ,
∴.
(2)由翻折可知:EF垂直平分PB,设,
在中,∵ ,
∴,
在中, ,
∴ ,
∴ ,
∴ ,
∴ .
(3)如图3﹣1中,作点P关于CD的对称点N,连接FN交CD于G,此时,以PF为直径作圆交CD 于G1,G2,此时 ,.
①当点G与G2重合时,满足条件,易证,设 ,
则: ,
∵ ,
∴ ,
∴ ,
∴ .
②当G1,与G2重合时,满足条件,此时以PF为直径的圆与CD相切,设 ,
则:, ,
∵,
∴ ,
∴,
∴,,
∴ .
【点睛】本题属于相似三角形综合题,考查了相似三角形的判定和性质,解题的关键是学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
19.(1);(2)能,理由见解析.
【详解】试题分析:(1)直接利用待定系数法求二次函数解析式进而得出答案;
(2)首先利用待定系数法求出一次函数解析式,进而令y=45,有45=-x+95,求出x的值,进而得出讲课后注意力不低于45的时间.
(1)当0≤t≤10时,设抛物线的函数关系式为y=ax2+bx+c.由于它的图象经过点(0,25),(4,45),(10,60),
所以,
解得:,
所以;
(2)当20≤x≤40时,设函数解析式为:y=kx+d,将(20,60),(40,25)代入得:
,
解得:
∴,
令y=45,有45=-x+95,
解得:x=,
即讲课后第分钟时注意力不低于45,
当0≤x≤10时,令y=45,有45=-x2+6x+25,
解得:x1=4,x2=20(舍去),
即讲课后第4分钟时,注意力不低于45,
所以讲课后注意力不低于45的时间有(分钟)>24(分钟),
所以老师可以经过适当的安排,使学生在探究这道数学题时,注意力指数不低于45.
考点:二次函数的应用.
20.(1)①等腰;②1
(2)是等腰直角三角形,证明见解析
(3)的取值范围是
【分析】(1)①根据折叠的性质得出垂直平分,根据垂直平分线的性质即可得出是等腰三角形;
②由折叠得,若是等边三角形,则,根据矩形的性质得出,
(2)由得,根据勾股定理的逆定理得出,证明是直角三角形,进而即可得出结论;
(3)连接,以点为圆心,长为半径作圆交于点,交于点,得出,即点在上运动,连接、、,则,当点落在矩形内部包括边时,则.
【详解】(1)如图1,①将矩形纸片沿折叠,点与点重合,
垂直平分,
,
是等腰三角形,
故答案为:等腰.
②由折叠得,
若是等边三角形,则,
四边形是矩形,
,
故答案为:.
(2)是等腰直角三角形,
证明:如图,由得,
∴,
∵,
∴
∴,
是直角三角形,
,
是等腰直角三角形.
(3)如图,连接,以点为圆心,长为半径作圆交于点,交于点,
,,,
,
,
点在上运动,
连接、、,则,
,
四边形是矩形,
,,
,
,
当点落在矩形内部包括边时,则,
即,
∴的取值范围是.
【点睛】本题考查了矩形与折叠问题,等腰三角形的性质与判定,等边三角形的性质与判定,勾股定理,圆外一点到圆的最值问题,轴对称的性质,综合运用以上知识是解题的关键.
21.(1)
(2)保持不变,见解析
(3)线段AD的最大值为,最小值为
【分析】(1)在Rt△DEF中,根据,,求出,在Rt△ABC中,根据,,求出,在Rt△GEB中,根据,,求出,算出AG,证明,得出即可;
(2)过B点作,交射线EM于点G,连接AG,根据,,证明,得出,,证明,得,进而得出即可;
(3)由题意得,点A在以C为圆心,以CA为半径的圆上移动,当点D、A、C三点共线时,是最小值,是最大值,然后求出DC、AC即可得出答案.
(1)
解:∵在Rt△DEF中,,,
∴,
∵在Rt△ABC中,,,
∴,
,
∴,
∵在Rt△GEB中,
∴
∴,
,
∴,
∴.
故答案为:.
(2)
保持不变.理由如下:
过B点作,交射线EM于点G,连接AG,
∵,
∴,,
∵在中,,
∴,,
∴,,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴;
(3)
由题意得,点A在以C为圆心,以CA为半径的圆上移动,如图所示:
∴当点D、A、C三点共线时,是最小值,是最大值,
∵在中,,,
∴,
∵在Rt△ABC中,,,
∴,
∴线段AD的最大值为,最小值为.
【点睛】本题主要考查了解直角三角形,特殊角的三角函数值,勾股定理,三角形相似的判定和性质,平行线的判定和性质,根据题意得出点A在以C为圆心,以CA为半径的圆上移动,当点D、A、C三点共线时,是最小值,是最大值,是解决问题的关键.
22.(1)
(2)见解析
【分析】(1)由垂直平分线的性质可得,由勾股定理可求,的长,即可求解;
(2)在上截取,在上截取,连接.由“”可得,可得,,可证,通过证明,可得,结合题意即可得出,进而得出,最后由三角形中位线的性质即可得出结论.
【详解】(1)解:如图,连接,
,,
.
垂直平分,
∴,,
∴,
∴,
∴;
(2)证明:如图,在上截取,在上截取,连接.
在和中,,
∴,
∴,,,
∴.
又∵,
∴,
,
.
,,
,
,
,
,
,
.
【点睛】本题考查矩形的性质,勾股定理,线段垂直平分线的性质,相似三角形的判定和性质,全等三角形的判定和性质等知识,添加恰当辅助线构造全等三角形是解题的关键.
宁波市部分学校2023-2024学年高一上学期7月入学分班测试
数学试卷
姓名:___________ 准考证号:___________
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷。试题卷共6页,有四个大题,22个小题。满分为150分,考试时长为120分钟。
2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上。
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满。将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效。
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示。
试 题 卷 Ⅰ
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.平面直角坐标系中,对于不在坐标轴上的点,两点,规定其坐标“积和”运集为:.若,,,四个点的“积和”运算满足:,则以,,,为顶点的四边形不可能是
A.等腰梯形 B.平行四边形 C.矩形 D.菱形
2.已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是
A.y=﹣x2+1 B.y=﹣2x2+1 C.y=﹣x2+1 D.y=﹣4x2+1
3.如图,点O是边长为2的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则DE的长为
A.2 B. C. D.
4.如图,中,,于点,,是线段上的一个动点,则的最小值是
A. B. C. D.
(第2题图) (第3题图) (第4题图)
5.已知,在△ABC中,,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是
A. B.△BCD是等边三角形
C.AD垂直平分BC D.
6.如图,是抛物线()图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线()与抛物线交于A,B两点,下列结论:①; ②抛物线与x轴的另一个交点是(,0);③方程有两个相等的实数根;④当时,有;⑤若,且;则.则命题正确的个数为
A.5个 B.4个 C.3个 D.2个
7.在中,,,是等边三角形.点在边上,点在外部,于点,过点作,交线段的延长线于点,,,则的长为
A. B. C. D.
(第5题图) (第6题图) (第7题图)
8.某假日,小磊和其他六名同学轻装徒步去郊游,途中,他用18元钱买饮料为大家解渴,每人至少要分得一瓶饮料,商店只有冰红茶和矿泉水,冰红茶3元一瓶,矿泉水2元一瓶,如果18元刚好用完,则选择购买的方案有
A.1种 B.2种 C.3种 D.4种
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.在直角坐标系中,若三点A(1,﹣2),B(2,﹣2),C(2,0)中恰有两点在抛物线y=ax2+bx﹣2(a>0且a,b均为常数)的图象上,则下列结论正确的是
A.抛物线的对称轴是直线
B.抛物线与x轴的交点坐标是(﹣,0)和(2,0)
C.当t>时,关于x的一元二次方程ax2+bx﹣2=t有两个不相等的实数根
D.若P(m,n)和Q(m+4,h)都是抛物线上的点且n<0,则 .
10.如图,正六边形,点在线段上运动,记图中的面积为,,,,,,已知正六边形边长为2,下列式子的值不随点变化而变化的是
A. B. C. D.
11.若一个平行四边形的四个顶点分别在矩形的四条边上,且一边和矩形的对角线平行,则称这样的平行四边形为该矩形的“反射平行四边形”已知为矩形的“反射平行四边”,点E、F、G、H分别在边、、、上,,设的周长为,和矩形的面积分别为,,则下列结论正确的有
A. B. C. D.
12.如图,正方形的边长为8,点,分别在边,上,将正方形沿折叠,使点落在边上的处,点落在处,交于.下列结论正确的是
A.当为中点时,
B.当时,
C.当(点不与、重合)在上移动时,周长随着位置变化而变化
D.连接,则
(第10题图) (第12题图)
试 题 卷 Ⅱ
三、填空题:本题共4小题,每小题5分,共20分.
13.已知:点是内一点,,与的中垂线交于点,
(1)______°.
(2)若,,,则的最小值是______.
14.如图,在正方形中,,点E在边上,且,将沿对折至,延长交边于点G,连接,则下列结论:①;②;③;④;⑤.其中正确的是_________(填序号).
15.如图,在菱形中,,,点是的中点,点是上一动点,连接,点分别是的中点,连接,则的最小值是_________.
16.如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为____.
(第14题图) (第15题图) (第16题图)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.阅读短文,解决问题
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.
(第17题图)
18.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.
(1)求∠ABP的度数;
(2)求的值;
(3)若CD边上有且只有2个点G,使△GPD与△GFC相似,请直接写出的值.
19.心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图像是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图像是线段.
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
20.刘老师在“矩形的折叠”活动课上引导学生对矩形纸片进行折叠.
如图,将矩形纸片折叠,点与点重合,点与点重合,将纸片展开,折痕为,在边上找一点,沿将折叠,得到,点的对应点为点.
(1)问题提出:若点落在上,,连接.
①是______三角形;
②若是等边三角形,则的长为______.
(2)深入探究:在(1)的条件下,当时,判断的形状并证明;
(3)拓展延伸:若,,其他条件不变,当点落在矩形内部包括边时,连接,直接写出的取值范围.
21.如图①②,和均为直角三角形,,,,点C在边EF的延长线上,,射线EM与AD交于点M,().
(第21题图)
(1)如图①,当点B落在射线EF上时,EM与BA的延长线相交于点G,则______.
(2)如图②,把绕点C逆时针旋转度(),的值是否保持不变?请仅就图②给出你的证明.
(3)若,在绕点C旋转过程中,直接写出线段AD的最大值和最小值.
22.如图,四边形是矩形,点是延长线一点,连接,垂直平分,垂足为,点在上,点在上,且.
(1)若,,求;
(2)若,求证:.
(第22题图)
宁波市部分学校2023-2024学年高一上学期7月入学分班测试数学参考答案及解析
1.D
【分析】根据坐标“积和”运集的计算规则可知A、B、C、D四个点均在反比例函数图象上,据此即可判断结果.
【详解】设、、、,
则有:,,
,,
依据,得,
令,
则可知、、、均在反比例函数上,
根据题意可设构成的四边形为ABCD,则该四边形的对角线为AC和BD,
根据反比例函数图象的特征可知,四个顶点均在双曲线上的四边形的对角线AC与BD无法使得AC⊥BD,故构成的四边形不可能是菱形,
故选:D.
【点睛】本题虽是选择题但构思巧妙,难度较大,主要考查了反比例函数图象特征以及平行四边形、菱形的判定等知识.根据判断、、、均在反比例函数上是解答本题的关键.
2.B
【分析】用含b的式子表示出抛物线的顶点坐标,然后消去b即可得到所求抛物线的解析式.
【详解】解:∵y=2x2+bx+1的顶点坐标是,
设x=,y=,
∴b=﹣4x,
∴y===1﹣2x2.
∴所求抛物线的解析式为:y=1﹣2x2.
故选:B.
【点睛】此题主要考查了二次函数的性质,用含b的式子表示出抛物线的顶点坐标,然后再消去参数b是解题的关键.
3.D
【分析】令与BC的交点为F,与的交点为M,过点F作FN于点N,根据等边三角形的性质及三角形内心的性质,证明△为等腰三角形,继而证明△△,根据相似三角形对应边成比例的性质,解得,再结合△△及解直角三角形求得,由此可解得DE的长.
【详解】令与BC的交点为F,与的交点为M,过点F作FN于点N,如图,
将△OBC绕点O逆时针旋转30°得到△OB1C1,
点O是边长为2的等边△ABC的内心,
△FOB为等腰三角形,
△△
在△和△中
△△
在△中,
故选:D.
【点睛】本题考查三角形的内切圆与内心、旋转的性质、等边三角形的性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.
4.D
【分析】过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,由勾股定理可求BE=4,根据AAS可证△AEB≌△AGC,得CG=BE=4,易证△BDF∽△BAE,得出=,得出DF=,求最小值,即求DF+CD的最小值,由垂线段最短求解即可.
【详解】解:过点D作DF⊥AB于点F,过点C作CG⊥AB于点G
又于点
∴∠AEB=90°,∠DFB=90°,∠AGC=90°
又∠ABE为公共角
∴△BDF∽△BAE
∴=
又,
∴DF=
∴=DF+CD
∵DF+CD≥CG
∴≥CG
即的最小值为CG的长
在Rt△ABE中
BE===4
∵,∠AEB=90°,∠AGC=90°
又∠A为公共角
∴△AEB≌△AGC(AAS)
∴CG=BE=4
∴的最小值为4
故选:D
【点睛】本题主要考查最短路径中的垂线段最短问题,解决本题借助了全等三角形的判定和性质,等腰三角形的性质,相似三角形以及勾股定理求边长,综合性较强,难度较大.
5.D
【分析】根据作图过程及所作图形可知,得出△BCD是等边三角形;又因为,,推出,继而得出;根据,,可知AD为的角平分线,根据三线合一得出AD垂直平分BC;
四边形ABCD的面积等于的面积与的面积之和,为.
【详解】解:∵
∴△BCD是等边三角形
故选项B正确;
∵,
∴
∴
故选项A正确;
∵,
∴据三线合一得出AD垂直平分BC
故选项C正确;
∵四边形ABCD的面积等于的面积与的面积之和
∴
故选项D错误.
故选:D.
【点睛】本题考查的知识点是等边三角形的判定、全等三角形的判定及性质、线段垂直平分线的判定以及四边形的面积,考查的范围较广,但难度不大.
6.B
【分析】先利用待定系数法求出抛物线解析式,和一次函数解析式,根据抛物线对称轴可判断①,利用抛物线的对称轴与x轴的一个交点可求另一交点可判断②,利用抛物线平移和顶点的位置可判断③,利用二次函数图像与一次函数的图象的位置比较大小,可判断④,根据可得出y1=y2,利用对称性与对称轴关系可判断⑤即可.
【详解】解:∵抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),
∴,
把B点坐标代入得,
解得,
抛物线,
直线()与抛物线交于A,B两点,
∴,
解得,
直线,
①∵对称轴为,则
故①正确;
②∵对称轴为直线,与轴的一个交点是,设另一交点为(m,0),
∴1-m=4-1,
∴m=-2,
与轴的另一个交点是,故②正确;
③∵把抛物线向下平移3个单位,得到,
∴顶点坐标变为,即抛物线与只有一个交点,
∴方程有两个相等的实数根,故③正确;
④当时,二次函数图像在一次函数图像的上方
∴,故④正确;
⑤若,即
即,
则关于函数的对称轴对称,
故,即,故⑤错误,
∴命题正确的有①②③④四个.
故选:B.
【点睛】本题考查了抛物线与的交点,以及函数图象上点的坐标特征,要求学生熟练掌握函数与坐标轴的交点,顶点等点坐标的求法以及这些点代表的意义及函数特征.
7.B
【分析】取的中点,连接、、,根据题意得出和全等,然后得出和全等,设,则,,根据题意列出一元一次方程求出的值得出答案.
【详解】取的中点,连接、、,
,,
,,
为等边三角形,
,
是等边三角形,
,
,
,
,
∵
,
,
,
,
,
,
,
∵为等边三角形,
∴,
∴,
∵是等边三角形,
∴,
设,则,
,
∴
在和中,
,
,
设,则,,
,
,
,
解得,,
即.
故选:B.
【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,平行线的性质,熟练掌握是解题的关键.
8.C
【分析】本题的等量关系为:冰红茶总价钱+矿泉水总价钱=18,冰红茶瓶数+矿泉水瓶数≥7,然后整理求非负整数解即可.
【详解】解:设买冰红茶x瓶、矿泉水y瓶,
根据题意得 ,(且x、y均为非负整数)
则,
所以有3种购买方式,故选C.
【点睛】本题主要考查了二元一次方程的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系,讨论出符合条件的整数解.
9.ACD
【分析】利用待定系数法将各点坐标两两组合代入,求得抛物线解析式为 ,再根据对称轴直线 求解即可得到A选项是正确答案,由抛物线解析式为,令 ,求解即可得到抛物线与x轴的交点坐标(-1,0)和(2,0),从而判断出B选项不正确,令关于x的一元二次方程 的根的判别式当,解得 ,从而得到C选项正确,根据抛物线图象的性质由 ,推出 ,从而推出 ,得到D选项正确.
【详解】当抛物线图象经过点A和点B时,将A(1,-2)和B(2,-2)分别代入,
得,解得 ,不符合题意,
当抛物线图象经过点B和点C时,将B(2,-2)和C(2,0)分别代入,
得,此时无解,
当抛物线图象经过点A和点C时,将A(1,-2)和C(2,0)分别代入得,解得,因此,抛物线经过点A和点C,其解析式为,抛物线的对称轴为直线 ,故A选项正确,
因为,所以 ,抛物线与x轴的交点坐标是(-1,0)和(2,0),故B选项不正确,
由得,方程根的判别式 当 , 时, ,当时,即,解得 ,此时关于x的一元二次方程有两个不相等的实数根,故C选项正确,
因为抛物线与x轴交于点(-1,0)和(2,0),且其图象开口向上,若P(m,n)和Q(m+4,h)都是抛物线上的点,且n<0,得 ,又得 ,
所以h>0,故D选项正确.
故选ACD.
【点睛】本题考查抛物线与x轴的交点 根的判别式 二次函数的性质及二次函数图象上点的坐标特征,解题的关键是利用数形结合思想,充分掌握求二次函数的对称轴及交点坐标的解答方法.
10.BD
【分析】连接,,,,交于,在正六边形中求得,推得,易得,,,设,则,分别求得计算即可.
【详解】解:连接,,,,交于,
∵六边形为正六边形,
∴,,
∴,
∴,,,
∴四边形是矩形,
在中,,∴,
故
∴,,
∵,,
∴
则,,
∴,
设,则,
∴,
,
,
,
,
,
故;
;
;
;
故选:BD.
【点睛】本题考查了正多边形的性质,等腰三角形的性质,勾股定理,三角形面积公式,矩形的判定和性质,角所对的直角边等于斜边的一半等,熟练掌握正多边形的性质是解题的关键.
11.BCD
【分析】延长,交于点,根据平行四边形的性质,矩形的性质,以及平行线分线段成比例,逐一进行判断即可.
【详解】如图,延长,交于点,
在平行四边形中,,
,
,与不一定相等,
不一定成立,
即不一定相等,故A选项不符合题意;
在矩形中,
,,
,
在平行四边形中,
,
,
,
,
,
,,
,
,故B选项正确;
,,
,,
在矩形中,
,
,故C选项正确;
点为中点,,
点为中点,同理可得点为中点,
∴,,
设,则,
,,
,
,
,故D选项正确.
故选BCD.
【点睛】本题考查平行四边形的性质,矩形的性质,平行线分线段成比例,配方法的应用.熟练掌握相关性质,并灵活运用,根据题意正确的画出图形,利用数形结合的思想进行求解,是解题的关键.
12.ABD
【分析】当为CD中点时,设则,由勾股定理列方程求解,进一步求得的值,进而可判断A的正误;当三边之比为3:4:5时,设,,,由可求a 的值,进一步求得的值,进而可判断B的正误;过点A作,垂足为H,连接,AG,先证,可得,,再证,可得,由此证得周长=16,进而可判断C的正误;过点E作EM⊥BC,垂足为M,连接交EM,EF于点N,Q,证明,进而可判断D的正误.
【详解】:∵为CD中点,正方形ABCD的边长为8,
∴,
由折叠的性质,设则,
在中,由勾股定理得,即42+(8﹣x)2=x2,
解得x=5,
∴AE=5,DE=3,
∴,
故A正确;
当三边之比为3:4:5时,设,,,则,
∵,
∴,
解得:,
∴,,
故B正确;
过点A作,垂足为H,连接,AG,则,
由折叠的性质可知,
∴,
∵,
∴,
∵,
∴,
∴,
在和中
,
∴,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∴周长
,
∴当在CD上移动时,周长不变,
故C错误;
如图,过点E作EM⊥BC,垂足为M,连接交EM,EF于点N,Q,
∴,,
∴,
由翻折可知:EF垂直平分,
∴,
∴,
∴,
在和中,
,
,
∴,
故D正确.
故选:ABD.
【点睛】本题考查了正方形的性质,折叠的性质,勾股定理,全等三角形的判定与性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.
13. 90
【分析】(1)设,画出图形,由得,由得,由得,再利用三角形内角和定理得到答案;
(2)求出是定值,点P在以M为圆心,长为半径的圆上,连接,交圆M于点,得到,过点M作,根据三角函数求出,,由勾股定理求出连接,则,当P与重合时,有最小值,求出即可.
【详解】解:(1)设,如图,
则,
由题意可得,M是和中垂线上的点,
∴即,
∵,
∴,
∵,
∴,
又,
∴,
∵,
∴,
∴,
又,,
在中,有,
∴,
即,
即;
故答案为:90
(2)如图,
∵,
∴,即,
在中,,
∵是定值,
∴是定值,
即点P在以M为圆心,长为半径的圆上,
连接,交圆M于点,
由(1)中结论可知,又,
∴,
又,
∴,
过点M作,
∵,
∴,
∵,
∴,即,
∴,即,
又,
∴,
连接,则,
当P与重合时,有最小值,
∵,即,即
∴,即最小值为
综上,最小值为,
故答案为:.
【点睛】此题考查了线段垂直平分线的性质,三角形内角和定理,锐角三角函数,动点问题,勾股定理,正确作出辅助线及掌握各知识点是解题的关键.
14.①②③④⑤
【分析】根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG//CF;分别求出S△EGC与S△AFE的面积比较即可;求得∠GAF=45°,∠AGB+∠AED=180°-∠GAF=135°,即可得到答案.
【详解】解:∵AB=AD=AF,AG=AG,∠B=∠AFG = 90°,
∴,
故①正确;
∵,
∴,
∴,
设,则,
在中,由勾股定理得:,
即:,
解得:,
∴,
∴,
故②正确;
∵,
∴,
∵是等腰三角形,,
∵Rt△ABG≌Rt△AFG,
∴,
∴,
∴,
∴,
故③正确;
∵,,
∴,
故④正确;
∵,
又∵,
∴,
∴,
故⑤正确;
故答案为:①②③④⑤.
【点睛】本题考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想与方程思想的应用.
15.
【分析】连接交于点,连接易证得,得到点G为的中点,所以是中位线,可得到,求最小值即为求最小值的一半,随着点E的变化,点M在上动,即当时,有最小值,然后在中,借助三角函数计算即可.
【详解】解:如图,连接交于点,连接,过点作于点N,
∵点为中点,
∴,
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴点G为的中点,
∵点H为的中点,
∴是中位线,
∴,
∴求最小值即为求最小值的一半,随着点E的变化,点M在上动,即当时,有最小值,即最小值=,
∵是的中点,
∴,
∵
∴,
∴.
故答案为:
【点睛】本题主要考查动点最值,根据条件做出辅助线,利用中位线转化所求线段,然后借助点到线距离垂线段最短计算即可.
16.
【分析】取点D的特殊位置:当点D与点F重合时,当点D在CA延长线与圆A的交点时,当CD与圆A相切时,确定FE的长度都是0.5,从而得到点E的运动轨迹是以点F为圆心,0.5为半径的圆上运动,故而得到线段BE的最大值与最小值,由此得到答案.
【详解】∵△ABC为等边三角形,AB=2,
∴AC=AB=2,
设AC交圆A于点F,
∵点D是以A为圆心,半径为1的圆上一动点,
∴当点D与点F重合时,如图1,FE=0.5,
当点D在CA延长线与圆A的交点时,如图2,FE=0.5,
当CD与圆A相切时,FE=0.5,
故点E在以点F为圆心,0.5为半径的圆上运动,
当点B、F、E三点共线时,线段BE有最大值和最小值,如图4:
∵AF=1,AC=2,
∴FC=1,
∴点F是AC的中点,
∵△ABC是等边三角形,
∴BF⊥AC,
∴BF= ,
线段BE的最大值=,最小值=,
∴线段BE的最大值与最小值之和为,
故答案为:.
【点睛】此题考查圆与动点问题,圆的性质,圆的切线的性质定理,等边三角形的性质,勾股定理,根据题意理解点D运动的路线得到点E的运动轨迹是解题的关键.
17.(1)证明见解析;(2) 四边形的面积为.
【详解】【分析】(1)根据尺规作图可知AF平分∠BAC,再根据DF//AC,可得AD=DF,再由两组对边分别平行的四边形是平行四边形可得四边形AEFD是平行四边形,继而可得平行四边形AEFD是菱形,根据“亲密菱形”的定义即可得证;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,可证得△BDF∽△BAC,根据相似三角形的性质可求得a=4,过D作DG⊥AC,垂足为G,在Rt△ADG中, DG=2,继而可求得面积.
【详解】(1)由尺规作图可知AF平分∠BAC,
∴∠DAF=∠EAF,
∵DF//AC,∴∠DFA=∠EAF,∴∠DAF=∠DFA,∴AD=DF,
∵FD//AC,FE//AB,∴四边形AEFD是平行四边形,
∴平行四边形AEFD是菱形,
∵∠BAC与∠DAE重合,点F点BC上,
∴菱形AEFD为△ABC的“亲密菱形”;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,
∵DF//AC,∴△BDF∽△BAC,
∴BD:BA=BF:AC,
即(6-a):6=a:12,
∴a=4,
过D作DG⊥AC,垂足为G,
在Rt△ADG中,∠DAG=45°,∴DG=AD=2,
∴S菱形AEFD=AE DG=8,
即四边形AEFD的面积为8.
【点睛】本题考查了尺规作图,新概念题,菱形的判定与性质等,正确理解新概念是解题的关键.
18.(1)∠ABP=30°;(2)3;(3)
【分析】(1)证明,推出即可解决问题.
(2)由翻折可知:EF垂直平分PB,设,求出即可解决问题.
(3)如图3﹣1中,作点P关于CD的对称点N,连接FN交CD于G,此时 ,以PF为直径作圆交CD 于,此时 ,.①当点G与G2重合时,满足条件,易证 ,设.构建方程求出a与b的关系即可解决问题.②当G1,与G2重合时,满足条件,此时以PF为直径的圆与CD相切,设,构建方程求出m与n的关系即可解决问题.
【详解】解:(1)∵ ,
∴,
由翻折可知:,
∴ ,
∵四边形ABCD是矩形,
∴,
∴,
∴,
∵ ,
∴ ,
∴.
(2)由翻折可知:EF垂直平分PB,设,
在中,∵ ,
∴,
在中, ,
∴ ,
∴ ,
∴ ,
∴ .
(3)如图3﹣1中,作点P关于CD的对称点N,连接FN交CD于G,此时,以PF为直径作圆交CD 于G1,G2,此时 ,.
①当点G与G2重合时,满足条件,易证,设 ,
则: ,
∵ ,
∴ ,
∴ ,
∴ .
②当G1,与G2重合时,满足条件,此时以PF为直径的圆与CD相切,设 ,
则:, ,
∵,
∴ ,
∴,
∴,,
∴ .
【点睛】本题属于相似三角形综合题,考查了相似三角形的判定和性质,解题的关键是学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
19.(1);(2)能,理由见解析.
【详解】试题分析:(1)直接利用待定系数法求二次函数解析式进而得出答案;
(2)首先利用待定系数法求出一次函数解析式,进而令y=45,有45=-x+95,求出x的值,进而得出讲课后注意力不低于45的时间.
(1)当0≤t≤10时,设抛物线的函数关系式为y=ax2+bx+c.由于它的图象经过点(0,25),(4,45),(10,60),
所以,
解得:,
所以;
(2)当20≤x≤40时,设函数解析式为:y=kx+d,将(20,60),(40,25)代入得:
,
解得:
∴,
令y=45,有45=-x+95,
解得:x=,
即讲课后第分钟时注意力不低于45,
当0≤x≤10时,令y=45,有45=-x2+6x+25,
解得:x1=4,x2=20(舍去),
即讲课后第4分钟时,注意力不低于45,
所以讲课后注意力不低于45的时间有(分钟)>24(分钟),
所以老师可以经过适当的安排,使学生在探究这道数学题时,注意力指数不低于45.
考点:二次函数的应用.
20.(1)①等腰;②1
(2)是等腰直角三角形,证明见解析
(3)的取值范围是
【分析】(1)①根据折叠的性质得出垂直平分,根据垂直平分线的性质即可得出是等腰三角形;
②由折叠得,若是等边三角形,则,根据矩形的性质得出,
(2)由得,根据勾股定理的逆定理得出,证明是直角三角形,进而即可得出结论;
(3)连接,以点为圆心,长为半径作圆交于点,交于点,得出,即点在上运动,连接、、,则,当点落在矩形内部包括边时,则.
【详解】(1)如图1,①将矩形纸片沿折叠,点与点重合,
垂直平分,
,
是等腰三角形,
故答案为:等腰.
②由折叠得,
若是等边三角形,则,
四边形是矩形,
,
故答案为:.
(2)是等腰直角三角形,
证明:如图,由得,
∴,
∵,
∴
∴,
是直角三角形,
,
是等腰直角三角形.
(3)如图,连接,以点为圆心,长为半径作圆交于点,交于点,
,,,
,
,
点在上运动,
连接、、,则,
,
四边形是矩形,
,,
,
,
当点落在矩形内部包括边时,则,
即,
∴的取值范围是.
【点睛】本题考查了矩形与折叠问题,等腰三角形的性质与判定,等边三角形的性质与判定,勾股定理,圆外一点到圆的最值问题,轴对称的性质,综合运用以上知识是解题的关键.
21.(1)
(2)保持不变,见解析
(3)线段AD的最大值为,最小值为
【分析】(1)在Rt△DEF中,根据,,求出,在Rt△ABC中,根据,,求出,在Rt△GEB中,根据,,求出,算出AG,证明,得出即可;
(2)过B点作,交射线EM于点G,连接AG,根据,,证明,得出,,证明,得,进而得出即可;
(3)由题意得,点A在以C为圆心,以CA为半径的圆上移动,当点D、A、C三点共线时,是最小值,是最大值,然后求出DC、AC即可得出答案.
(1)
解:∵在Rt△DEF中,,,
∴,
∵在Rt△ABC中,,,
∴,
,
∴,
∵在Rt△GEB中,
∴
∴,
,
∴,
∴.
故答案为:.
(2)
保持不变.理由如下:
过B点作,交射线EM于点G,连接AG,
∵,
∴,,
∵在中,,
∴,,
∴,,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴;
(3)
由题意得,点A在以C为圆心,以CA为半径的圆上移动,如图所示:
∴当点D、A、C三点共线时,是最小值,是最大值,
∵在中,,,
∴,
∵在Rt△ABC中,,,
∴,
∴线段AD的最大值为,最小值为.
【点睛】本题主要考查了解直角三角形,特殊角的三角函数值,勾股定理,三角形相似的判定和性质,平行线的判定和性质,根据题意得出点A在以C为圆心,以CA为半径的圆上移动,当点D、A、C三点共线时,是最小值,是最大值,是解决问题的关键.
22.(1)
(2)见解析
【分析】(1)由垂直平分线的性质可得,由勾股定理可求,的长,即可求解;
(2)在上截取,在上截取,连接.由“”可得,可得,,可证,通过证明,可得,结合题意即可得出,进而得出,最后由三角形中位线的性质即可得出结论.
【详解】(1)解:如图,连接,
,,
.
垂直平分,
∴,,
∴,
∴,
∴;
(2)证明:如图,在上截取,在上截取,连接.
在和中,,
∴,
∴,,,
∴.
又∵,
∴,
,
.
,,
,
,
,
,
,
.
【点睛】本题考查矩形的性质,勾股定理,线段垂直平分线的性质,相似三角形的判定和性质,全等三角形的判定和性质等知识,添加恰当辅助线构造全等三角形是解题的关键.
同课章节目录
