21.2.4 一元二次方程的根与系数的关系课件(32张PPT)
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 15:17:26 | ||
图片预览











文档简介
(共32张PPT)
21.2.4 一元二次方程的根与系数的关系
人教版九年级上册
知识回顾
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
3.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a≠0).
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
2.一元二次方程的求根公式:
教学目标
1.探索一元二次方程的根与系数的关系.
2.不解方程利用一元二次方程的根与系数的关系解决问题.
新知导入
问题1:
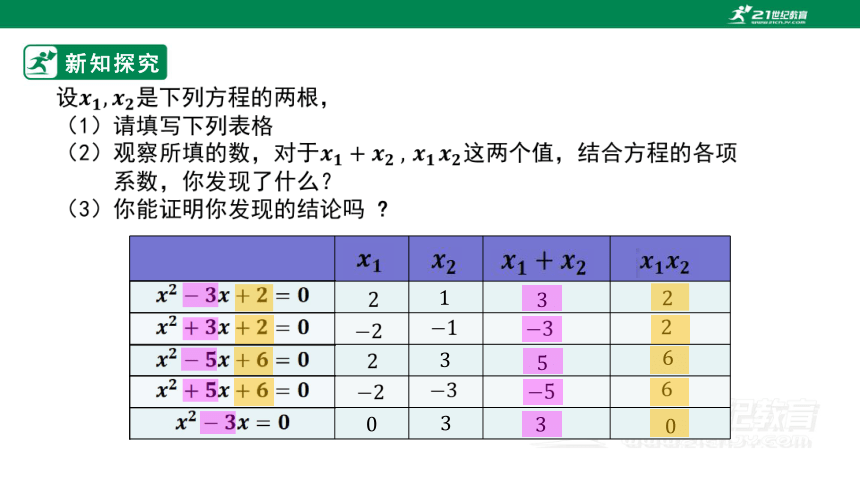
新知探究
问题1:
解:设长和宽分别是方程的两个根
和
长方形的周长:
长方形的面积:
新知探究
0
1
3
3
3
3
5
0
6
新知探究
分析:
因式分解法
新知探究
解:
新知探究
化二次项系数为1
方法一:
类比x2+px+q=0
新知探究
问题3:
方法二:
新知探究
平方差公式
新知探究
b
c
两根之和
两根之积
前提条件
新知探究
问题1:
由根与系数关系得
方法二:
长方形的周长:
2(x1+x2)
=2×3
=6
长方形的面积:
x1×x2=1
新知练习
练习:
解:
解:
解:
新知典例
例2:
方法一:
新知典例
代入
方法二:
,
则:
典例回顾
例2:
方法一:
方法二:
,
新知探究
例3:
你能写出多少个?
新知探究
例3:
由一元二次方程根与系数的关系
令a=1,可得符合题意的方程
新知探究
利用根与系数的关系求值
根据完全平方公式
解题策略:
先变形
例4:
=(x1+x2)2-2x1x2
新知探究
解题策略:
先变形
例4:
新知小节
与一元二次方程 ax2+bx+c=0(a≠0) 的两个根 x1,x2 有关的几个代数式的变形:
新知练习
已知关于 x 的一元二次方程 2x2-mx-2m+1=0 的两根的平方和是 ,求 m 的值.
解:设方程的两根分别为 x1,x2,由已知得
因为 ,所以,
所以,解得 m1=-11,m2=3.
当 m= -11时,方程为 2x2+11x+23=0,121-4×2×23=-63<0,
方程无实数根,不合题意,应舍去;
当 m=3时,方程为 2x2-3x-5=0,Δ=(-3)2-4×2×(-5)=49>0,
方程有两个不相等的实数根.综上所述,m 的值为 3.
求解此类问题时,必须将求出的字母值代回原方程进行检验,看是否满足判别式Δ>0 ,否则可能会多解.
课堂总结
一元二次方程 ax2+bx+c=0(a≠0) 的根与系数的关系 数学语言 若 ax2+bx+c=0(a≠0) 的两个根为 x1,x2,则 x1+x2= ,x1x2= .
文字语言 一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件 1.方程是一元二次方程,即二次项系数不为 0;
2.方程有实数根,即 Δ≥0.
重要结论 1.若一元二次方程 x2+px+q=0 的两根为 x1,x2,则 x1+x2=-p,x1x2=q.
2.以实数 x1,x2 为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
课堂总结
利用根与系数的关系求值
解题策略:
先变形
课堂练习
1.已知实数 a,b 分别满足 a2-6a+4=0,b2-6b+4=0,且 a≠b,则 的值是( )
A. B. C. D.
解:因为 a2-6a+4=0 和 b2-6b+4=0 两个等式的形式相同,且 a≠b,
所以 a,b 可以看成是方程 x2-6x+4=0 的两个根,
所以 a+b=6,ab=4,
从而 ,故选A.
A
课堂练习
2.已知 是方程 x2-3x-4=0 的两个实数根,则 的值为 .
0
解:根据题意得 α+β=3,αβ=-4,
所以原式 = α(α+β)-3α
=3α-3α
=0.
课堂练习
3.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
解:(1)方程化为 x2-3x-15=0,
x1+x2=-(-3)=3,x1x2=-15.
(2)方程化为 3x2+4x+1=0,
x1+x2=- , x1x2= .
(3)方程化为 x2-x-1=0,
x1+x2=-(-1)=1,x1x2=-1.
(4)方程化为 2x2-4x+1=0,
x1+x2=-=2, x1x2 =.
课堂练习
4.已知关于 x 的一元二次方程 x2-6x+q=0 有一个根为 2,求方程的另一根和 q 的值.
解:设方程的另一个根为 a,则 2+a=-(-6)=6,
解得 a=4,
则 q=2×4=8.
课堂练习
解:根据题意,得 x1+x2=-3,x1x2=-1,
所以 x1-1+x2-1=-5, (x1-1)(x2-1)=x1x2- (x1+x2)+1=-1+3+1=3,
所以以 x1-1 和 x2-1 为根的一个一元二次方程可以是 x2+5x+3=0(答案不唯一).
5.已知 x1,x2 是方程 x2+3x-1=0 的两个根,求以x1-1和x2-1为根的一元二次方程.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.2.4 一元二次方程的根与系数的关系
人教版九年级上册
知识回顾
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
3.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a≠0).
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
2.一元二次方程的求根公式:
教学目标
1.探索一元二次方程的根与系数的关系.
2.不解方程利用一元二次方程的根与系数的关系解决问题.
新知导入
问题1:
新知探究
问题1:
解:设长和宽分别是方程的两个根
和
长方形的周长:
长方形的面积:
新知探究
0
1
3
3
3
3
5
0
6
新知探究
分析:
因式分解法
新知探究
解:
新知探究
化二次项系数为1
方法一:
类比x2+px+q=0
新知探究
问题3:
方法二:
新知探究
平方差公式
新知探究
b
c
两根之和
两根之积
前提条件
新知探究
问题1:
由根与系数关系得
方法二:
长方形的周长:
2(x1+x2)
=2×3
=6
长方形的面积:
x1×x2=1
新知练习
练习:
解:
解:
解:
新知典例
例2:
方法一:
新知典例
代入
方法二:
,
则:
典例回顾
例2:
方法一:
方法二:
,
新知探究
例3:
你能写出多少个?
新知探究
例3:
由一元二次方程根与系数的关系
令a=1,可得符合题意的方程
新知探究
利用根与系数的关系求值
根据完全平方公式
解题策略:
先变形
例4:
=(x1+x2)2-2x1x2
新知探究
解题策略:
先变形
例4:
新知小节
与一元二次方程 ax2+bx+c=0(a≠0) 的两个根 x1,x2 有关的几个代数式的变形:
新知练习
已知关于 x 的一元二次方程 2x2-mx-2m+1=0 的两根的平方和是 ,求 m 的值.
解:设方程的两根分别为 x1,x2,由已知得
因为 ,所以,
所以,解得 m1=-11,m2=3.
当 m= -11时,方程为 2x2+11x+23=0,121-4×2×23=-63<0,
方程无实数根,不合题意,应舍去;
当 m=3时,方程为 2x2-3x-5=0,Δ=(-3)2-4×2×(-5)=49>0,
方程有两个不相等的实数根.综上所述,m 的值为 3.
求解此类问题时,必须将求出的字母值代回原方程进行检验,看是否满足判别式Δ>0 ,否则可能会多解.
课堂总结
一元二次方程 ax2+bx+c=0(a≠0) 的根与系数的关系 数学语言 若 ax2+bx+c=0(a≠0) 的两个根为 x1,x2,则 x1+x2= ,x1x2= .
文字语言 一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件 1.方程是一元二次方程,即二次项系数不为 0;
2.方程有实数根,即 Δ≥0.
重要结论 1.若一元二次方程 x2+px+q=0 的两根为 x1,x2,则 x1+x2=-p,x1x2=q.
2.以实数 x1,x2 为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
课堂总结
利用根与系数的关系求值
解题策略:
先变形
课堂练习
1.已知实数 a,b 分别满足 a2-6a+4=0,b2-6b+4=0,且 a≠b,则 的值是( )
A. B. C. D.
解:因为 a2-6a+4=0 和 b2-6b+4=0 两个等式的形式相同,且 a≠b,
所以 a,b 可以看成是方程 x2-6x+4=0 的两个根,
所以 a+b=6,ab=4,
从而 ,故选A.
A
课堂练习
2.已知 是方程 x2-3x-4=0 的两个实数根,则 的值为 .
0
解:根据题意得 α+β=3,αβ=-4,
所以原式 = α(α+β)-3α
=3α-3α
=0.
课堂练习
3.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
解:(1)方程化为 x2-3x-15=0,
x1+x2=-(-3)=3,x1x2=-15.
(2)方程化为 3x2+4x+1=0,
x1+x2=- , x1x2= .
(3)方程化为 x2-x-1=0,
x1+x2=-(-1)=1,x1x2=-1.
(4)方程化为 2x2-4x+1=0,
x1+x2=-=2, x1x2 =.
课堂练习
4.已知关于 x 的一元二次方程 x2-6x+q=0 有一个根为 2,求方程的另一根和 q 的值.
解:设方程的另一个根为 a,则 2+a=-(-6)=6,
解得 a=4,
则 q=2×4=8.
课堂练习
解:根据题意,得 x1+x2=-3,x1x2=-1,
所以 x1-1+x2-1=-5, (x1-1)(x2-1)=x1x2- (x1+x2)+1=-1+3+1=3,
所以以 x1-1 和 x2-1 为根的一个一元二次方程可以是 x2+5x+3=0(答案不唯一).
5.已知 x1,x2 是方程 x2+3x-1=0 的两个根,求以x1-1和x2-1为根的一元二次方程.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
