图形的相似1[下学期]

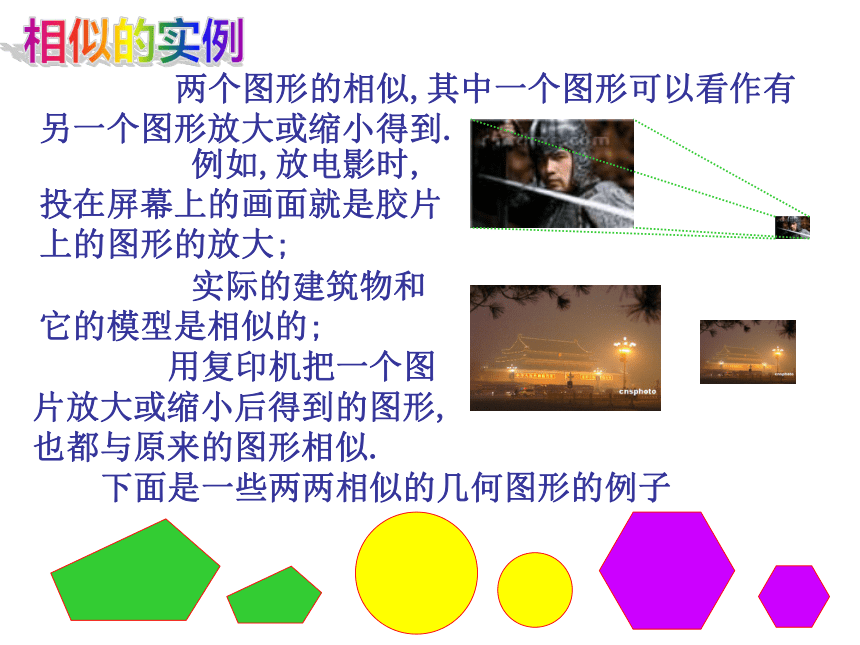
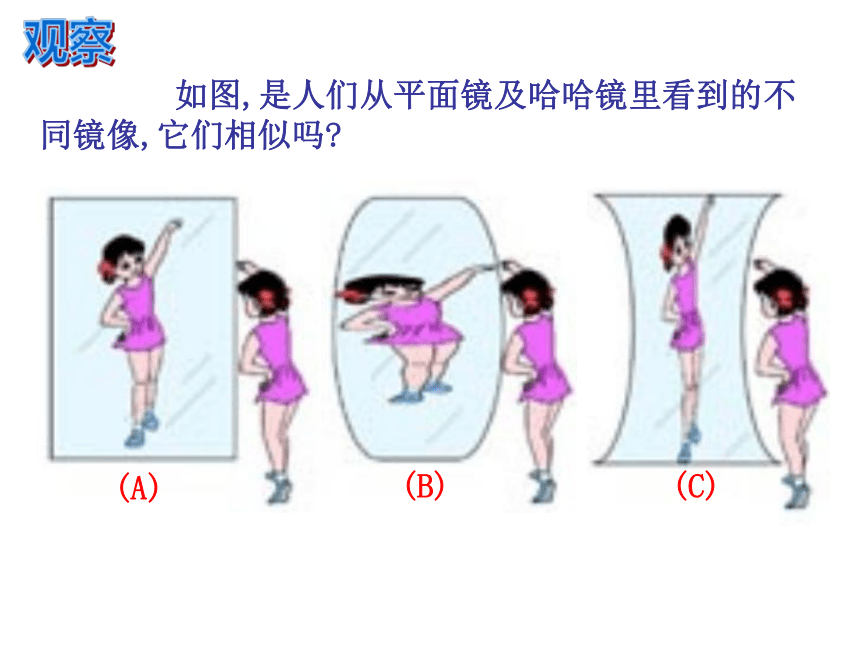
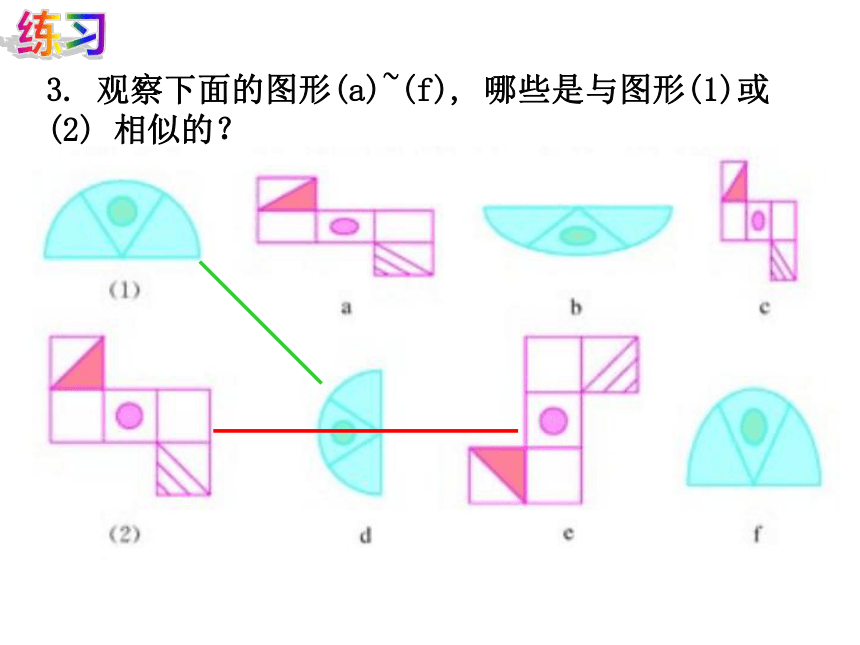
课件15张PPT。第27章 孝感市文昌中学27.1 图形的相似(1)相似 在现实生活中,我们经常见到形状相同的图形. 如国旗上大小不同的五角星,还有不同尺寸同底版的相片等等. 这些形状相同的图形之间,在数量关系和位置关系上有什么规律吗?地图上的比例尺是怎样得到的?怎么才能按要求放大或缩小一张美丽的图片?相似图形相似图形相似图形相似图形图形的相似 形状相同大小不一定相同的图形. 想一想:我们刚才所见到的图形有什么相同和不同的地方?相同点: 形状相同;不同点: 大小不一定相同.相似图形:相似的实例 两个图形的相似,其中一个图形可以看作有另一个图形放大或缩小得到. 例如,放电影时,投在屏幕上的画面就是胶片上的图形的放大; 实际的建筑物和它的模型是相似的; 用复印机把一个图片放大或缩小后得到的图形,也都与原来的图形相似.下面是一些两两相似的几何图形的例子观察 如图,是人们从平面镜及哈哈镜里看到的不同镜像,它们相似吗?(A)(B)(C)练习1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?2.观察下面的图形中哪些是相似的？1233. 观察下面的图形(a)~(f), 哪些是与图形(1)或(2) 相似的？练习练习4. 观察下面的图形(1)~(13), 找出相似的图形.思考 图(1)中的正△A1B1C1是由正△A B C放大后得到的,观察这两个图形它们的对应角有什么关系?
对应边呢? ABCA1B1C1(1) 对于图(2)中两个相似的正六边形,你是否也能得到类似的结论？ (2)对比图(1)中的正△A1B1C1和正△A B C,可得:∠A=∠A’,∠B=∠B’,∠C=∠C’ 这说明,正三角形都是相似的,它们的对应角相等,对应边的比相等.思考 图(1)中的正△A1B1C1是由正△A B C放大后得到的,观察这两个图形它们的对应角有什么关系?
对应边呢? ABCA1B1C1(1)结论: 1.相似的正多边形对应角相等,对应边的比相等. 2.所有边数相同的正多边形一定多是相似多边形. 对于图(2)中两个相似的正六边形,你是否也能得到类似的结论？ (2)8561060°50° 如图:△ABC和△A’B’C’是相似三角形,根据已知条件,填空: A’B’=____ , B’C’=____ , 161250°70°练习∠B=____ , ∠C=______.比例线段 对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,那么就说这四条线段是成比例线段,简称比例线段. 例如四条线段a、b、c、d满足(即 ad=bc)则称 a、b、c、d是成比例线段.注意:(1)四条线段 a、b、c、d成比例,记作:或 a∶b=c∶d, 而不能写成 也就是说,四条线段成比例时,要将这四条线段按顺序列出. (2) 比例式a、b、c、d称为或 a∶b=c∶d中, 其中a、d称为比例外项,b、c称为比例内项,d叫第四比例项.比例项,(3) 如果 , 那么线段b叫线段a、c的比例中项. 小结形状相同大小不一定相同的图形.1. 相似图形:2.结论:(2)所有边数相同的正多边形一定多是相似多边形.(1)相似的正多边形对应角相等,对应边的比相等. 对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,那么就说这四条线段是成比例线段,简称比例线段. 3. 比例线段:a、b、c、d 称为比例项,或 a∶b=c∶d, 其中a、d 称为比例外项,b、c 称为比例内项,d叫第四比例项.若线段 a、b、c、d成比例,记作:作业:P40
习题27.1/1、2、3再见