1.1 第1课时 集合的概念-2022-2023学年高一数学新教材配套课件(人教A版必修第一册)(共33张PPT)
文档属性
| 名称 | 1.1 第1课时 集合的概念-2022-2023学年高一数学新教材配套课件(人教A版必修第一册)(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 942.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 09:01:57 | ||
图片预览











文档简介
(共33张PPT)
第1课时 集合的概念
第一章 1.1 集合的概念
学习目标
1.通过实例了解集合的含义以及集合中元素的特性.(重难点)
2.掌握元素与集合之间的关系并能用符号表示.(重点)
3.掌握常用数集的表示符号并会应用.(重点)
1
自主学习
自主探究一
初中我们接触了那些集合?
数集:自然数的集合,有理数的集合...
点集:圆(同一平面内到一个定点的距离等于定长的点的集合)
线段的垂直平分线(到一条线段的两个端点的距离相等的点的集合)
自主探究一
看下面的例子:
(1)1~10之间的所有偶数;
(2)某中学今年入学的全体高一学生;
(3)所有的正方形;
(4)到直线 l 的距离等于定长 d 的所有点;
(5)方程 的所有实数根;
(6)地球上的四大洋。
上述每个问题都由若干个对象组成,每组对象的全体分别形成一个集合,集合中的每个对象都称为元素.
组成集合的元素所属对象是否有限制?集合中元素个数的多少是否有限制?
知识点一 元素与集合的概念
1.元素:一般地,把 统称为元素(element),常用小写的拉丁字母_____ ___表示.
2.集合:把一些 组成的总体叫做集合(set),(简称为 ),常用大写拉丁字母 表示.
研究对象
a,b,c…
元素
集
A, B,C…
自主探究一
任意一组对象是否都能组成一个集合?集合中的元素有什么特征?
思考1:咱们班身材较高的人能否构成一个集合?由此说明什么?
集合中的元素必须是确定的.(确定性)
思考2:在一个给定的集合中能否有相同的元素?由此说明什么?
集合中的元素是不重复出现的.(互异性)
思考3:咱们班的全体同学组成一个集合,调整座位后这个集合有没有
变化?由此说明什么?
集合中的元素是没有顺序的.(无序性)
自主探究二
思考4:两个集合的元素是一样的,那么这两个集合是相等的吗?
只要构成两个集合的元素一样,我们就称这两个集合是相等的.
知识点二 集合中元素的特性
1.集合中元素的特性:给定的集合,它的元素必须满足 、 、 .
2.集合相等:指构成两个集合的元素是 的.
无序性
确定性
互异性
一样
自主探究二
小试牛刀
1.组成集合的元素一定是数.( )
2.接近于0的数可以组成集合.( )
3.分别由元素0,1和1,0组成的两个集合是相等的.( )
4.一个集合中可以找到两个相同的元素.( )
×
×
×
√
自主探究三
思考:设集合A表示“1~20以内的所有质数”,那么3,4,5,6这四个元素
哪些在集合A中?哪些不在集合A中?
知识点三 元素与集合的关系
1.属于:如果a是集合A的元素,就说a 集合A,记作 .
2.不属于:如果a不是集合A中的元素,就说a 集合A,记作 .
属于
a∈A
不属于
a A
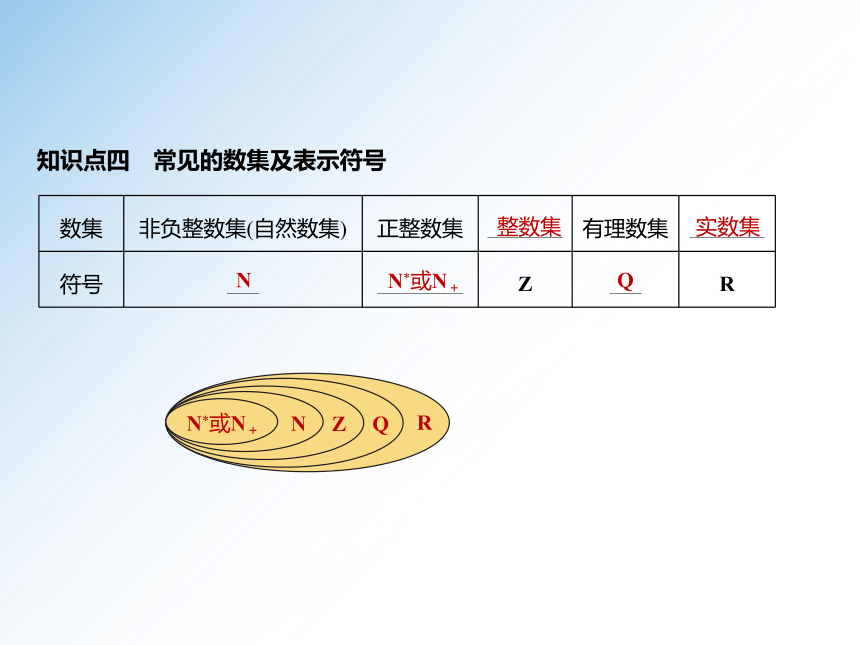
数集 非负整数集(自然数集) 正整数集 _______ 有理数集 _______
符号 ___ ________ Z ___ R
知识点四 常见的数集及表示符号
整数集
实数集
N
N*或N+
Q
N*或N+
N
Z
Q
R
小试牛刀
5.用符号“ ”或“ ”填空:
(1) 3.14_______ Q
(2) π_______ Q
(3) 0_______
(4) ____Z
N+
2
经典例题
题型一 对集合的理解
例1 (1)1.下列说法中,正确的有____.(填序号)
①中国各地的美丽乡村;
②单词book的所有字母组成的集合的元素共有4个;
③集合M中有3个元素a,b,c,其中a,b,c是△ABC的三边长,则△ABC不可能是等腰三角形;
④将小于10的自然数按从小到大的顺序排列和按从大到小的顺序排列分别得到不同的两个集合.
解析 ①中“美丽”标准不明确,不符合确定性,②不正确. book的字母o有重复,共有3个不同字母,元素个数是3.③正确. 集合M中有3个元素a,b,c,所以a,b,c都不相等,它们构成的三角形三边不相等,故不可能是等腰三角形.④不正确. 小于10的自然数不管按哪种顺序排列,里面的元素都是0,1,2,3,4,5,6,7,8,9这10个数,集合是相同的,和元素的排列顺序无关.
③
总结: 判断一组对象是否为集合的三依据
(1)确定性:负责判断这组元素是否构成集合.
(2)互异性:负责判断构成集合的元素的个数.
(3)无序性:表示只要一个集合的元素确定,则这个集合也随之确定,与元素之间的排列顺序无关.
跟踪训练
1.对于以下说法,正确的有______.(填序号)
①绝对值非常小的全体实数构成一个集合;
②长方体的全体构成一个集合;
③全体无实数根的一元二次方程构成一个集合;
④ 组成的集合含有四个元素。
解析 ①中“绝对值非常小”标准不明确,不符合确定性,②正确.③正确. ④不正确,不满足互异性
②③
题型二 元素与集合的关系
例2 下列关系中正确的个数为
A.1 B.2 C.3 D.4
√
②-1 N,②正确;
③∵π是实数,∴π∈R,故③错误;
④∵|-4|=4是整数,∴|-4|∈Z,故④正确.
总结:判断元素和集合关系的两种方法
(1)直接法:集合中的元素是直接给出的.
(2)推理法:对于某些不便直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可.
跟踪训练
2.给出下列说法:
①R中最小的元素是0;
②若a∈Z,则-a Z;
③若a∈Q,b∈N*,则a+b∈Q.
其中正确的个数为
A.0 B.1 C.2 D.3
解析 实数集中没有最小的元素,故①不正确;
对于②,若a∈Z,则-a也是整数,故-a∈Z,所以②也不正确;
只有③正确.
√
题型三 元素特性的应用
例3 (1)设集合A由元素 构成,求实数 k 的取值范围。
解 由集合中元素的互异性知
故实数k的取值范围是
题型三 元素特性的应用
例3 (2)已知集合A含有两个元素a-3和2a-1,若-3∈A,试求实数a的值.
解 ∵-3∈A, ∴-3=a-3或-3=2a-1,
①若-3=a-3,
则a=0,
此时集合A中含有两个元素-3,-1,符合题意;
②若-3=2a-1,则a=-1,
此时集合A中含有两个元素-4,-3,符合题意;
综上所述,a=0或a=-1.
总结:由集合中元素的特性求解字母取值(范围)的步骤
跟踪训练
3.(1)如果有一集合含有两个元素: ,则实数x的取值范围是________.
解 由集合中元素的互异性知 ,解得
故实数x的取值范围是
3.(2)已知集合A由元素0,m, 构成,且 2 A,求实数m的值。
解 ∵2∈A,∴m=2或 =2,
①若m=2,则 =0,不符合题意;
②若 =2,则m=0或m=3,
当m=0时,不符合题意;
当m=3时,此时集合A中含有三个元素0,3,2,符合题意;
综上所述,m=3.
跟踪训练
3
当堂达标
1.下列给出的对象中,能组成集合的是
A.一切很大的数
B.好心人
C.漂亮的小女孩
D.方程x2-1=0的实数根
√
2.下列结论不正确的是
解析 0是有理数,故0∈Q,所以C错误.
√
3.若以集合A的四个元素a,b,c,d为边长构成一个四边形,则这个四边形可能是
A.梯形 B.平行四边形
C.菱形 D.矩形
解析 由于a,b,c,d四个元素互不相同,故它们组成的四边形的四条边都不相等.
√
4.由 组成一个集合A,A中含有3个元素,则实数a的值可以是( )
A.1 B.-2 C.6 D.2
解析 由集合元素的互异性可得 ,解得a≠1,±2.
√
5.已知集合A由元素 构成,且 ,求实数a的值.
解析 ∵-3∈A,∴
①若 则a=0,此时集合A中含有三个元素-3,-1,-4,符合题意;
②若 则a=-1,此时集合A中含有元素为-4,-3,-3,不符合题意;
③若 则a =±1,由②知a=-1不符合题意,
当a=1时,此时集合A中含有三个元素-2,1,-3,符合题意;
综上所述,a=0或a=1.
6.设A是实数集,满足
(1)若 ,则集合A中至少还有几个元素?求出这几个元素。
(2)集合A中能否只含有一个元素?请说明理由。
(3)若 ,证明:
课堂小结
1.知识清单:
(1)元素与集合的概念、元素与集合的关系.
(2)常用数集的表示.
(3)集合中元素的特性及应用.
2.方法归纳:分类讨论.
3.常见误区:忽视集合中元素的互异性.
课堂作业
作业:完成对应练习
第1课时 集合的概念
第一章 1.1 集合的概念
学习目标
1.通过实例了解集合的含义以及集合中元素的特性.(重难点)
2.掌握元素与集合之间的关系并能用符号表示.(重点)
3.掌握常用数集的表示符号并会应用.(重点)
1
自主学习
自主探究一
初中我们接触了那些集合?
数集:自然数的集合,有理数的集合...
点集:圆(同一平面内到一个定点的距离等于定长的点的集合)
线段的垂直平分线(到一条线段的两个端点的距离相等的点的集合)
自主探究一
看下面的例子:
(1)1~10之间的所有偶数;
(2)某中学今年入学的全体高一学生;
(3)所有的正方形;
(4)到直线 l 的距离等于定长 d 的所有点;
(5)方程 的所有实数根;
(6)地球上的四大洋。
上述每个问题都由若干个对象组成,每组对象的全体分别形成一个集合,集合中的每个对象都称为元素.
组成集合的元素所属对象是否有限制?集合中元素个数的多少是否有限制?
知识点一 元素与集合的概念
1.元素:一般地,把 统称为元素(element),常用小写的拉丁字母_____ ___表示.
2.集合:把一些 组成的总体叫做集合(set),(简称为 ),常用大写拉丁字母 表示.
研究对象
a,b,c…
元素
集
A, B,C…
自主探究一
任意一组对象是否都能组成一个集合?集合中的元素有什么特征?
思考1:咱们班身材较高的人能否构成一个集合?由此说明什么?
集合中的元素必须是确定的.(确定性)
思考2:在一个给定的集合中能否有相同的元素?由此说明什么?
集合中的元素是不重复出现的.(互异性)
思考3:咱们班的全体同学组成一个集合,调整座位后这个集合有没有
变化?由此说明什么?
集合中的元素是没有顺序的.(无序性)
自主探究二
思考4:两个集合的元素是一样的,那么这两个集合是相等的吗?
只要构成两个集合的元素一样,我们就称这两个集合是相等的.
知识点二 集合中元素的特性
1.集合中元素的特性:给定的集合,它的元素必须满足 、 、 .
2.集合相等:指构成两个集合的元素是 的.
无序性
确定性
互异性
一样
自主探究二
小试牛刀
1.组成集合的元素一定是数.( )
2.接近于0的数可以组成集合.( )
3.分别由元素0,1和1,0组成的两个集合是相等的.( )
4.一个集合中可以找到两个相同的元素.( )
×
×
×
√
自主探究三
思考:设集合A表示“1~20以内的所有质数”,那么3,4,5,6这四个元素
哪些在集合A中?哪些不在集合A中?
知识点三 元素与集合的关系
1.属于:如果a是集合A的元素,就说a 集合A,记作 .
2.不属于:如果a不是集合A中的元素,就说a 集合A,记作 .
属于
a∈A
不属于
a A
数集 非负整数集(自然数集) 正整数集 _______ 有理数集 _______
符号 ___ ________ Z ___ R
知识点四 常见的数集及表示符号
整数集
实数集
N
N*或N+
Q
N*或N+
N
Z
Q
R
小试牛刀
5.用符号“ ”或“ ”填空:
(1) 3.14_______ Q
(2) π_______ Q
(3) 0_______
(4) ____Z
N+
2
经典例题
题型一 对集合的理解
例1 (1)1.下列说法中,正确的有____.(填序号)
①中国各地的美丽乡村;
②单词book的所有字母组成的集合的元素共有4个;
③集合M中有3个元素a,b,c,其中a,b,c是△ABC的三边长,则△ABC不可能是等腰三角形;
④将小于10的自然数按从小到大的顺序排列和按从大到小的顺序排列分别得到不同的两个集合.
解析 ①中“美丽”标准不明确,不符合确定性,②不正确. book的字母o有重复,共有3个不同字母,元素个数是3.③正确. 集合M中有3个元素a,b,c,所以a,b,c都不相等,它们构成的三角形三边不相等,故不可能是等腰三角形.④不正确. 小于10的自然数不管按哪种顺序排列,里面的元素都是0,1,2,3,4,5,6,7,8,9这10个数,集合是相同的,和元素的排列顺序无关.
③
总结: 判断一组对象是否为集合的三依据
(1)确定性:负责判断这组元素是否构成集合.
(2)互异性:负责判断构成集合的元素的个数.
(3)无序性:表示只要一个集合的元素确定,则这个集合也随之确定,与元素之间的排列顺序无关.
跟踪训练
1.对于以下说法,正确的有______.(填序号)
①绝对值非常小的全体实数构成一个集合;
②长方体的全体构成一个集合;
③全体无实数根的一元二次方程构成一个集合;
④ 组成的集合含有四个元素。
解析 ①中“绝对值非常小”标准不明确,不符合确定性,②正确.③正确. ④不正确,不满足互异性
②③
题型二 元素与集合的关系
例2 下列关系中正确的个数为
A.1 B.2 C.3 D.4
√
②-1 N,②正确;
③∵π是实数,∴π∈R,故③错误;
④∵|-4|=4是整数,∴|-4|∈Z,故④正确.
总结:判断元素和集合关系的两种方法
(1)直接法:集合中的元素是直接给出的.
(2)推理法:对于某些不便直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可.
跟踪训练
2.给出下列说法:
①R中最小的元素是0;
②若a∈Z,则-a Z;
③若a∈Q,b∈N*,则a+b∈Q.
其中正确的个数为
A.0 B.1 C.2 D.3
解析 实数集中没有最小的元素,故①不正确;
对于②,若a∈Z,则-a也是整数,故-a∈Z,所以②也不正确;
只有③正确.
√
题型三 元素特性的应用
例3 (1)设集合A由元素 构成,求实数 k 的取值范围。
解 由集合中元素的互异性知
故实数k的取值范围是
题型三 元素特性的应用
例3 (2)已知集合A含有两个元素a-3和2a-1,若-3∈A,试求实数a的值.
解 ∵-3∈A, ∴-3=a-3或-3=2a-1,
①若-3=a-3,
则a=0,
此时集合A中含有两个元素-3,-1,符合题意;
②若-3=2a-1,则a=-1,
此时集合A中含有两个元素-4,-3,符合题意;
综上所述,a=0或a=-1.
总结:由集合中元素的特性求解字母取值(范围)的步骤
跟踪训练
3.(1)如果有一集合含有两个元素: ,则实数x的取值范围是________.
解 由集合中元素的互异性知 ,解得
故实数x的取值范围是
3.(2)已知集合A由元素0,m, 构成,且 2 A,求实数m的值。
解 ∵2∈A,∴m=2或 =2,
①若m=2,则 =0,不符合题意;
②若 =2,则m=0或m=3,
当m=0时,不符合题意;
当m=3时,此时集合A中含有三个元素0,3,2,符合题意;
综上所述,m=3.
跟踪训练
3
当堂达标
1.下列给出的对象中,能组成集合的是
A.一切很大的数
B.好心人
C.漂亮的小女孩
D.方程x2-1=0的实数根
√
2.下列结论不正确的是
解析 0是有理数,故0∈Q,所以C错误.
√
3.若以集合A的四个元素a,b,c,d为边长构成一个四边形,则这个四边形可能是
A.梯形 B.平行四边形
C.菱形 D.矩形
解析 由于a,b,c,d四个元素互不相同,故它们组成的四边形的四条边都不相等.
√
4.由 组成一个集合A,A中含有3个元素,则实数a的值可以是( )
A.1 B.-2 C.6 D.2
解析 由集合元素的互异性可得 ,解得a≠1,±2.
√
5.已知集合A由元素 构成,且 ,求实数a的值.
解析 ∵-3∈A,∴
①若 则a=0,此时集合A中含有三个元素-3,-1,-4,符合题意;
②若 则a=-1,此时集合A中含有元素为-4,-3,-3,不符合题意;
③若 则a =±1,由②知a=-1不符合题意,
当a=1时,此时集合A中含有三个元素-2,1,-3,符合题意;
综上所述,a=0或a=1.
6.设A是实数集,满足
(1)若 ,则集合A中至少还有几个元素?求出这几个元素。
(2)集合A中能否只含有一个元素?请说明理由。
(3)若 ,证明:
课堂小结
1.知识清单:
(1)元素与集合的概念、元素与集合的关系.
(2)常用数集的表示.
(3)集合中元素的特性及应用.
2.方法归纳:分类讨论.
3.常见误区:忽视集合中元素的互异性.
课堂作业
作业:完成对应练习
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
