人教版九年级数学上册21.3实际问题与一元二次方程(二) 课件(共20张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.3实际问题与一元二次方程(二) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 454.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 21:03:11 | ||
图片预览








文档简介
(共20张PPT)
人教版九年级数学上册课件
第二十一章 一元二次方程
实际问题与一元二次方程(二)
教学目标:
【知识与技能】
1.探索以几何图形为背景的应用题,找出其中的等量关系,建立一元二次方程,体会数学模型在解决现实生活问题中的作用.
2.能根据实际问题的意义检验结果的合理性.
【过程与方法】
经历数学建模建一元二次方程的过程,锻炼学生分析问题,解决问题的能力.
【情感态度与价值观】
通过建立一元二次方程解决实际生活问题,感受数学在生活中的实用性,提高学生学习数学的积极性,体会数学给人类生活带来的促进作用.
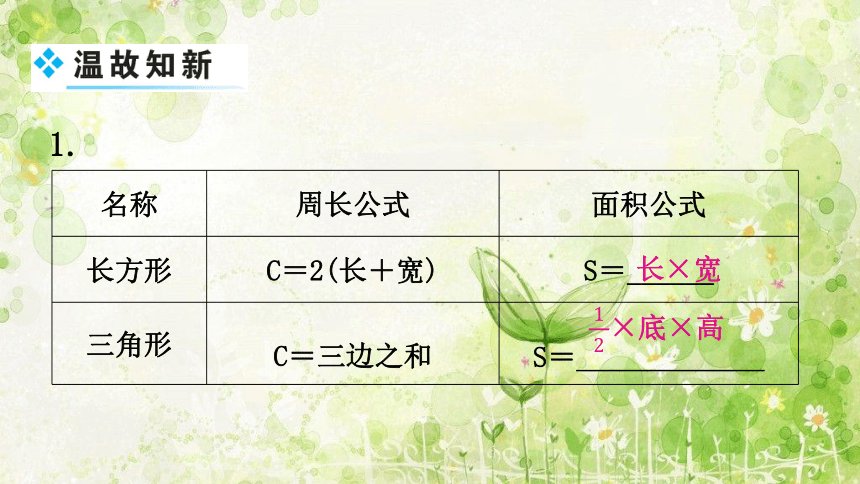
1.
名称 周长公式 面积公式
长方形 C=2(长+宽) S=______
三角形 C=三边之和 S=_____________
长×宽
×底×高
2.已知直角三角形的两条直角边长的和为7,面积为
6.设一条直角边长为x,则可得到方程_________.
3.一块面积为600 m2的长方形土地,它的长比宽多10 m,求长方形的长与宽,若设长方形的长为x m,根据题意可列方程为____________________.
x(x-10)=600
运用规则图形(矩形、三角形等)的面积公式进行求解,如果图形不规则,则先将不规则图形分割或组合成______图形,找出各部分面积的和、差关系,再用公式计算.
知识点一:面积问题
规则
4. 学校打算用长16 m的篱笆围成一个长方形的生物园饲养小动物,生物园的一面靠墙(如图21-9-1),面积是30 m2,求生物园的长和宽.设生物园的宽(与墙相邻的一边)为x m,则列出的方程为__________________.
x(16-2x)=30
明确几个名词的意义及它们之间的关系:
利润=售价-______;
利润率=×100%;
总利润=单件利润×__________.
知识点二:营销利润问题
进价
销售量
5. 某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100-x)件,商场计划要赚600元,则可列方程为_____________________.
(x-30)(100-x)=600
【例1】(RJ九上P22T9改编)某校东校区正在修建,如图21-9-2,按图纸规划,需要在一个长30 m,宽20 m的长方形ABCD空地上修建三条同样宽的通道(AB=20 m),使其中两条与AB平行,另一条与AD平行,其余部分种植草皮.要使草地
总面积为468 m2,那么通道的宽应设
计为多少米?
思路点拨:根据矩形面积公式解答即可,
巧妙地运用等积代换是解决问题的关键.
解:设通道的宽应设计为x m.根据题意,
得(30-2x)(20-x)=468.
整理,得x2-35x+66=0.
解得x1=2,x2=33(不合题意,舍去).
答:通道的宽应设计为2 m.
6. 如图21-9-3,在宽为20 m、长为30 m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551 m2,则修建的道路宽应为多少米?
解:设修建的道路宽为x m.
根据题意,得(30-x)(20-x)=551.
解得x1=49(不合题意,舍去),x2=1.
答:修建的道路宽为1 m.
【例2】某超市销售一种利润为每千克10元的水产品,一个月能销售出500 kg. 经市场分析,销售单价每涨价1元,月销售量就减少10 kg. 针对这种水产品的销售情况,若设单价每千克涨价x元,请解答以下问题:
(1)每千克水产品获利_________元,月销售量就减少________kg;
(10+x)
10x
(2)要使得月销售利润达到8 000元,又要“薄利多销”,销售单价应涨价多少元?
思路点拨:(1)根据已知条件可直接用x表示出所要求的量;
(2)利用每千克水产品获利×月销售量=总利润,列方程求解即可.
解:(2)由题意,得(10+x)(500-10x)=8 000.
解得x1=10,x2=30.
∵要“薄利多销”,
∴x=10.
答:销售单价应涨价10元.
7. 一商店销售某种商品,平均每天可售出40件,每件盈利40元,为了扩大销售同时增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出5件.
(1)若销售单价降低m元,则平均每天销售数量为__________件,每件盈利_________元;
(40+5m)
(40-m)
(2)当每件商品降价多少元时,该商店每天销售利润为2 800元?
解:(2)由题意,得(40+5m)(40-m)=2 800.
解得m1=20,m2=12.
∵40-m≥25,∴m≤15. ∴m=12.
答:当每件商品降价12元时,该商店每天销售利润为2 800元.
小结:通过这节课的学习,谈谈你对列一元二次方程解决实际
问题的体会和收获?你认为有哪些地方需要特别注意?
(让学生回顾整理本节知识,反思学习过程的体会,加深理解.)
教学反思:
1.面积问题的设置,力求以点带面,了解列一元二次方程的步骤并能解答简单的应用题,训练题是对前面问题的延伸,使学生灵活运用解题的能力有很大的提高,对学生思维能力的拓展、发散有很大的帮助.
2.列一元二次方程解应用题是让数学来源于生活,是对一元二次方程解法的延伸,同时又是一元二次方程或二元一次方程组解应用题步骤的总结和内容的升华,列一元二次方程解应用题是下章中学习二次函数解决问题的基础.
谢 谢
人教版九年级数学上册课件
第二十一章 一元二次方程
实际问题与一元二次方程(二)
教学目标:
【知识与技能】
1.探索以几何图形为背景的应用题,找出其中的等量关系,建立一元二次方程,体会数学模型在解决现实生活问题中的作用.
2.能根据实际问题的意义检验结果的合理性.
【过程与方法】
经历数学建模建一元二次方程的过程,锻炼学生分析问题,解决问题的能力.
【情感态度与价值观】
通过建立一元二次方程解决实际生活问题,感受数学在生活中的实用性,提高学生学习数学的积极性,体会数学给人类生活带来的促进作用.
1.
名称 周长公式 面积公式
长方形 C=2(长+宽) S=______
三角形 C=三边之和 S=_____________
长×宽
×底×高
2.已知直角三角形的两条直角边长的和为7,面积为
6.设一条直角边长为x,则可得到方程_________.
3.一块面积为600 m2的长方形土地,它的长比宽多10 m,求长方形的长与宽,若设长方形的长为x m,根据题意可列方程为____________________.
x(x-10)=600
运用规则图形(矩形、三角形等)的面积公式进行求解,如果图形不规则,则先将不规则图形分割或组合成______图形,找出各部分面积的和、差关系,再用公式计算.
知识点一:面积问题
规则
4. 学校打算用长16 m的篱笆围成一个长方形的生物园饲养小动物,生物园的一面靠墙(如图21-9-1),面积是30 m2,求生物园的长和宽.设生物园的宽(与墙相邻的一边)为x m,则列出的方程为__________________.
x(16-2x)=30
明确几个名词的意义及它们之间的关系:
利润=售价-______;
利润率=×100%;
总利润=单件利润×__________.
知识点二:营销利润问题
进价
销售量
5. 某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100-x)件,商场计划要赚600元,则可列方程为_____________________.
(x-30)(100-x)=600
【例1】(RJ九上P22T9改编)某校东校区正在修建,如图21-9-2,按图纸规划,需要在一个长30 m,宽20 m的长方形ABCD空地上修建三条同样宽的通道(AB=20 m),使其中两条与AB平行,另一条与AD平行,其余部分种植草皮.要使草地
总面积为468 m2,那么通道的宽应设
计为多少米?
思路点拨:根据矩形面积公式解答即可,
巧妙地运用等积代换是解决问题的关键.
解:设通道的宽应设计为x m.根据题意,
得(30-2x)(20-x)=468.
整理,得x2-35x+66=0.
解得x1=2,x2=33(不合题意,舍去).
答:通道的宽应设计为2 m.
6. 如图21-9-3,在宽为20 m、长为30 m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551 m2,则修建的道路宽应为多少米?
解:设修建的道路宽为x m.
根据题意,得(30-x)(20-x)=551.
解得x1=49(不合题意,舍去),x2=1.
答:修建的道路宽为1 m.
【例2】某超市销售一种利润为每千克10元的水产品,一个月能销售出500 kg. 经市场分析,销售单价每涨价1元,月销售量就减少10 kg. 针对这种水产品的销售情况,若设单价每千克涨价x元,请解答以下问题:
(1)每千克水产品获利_________元,月销售量就减少________kg;
(10+x)
10x
(2)要使得月销售利润达到8 000元,又要“薄利多销”,销售单价应涨价多少元?
思路点拨:(1)根据已知条件可直接用x表示出所要求的量;
(2)利用每千克水产品获利×月销售量=总利润,列方程求解即可.
解:(2)由题意,得(10+x)(500-10x)=8 000.
解得x1=10,x2=30.
∵要“薄利多销”,
∴x=10.
答:销售单价应涨价10元.
7. 一商店销售某种商品,平均每天可售出40件,每件盈利40元,为了扩大销售同时增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出5件.
(1)若销售单价降低m元,则平均每天销售数量为__________件,每件盈利_________元;
(40+5m)
(40-m)
(2)当每件商品降价多少元时,该商店每天销售利润为2 800元?
解:(2)由题意,得(40+5m)(40-m)=2 800.
解得m1=20,m2=12.
∵40-m≥25,∴m≤15. ∴m=12.
答:当每件商品降价12元时,该商店每天销售利润为2 800元.
小结:通过这节课的学习,谈谈你对列一元二次方程解决实际
问题的体会和收获?你认为有哪些地方需要特别注意?
(让学生回顾整理本节知识,反思学习过程的体会,加深理解.)
教学反思:
1.面积问题的设置,力求以点带面,了解列一元二次方程的步骤并能解答简单的应用题,训练题是对前面问题的延伸,使学生灵活运用解题的能力有很大的提高,对学生思维能力的拓展、发散有很大的帮助.
2.列一元二次方程解应用题是让数学来源于生活,是对一元二次方程解法的延伸,同时又是一元二次方程或二元一次方程组解应用题步骤的总结和内容的升华,列一元二次方程解应用题是下章中学习二次函数解决问题的基础.
谢 谢
同课章节目录
