图形的初步认识（复习课）[上学期]

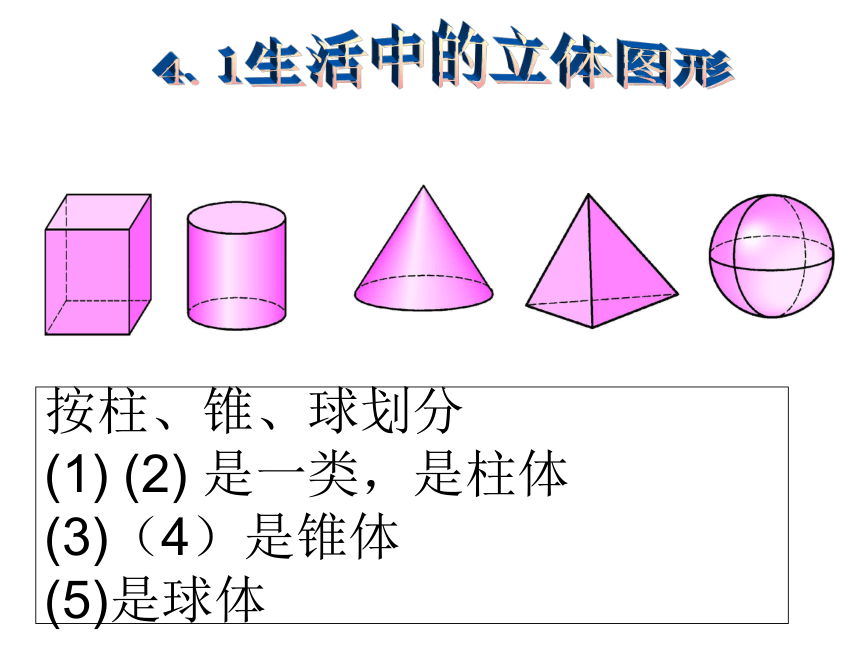
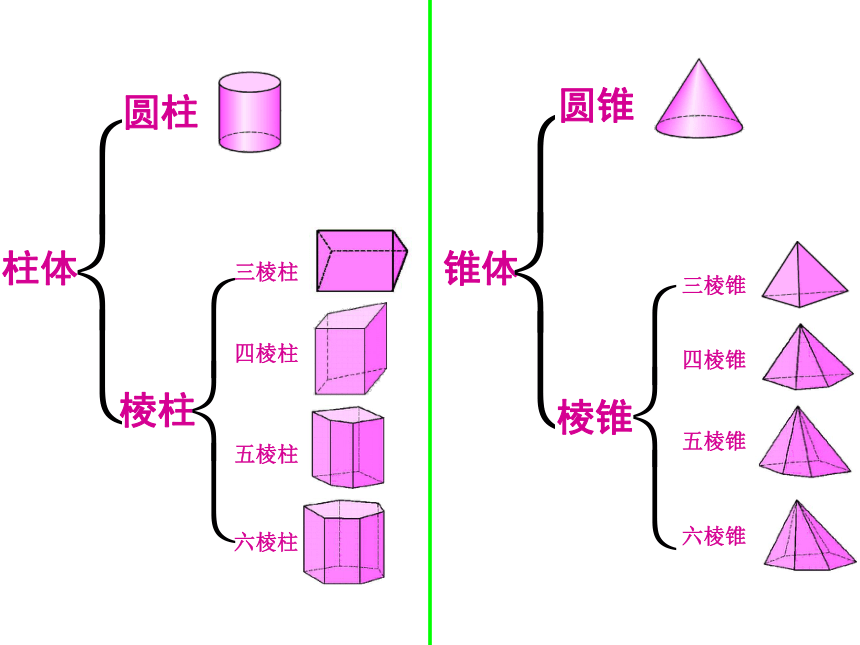
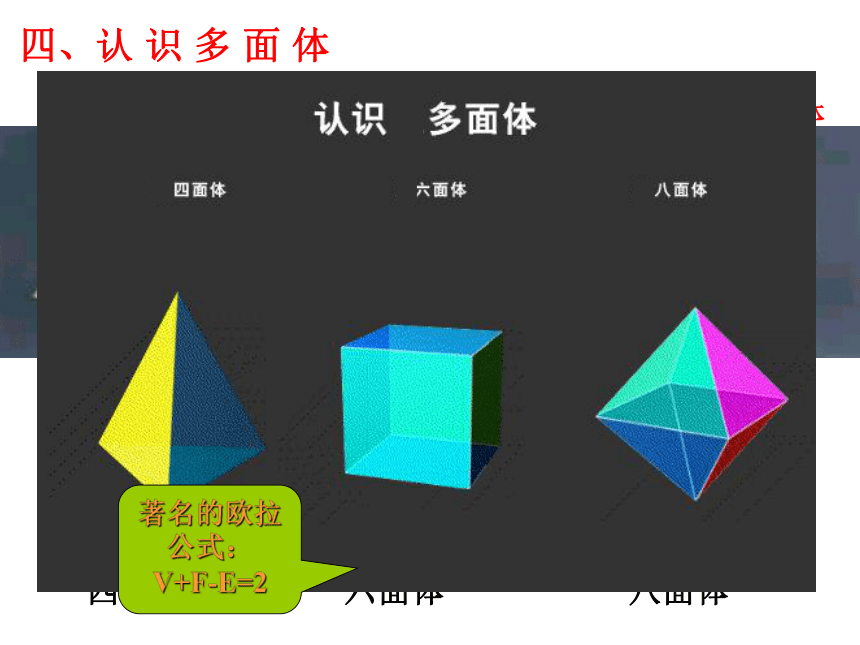
课件28张PPT。第四章 图形的初步认识（复习课）4.1生活中的立体图形按柱、锥、球划分(1) (2) 是一类，是柱体(3)（4）是锥体 (5)是球体柱体锥体圆柱棱柱圆锥棱锥四面体六面体八面体多面体可以按面数来分类，如下列图形中： 若围成立体图形的面是平的面，这样的立体图形又称为多面体四、认 识 多 面 体著名的欧拉公式：
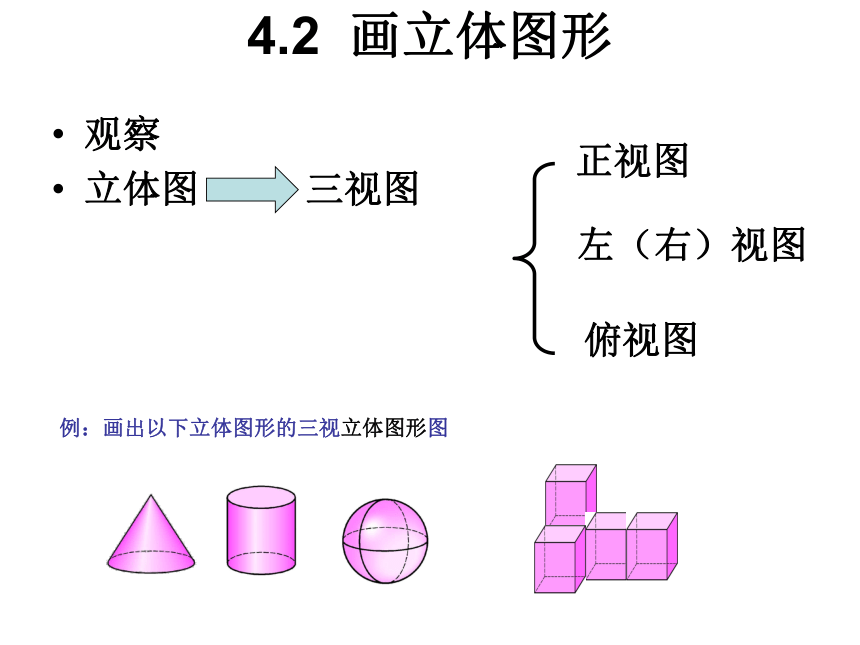
V+F-E=24.2 画立体图形观察
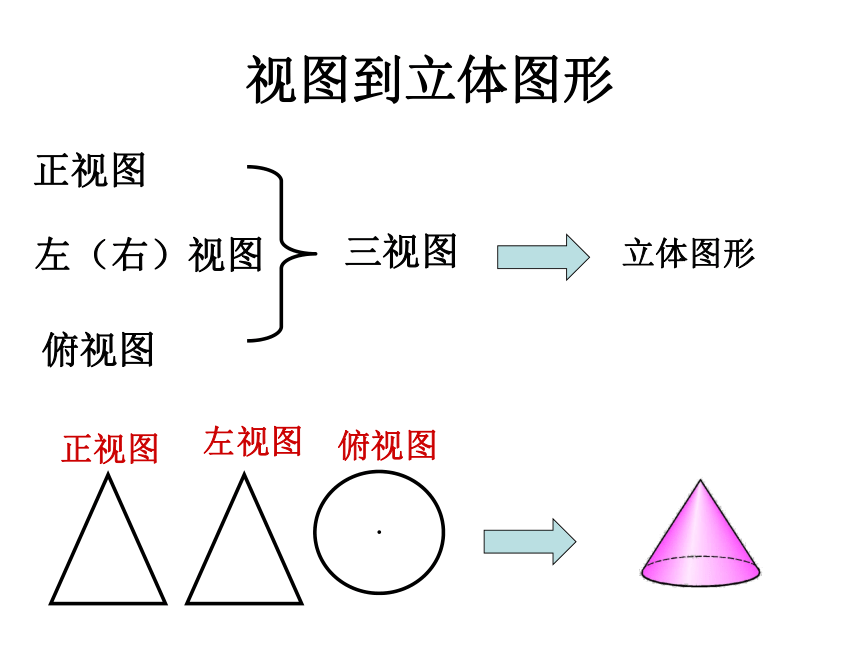
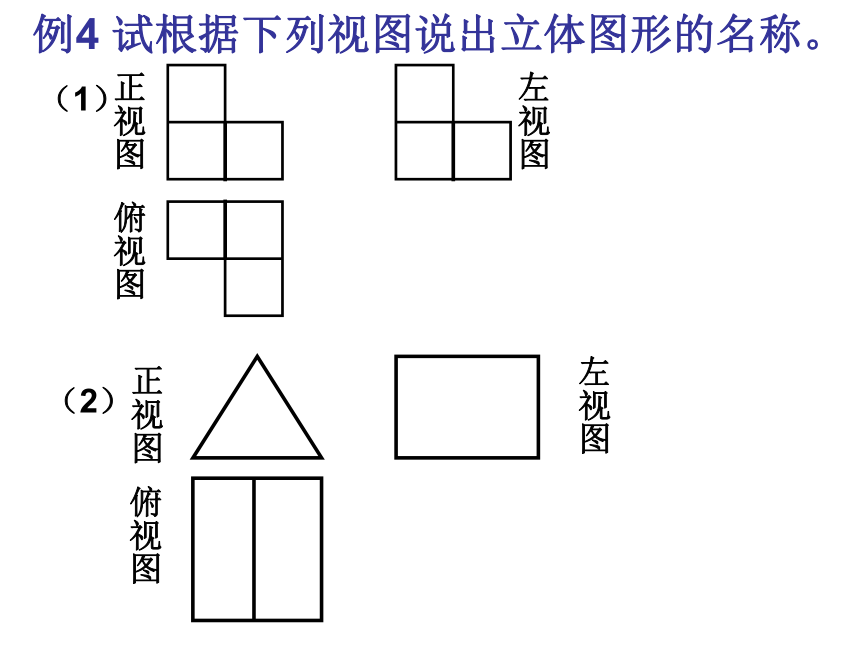
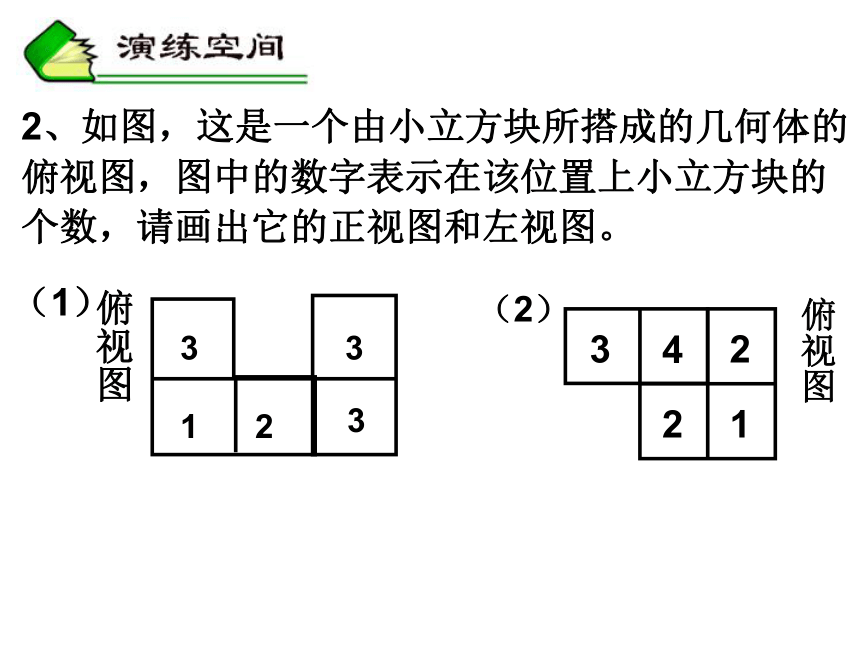
立体图 三视图正视图左（右）视图俯视图例：画出以下立体图形的三视立体图形图视图到立体图形正视图左（右）视图俯视图三视图立体图形例4 试根据下列视图说出立体图形的名称。正视图左视图俯视图（1）2、如图，这是一个由小立方块所搭成的几何体的
俯视图，图中的数字表示在该位置上小立方块的
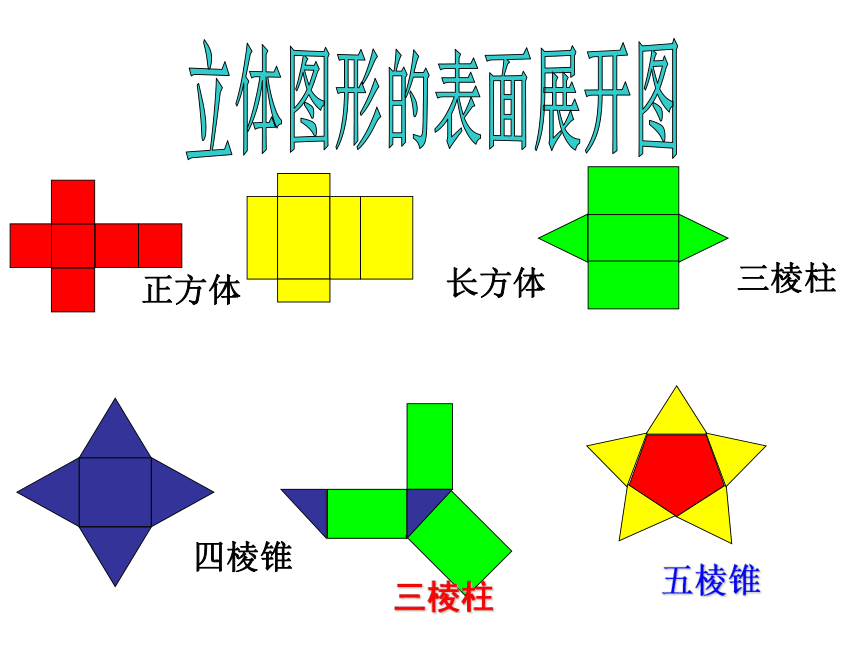
个数，请画出它的正视图和左视图。立体图形的表面展开图正方体长方体四棱锥三棱柱三棱柱五棱锥 归纳：正方体
的表面展开图
有以下11种。你能看
出有什么规律吗？4.4 平面图形什么叫多边形
每个多边形可以分割（ ）不重合的三角形。
多边形的内角和公式：线段封闭N-24.5 点和线A 点A ——用一个大写字母表示。 线线段直线射线学会区分没有4.5线段的长短比较1 度量法2 叠合法3 线段中点的定义和简单作法。1 度量法4.6 角用一个大写字母表示点，用二个大写字母表示线，用三个大写字母表示角，
角度的转化：
1°=60′ ，1′=60” 1°=3600 ”
角度的加减：
1.同种形式相加减；
2.度加（减）度；分加（减）分；秒加（减）秒
3.超60进一；减一成60
4.4 角的比较2 叠合法1 度量法∠ABC=∠DEF∠ABC<∠DEF∠ABC>∠DEF角的平分线2、几何语言表达：∵ OC是∠AOB的平分线OABC12∴∠1＝∠2＝ ∠AOB
或∠AOB＝２∠１＝２∠２1角的平分线1、定义：一条射线把一个角分成两个相等
的角， 这条射线叫做这个角的平分线． 2、几何语言表达：∵ OC是∠AOB的平分线OABC12∴∠1＝∠2＝ ∠AOB
或∠AOB＝２∠１＝２∠２1角的特殊关系 2、∠１与∠２互补，∠１是∠２的补角，∠２是∠１的补角．∠１＋∠２＝18０ °1、∠１与∠２互余，∠１是∠２的余角，∠２是∠１的余角．∠１＋∠２＝９０ °１）两个角成对出现２）只考虑数量关系，与位置无关．结论: 同角(等角)的补角相等 注意!判断下列各图中的∠1和∠2是不是对顶角。
结论: 对顶角相等4.7 相交线—垂线 记作“AB⊥CD”，垂足为点O。读作“AB垂直于CD”或“CD垂直于AB”。垂直的定义：请同学们用三角尺或量角器作为工具：
　　（1）经过直线AB外一点P，画直线与已知直线AB垂直，2．在如图所示的各个三角形中，分别画出AB边上的高，并量出三角形顶点C到直线AB的距离。┓ ┓ ┓ 4.7 相交线 ----相交线中的角三线八角图找角步骤：1、找三线、截线。1、找角：laP124b56783Q你还记得怎样用移动三角尺的方法画两条平行线吗？一、放二、泊三、移四、画2.内错角相等，两直线平行。∴ AB∥CD（内错角相等，两直线平行）∵ ∠1= ∠2∴ AB∥CD （同旁内角互补，两直线平行）3.同旁内角互补，两直线平行。∵ ∠1+∠2=180 °两直线平行 同位角相等内错角相等同旁内角互补平行线的识别平行线的特征线的关系角的关系特征角的关系线的关系识别同位角相等，两直线平行。∴ AB∥CD
（同位角相等，两直线平行）∵ ∠1 = ∠212aABCD两直线平行，同位角相等。∴ ∠1 = ∠2
（两直线平行，同位角相等。）∵ AB∥CD
画出将如图所示的方格纸中的图形向
右平移3格，并向下平移4格后的图形。