人教版七年级数学下册8.3 实际问题与二元一次方程组 工程问题 课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学下册8.3 实际问题与二元一次方程组 工程问题 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 359.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 22:40:49 | ||
图片预览







文档简介
(共20张PPT)
二元一次方程组的神奇
——行程问题
知识回顾
1 列方程解决问题的一般步骤是什么?
设 找 列 解 验 答
2 列二元一次方程组关键是什么?
根据题意找出题目中的两个等量关系!
3 常见的行程问题有哪些?
学习内容
二元一次方程与行程问题.
1)相遇问题
2)追及问题
3)环形跑道问题
4)错车问题
5)航行问题
6)火车过桥问题
7)上、下坡问题
行程问题
回顾与行程有关的三个量之间的关系
路程=速度×时间
行程问题-相遇问题
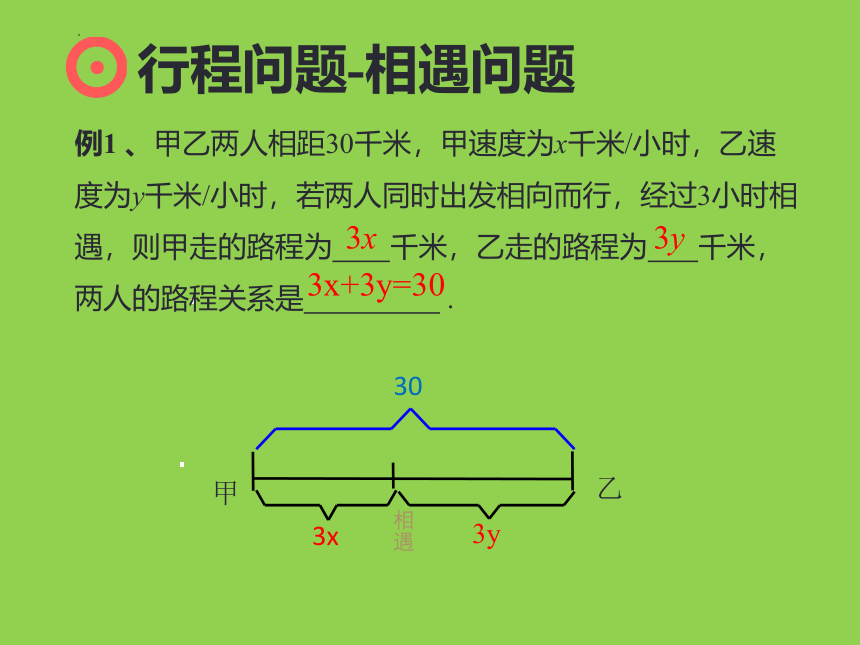
例1 、甲乙两人相距30千米,甲速度为x千米/小时,乙速度为y千米/小时,若两人同时出发相向而行,经过3小时相遇,则甲走的路程为 千米,乙走的路程为 千米,两人的路程关系是 .
甲
乙
3y
3x
相遇
30
3x
3y
3x+3y=30
关键词:相向、相对、相遇
甲走的路程 + 乙走的路程 = 总路程
行程问题-相遇问题
变式1、甲、乙两人骑车从相距38千米的两地相向出发,在甲走了1.5小时,乙走了2小时后相遇,第二次他们同时从两地相向出发,经过1小时15分钟,两人还相距10.5千米,求甲、乙两人骑车的速度.
行程问题-相遇问题
行程问题-追及问题
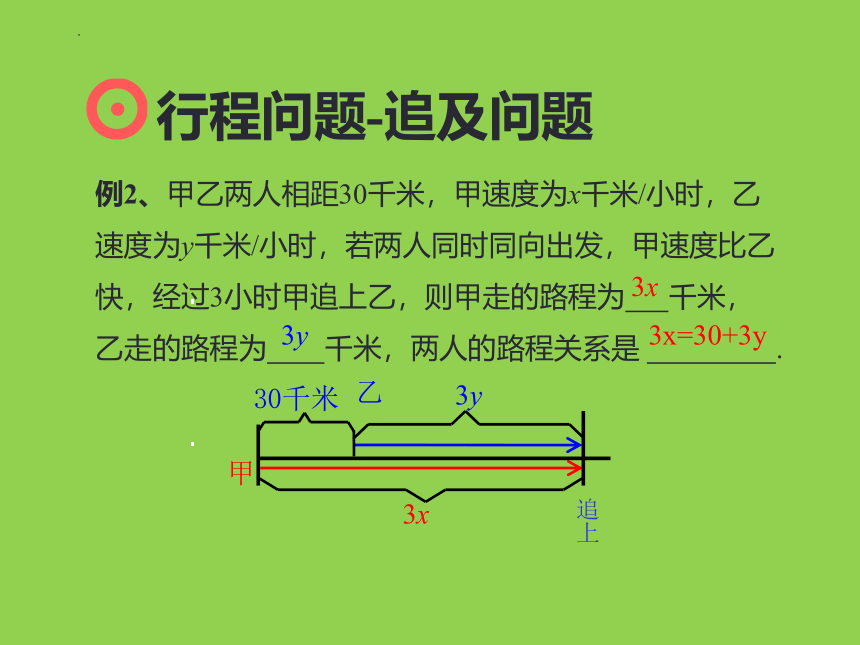
例2、甲乙两人相距30千米,甲速度为x千米/小时,乙速度为y千米/小时,若两人同时同向出发,甲速度比乙快,经过3小时甲追上乙,则甲走的路程为 千米,乙走的路程为 千米,两人的路程关系是 .
追上
3y
甲
乙
3x
30千米
3y
3x
3x=30+3y
行程问题-追及问题
关键词:同向、追上
快的路程-慢的路程 = 原距离
变式2、A、B 两地相距20千米,甲、乙两人分别从A、B两地同时相向而行,2小时后在途中相遇,然后甲返回A地,乙继续前进,当甲返回到A地时,乙离A地还有2千米.求甲、乙两人的速度各是多少?
行程问题-追及问题
例3、甲、乙两人在400米的环形跑道上练习赛跑,如果两人同时同地反向跑,经过25秒第一次相遇;如果两人同时同地同向跑,经过200秒甲第一次追上乙.求甲、乙两人的平均速度.
行程问题-环形跑道问题
行程问题-环形跑道问题
关键词:环形、相遇、追上
同向:快的路程-慢的路程 = 环形跑道长度
反向:快的路程 + 慢的路程 = 环形跑道长度
变式3、两人骑自行车在400米环形跑道上用不变的速度行驶,当他们按相反的方向行驶时每20秒名相遇一次;若按同一方向行驶,那么每100秒钟相遇一次,问两个的速度各是多少?
行程问题-环形跑道问题
错车过程中的行程问题
例4.、一列快车长230米,一列慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟;若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟,问快车和慢车的速度各是多少?
解答:设快车、慢车的速度分别为x m/s、y m/s
得 90(x-y)=450
同向情况:快车长230米,慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟
230m
甲
220m
乙
220m
乙
230m
甲
S慢
S快
得 18(x+y)=450
相向情况:若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟
解之得
x=15
y=10
90(x-y)=450
18(x+y)=450
230m
甲
220m
乙
230m
甲
220m
乙
S慢
S快
230+220
关键词:错车
同向:快车的路程 – 慢车的路程 = 快车长度+慢车长度
反向:快车的路程 + 慢车的路程 = 快车长度+慢车长度
错车过程中的行程问题
变式4、客车和火车分别在两条互相平行的铁轨上行驶,客车长150米,火车长250米.如果两车相向而行,那么从两车车头相遇到车尾离开共需10秒钟;如果客车从后面追火车,那么从客车车头追上火车车尾到客车车尾离开火车车头共需1分40秒.求两车的速度.
今日思考
某人沿公路匀速前进,每隔4min就遇到迎面开来的一辆公共汽车,每隔6min就有一辆公共汽车从背后超过他.假定汽车速度不变,而且迎面开来相邻两车的距离和从背后开来相邻两车的距离都是1200m,求某人前进的速度和公共汽车的速度,汽车每隔几分钟开出一辆?
总结
今天学习的知识点有哪些呢?
二元一次方程组的神奇
——行程问题
知识回顾
1 列方程解决问题的一般步骤是什么?
设 找 列 解 验 答
2 列二元一次方程组关键是什么?
根据题意找出题目中的两个等量关系!
3 常见的行程问题有哪些?
学习内容
二元一次方程与行程问题.
1)相遇问题
2)追及问题
3)环形跑道问题
4)错车问题
5)航行问题
6)火车过桥问题
7)上、下坡问题
行程问题
回顾与行程有关的三个量之间的关系
路程=速度×时间
行程问题-相遇问题
例1 、甲乙两人相距30千米,甲速度为x千米/小时,乙速度为y千米/小时,若两人同时出发相向而行,经过3小时相遇,则甲走的路程为 千米,乙走的路程为 千米,两人的路程关系是 .
甲
乙
3y
3x
相遇
30
3x
3y
3x+3y=30
关键词:相向、相对、相遇
甲走的路程 + 乙走的路程 = 总路程
行程问题-相遇问题
变式1、甲、乙两人骑车从相距38千米的两地相向出发,在甲走了1.5小时,乙走了2小时后相遇,第二次他们同时从两地相向出发,经过1小时15分钟,两人还相距10.5千米,求甲、乙两人骑车的速度.
行程问题-相遇问题
行程问题-追及问题
例2、甲乙两人相距30千米,甲速度为x千米/小时,乙速度为y千米/小时,若两人同时同向出发,甲速度比乙快,经过3小时甲追上乙,则甲走的路程为 千米,乙走的路程为 千米,两人的路程关系是 .
追上
3y
甲
乙
3x
30千米
3y
3x
3x=30+3y
行程问题-追及问题
关键词:同向、追上
快的路程-慢的路程 = 原距离
变式2、A、B 两地相距20千米,甲、乙两人分别从A、B两地同时相向而行,2小时后在途中相遇,然后甲返回A地,乙继续前进,当甲返回到A地时,乙离A地还有2千米.求甲、乙两人的速度各是多少?
行程问题-追及问题
例3、甲、乙两人在400米的环形跑道上练习赛跑,如果两人同时同地反向跑,经过25秒第一次相遇;如果两人同时同地同向跑,经过200秒甲第一次追上乙.求甲、乙两人的平均速度.
行程问题-环形跑道问题
行程问题-环形跑道问题
关键词:环形、相遇、追上
同向:快的路程-慢的路程 = 环形跑道长度
反向:快的路程 + 慢的路程 = 环形跑道长度
变式3、两人骑自行车在400米环形跑道上用不变的速度行驶,当他们按相反的方向行驶时每20秒名相遇一次;若按同一方向行驶,那么每100秒钟相遇一次,问两个的速度各是多少?
行程问题-环形跑道问题
错车过程中的行程问题
例4.、一列快车长230米,一列慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟;若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟,问快车和慢车的速度各是多少?
解答:设快车、慢车的速度分别为x m/s、y m/s
得 90(x-y)=450
同向情况:快车长230米,慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟
230m
甲
220m
乙
220m
乙
230m
甲
S慢
S快
得 18(x+y)=450
相向情况:若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟
解之得
x=15
y=10
90(x-y)=450
18(x+y)=450
230m
甲
220m
乙
230m
甲
220m
乙
S慢
S快
230+220
关键词:错车
同向:快车的路程 – 慢车的路程 = 快车长度+慢车长度
反向:快车的路程 + 慢车的路程 = 快车长度+慢车长度
错车过程中的行程问题
变式4、客车和火车分别在两条互相平行的铁轨上行驶,客车长150米,火车长250米.如果两车相向而行,那么从两车车头相遇到车尾离开共需10秒钟;如果客车从后面追火车,那么从客车车头追上火车车尾到客车车尾离开火车车头共需1分40秒.求两车的速度.
今日思考
某人沿公路匀速前进,每隔4min就遇到迎面开来的一辆公共汽车,每隔6min就有一辆公共汽车从背后超过他.假定汽车速度不变,而且迎面开来相邻两车的距离和从背后开来相邻两车的距离都是1200m,求某人前进的速度和公共汽车的速度,汽车每隔几分钟开出一辆?
总结
今天学习的知识点有哪些呢?
