辽宁省锦州市2022-2023学年高二下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 辽宁省锦州市2022-2023学年高二下学期期末考试数学试题(Word版含答案) | 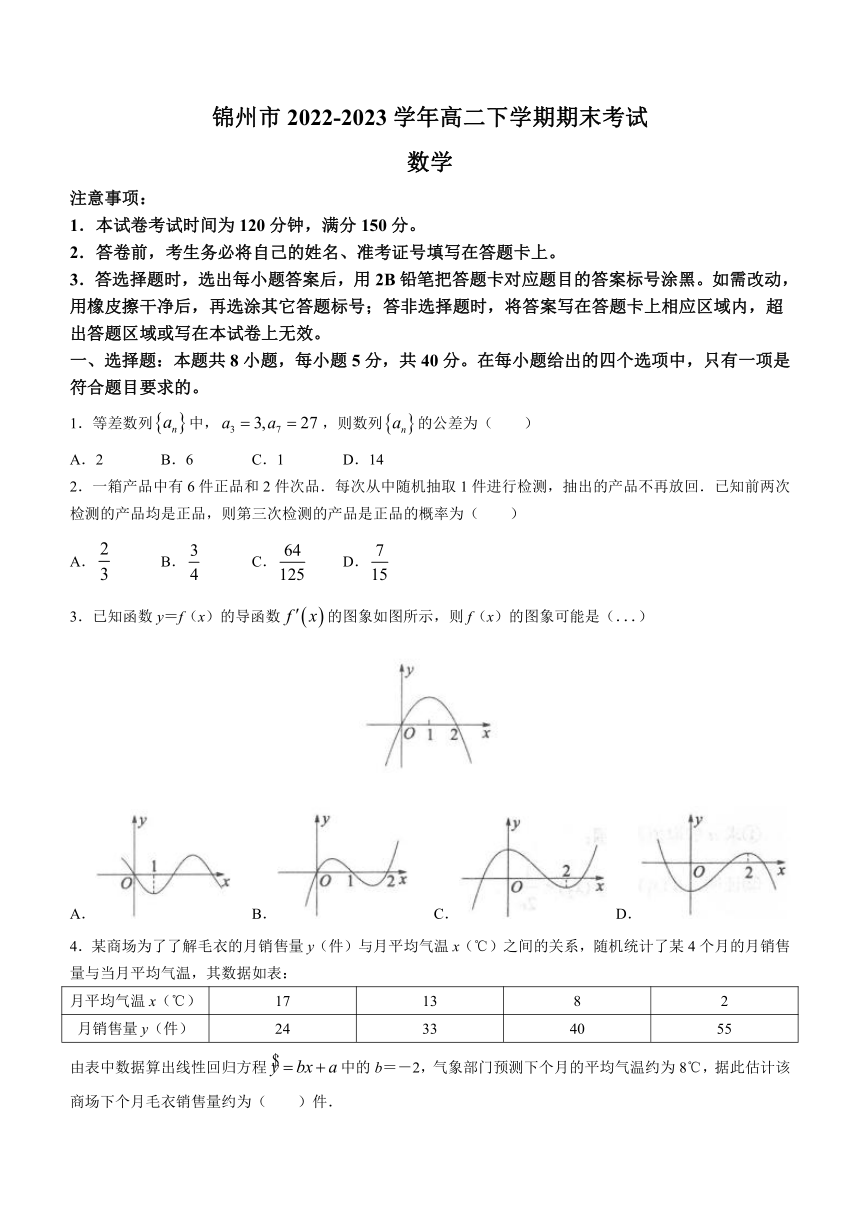 | |
| 格式 | docx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 12:18:23 | ||
图片预览





文档简介
锦州市2022-2023学年高二下学期期末考试
数学
注意事项:
1.本试卷考试时间为120分钟,满分150分。
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3.答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答题标号;答非选择题时,将答案写在答题卡上相应区域内,超出答题区域或写在本试卷上无效。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.等差数列中,,则数列的公差为( )
A.2 B.6 C.1 D.14
2.一箱产品中有6件正品和2件次品.每次从中随机抽取1件进行检测,抽出的产品不再放回.已知前两次检测的产品均是正品,则第三次检测的产品是正品的概率为( )
A. B. C. D.
3.已知函数y=f(x)的导函数的图象如图所示,则f(x)的图象可能是(...)
A. B. C. D.
4.某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
由表中数据算出线性回归方程中的b=-2,气象部门预测下个月的平均气温约为8℃,据此估计该商场下个月毛衣销售量约为( )件.
A.40 B.42 C.46. D.48
5.康托(Cantor)是十九世纪末二十世纪初德国伟大的数学家,他创立的集合论奠定了现代数学的基础.著名的“康托三分集”是数学理性思维的产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段,当记为第一次操作;再将剩下的两个区间分别均分为三段,并各自去掉中间的区间段,记为第二次操作:…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使“康托三分集”的各区间长度之和小于,则需要操作的次数n的最小值为( )(参考数据:)
A.6 B.8 C.10 D.12
6.已知,设曲线在x=k(k>0)处的切线斜率为f(k),则( )
A.f(c)<f(b)<f(a) B.f(a)<f(c)<f(b)
C.f(c)<f(a)<f(b) D.f(a)<f(b)<f(c)
7.某班举行航空知识闯关活动,共设置A,B,C三个问题.答题者可自行决定答三道题的顺序.甲有60%的可能答对问题A,80%的可能答对问题B,50%的可能答对问题C.记答题者连续答对两题的概率为p,要使得p最大,他应该先回答( )
A.问题A B.问题B C.问题C D.问题A,B和C都可以
8.若过点P(t,0)可以作曲线y=(1-x)ex的两条切线,切点分别为,则的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分有选错的得0分。
9.已知5个成对数据(x,y)的散点图如下,且y与x线性相关,若去掉点D(4,3),则下列说法正确的是( )
A.变量x与变量y呈负相关.
B.变量x与变量y的线性相关关系变强
C.残差平方和变小
D.样本相关系数r变大
10.已知递减的等差数列的前n项和为,则( )
A. B. C. D.最大
11.已知函数,则( )
A.f(x)有一个零点 B.f(x)在上单调递减
C.f(x)有一个极值点 D.若,则
12.一种疾病需要通过核酸检测来确定是否患病,检测结果呈阴性即没患病,呈阳性即为患病,已知7人中有1人患有这种疾病,先任取4人,将他们的核酸采样混在一起检测.若结果呈阳性,则表明患病者为这4人中的1人,然后再逐个检测,直到能确定患病者为止;若结果呈阴性,则在另外3人中逐个检测,直到能确定患病者为止,则( )
A.最多需要检测4次可确定患病者 B.第2次检测后就可确定患病者的概率为
C.第3次检测后就可确定患病者的概率为 D.检测次数的期望为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数,则______.
14.某城市每年6月份的平均气温t近似服从,若,则可估计该城市6月份平均气温低于24摄氏度的天数为______.
15.设口袋中有白球3个,黑球若干个,从中任取2个球,设抽到的球中白球个数为x个,且,则口袋中共有黑球______个.
16.已知函数,则______;设数列满足,则此数列的前2023项的和为______.
四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知数列满足.
(1)证明:是等比数列;
(2)证明:存在两个等比数列,使得成立.
18.(本题满分12分)
已知函数.
(1)若x=1是函数f(x)的极小值点,求a的值;
(2)讨论f(x)的单调性.
19.(本题满分12分)
青少年时期是视觉发育的敏感期与关键期,这个阶段的视觉发育容易受环境因素影响,某校为研究学生每天使用手机时长与近视率的关系,从全校学生中随机抽取600名学生进行不记名问卷调查,得到如下数据:有20%的学生每天使用手机超过1h,这些人的近视率为50%;每天使用手机不超过1h的学生的近视率为37.5%.
(1)若从该校学生中随机抽取一人,请根据以上数据估计该同学近视的概率;
(2)请完成2×2列联表.并根据调查数据回答:在犯错误的概率不超过5%的前提下.可以认为该校学生每天使用手机时长与近视有关吗?
视力 每天使用手机时长 合计
超过1h 不超过1h
近视
不近视
合计 600
附:.
下表是独立性检验中几个常用的小概率值和相应的临界值:
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
20.(本题满分12分)
已知等比数列的公比q>0,且满足,数列的前n项和.
(1)求数列和的通项公式;
(2)设,求数列的前2n项和.
21.(本题满分12分)
某商场为庆祝六一儿童节,举办了一场赢取小熊挂件的“定点投篮”活动,方案如下:
方案一:共投9次,每次投中得1分,否则得0分,累计所得分数记为Y;
方案二:共进行三轮投篮,每轮最多投三次,直到投中两球为止得3分,否则得0分,三轮累计所得分数记为X.
累计所得分数越多,所获得奖品越多.现在甲准备参加这个“定点投篮”活动,已知甲每次投篮的命中率为p(0<p<1),每次投篮互不影响.
(1)若,甲选择方案二,求第一轮投篮结束时,甲得3分的概率;
(2)以最终累计得分的期望值为决策依据,甲在方案一,方案二之中选其一,应选择哪个方案?
22.(本题满分12分)
已知函数.
(1)若a=2,求方程f(x)=0的解集;
(2)若f(x)有两个零点且有两个极值点,记两个极值点为,
①求a的取值范围;
②证明:.
2022~2023学年度第二学期期末考试
高二数学(参考答案及评分标准)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有-项是符合题目要求的。
BADB BACD
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.ABC. 10.ACD. 11.BCD. 12.AB.
三、填空题:本题共4小题,每小题5分,共20分.
13.6. 14.9. 15.4 16.;.(第一空2分,第二空3分)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
证明:(1)因为,所以,
又,数列是首项为3,公比为3的等比数列.
(2)存在两个等比数列,使得成立.
理由如下:由(1)知,.
所以,
因为,所以数列是首项为-2,公比为2的等比数列,
所以.所以.
令,则,
所以,存在两个等比数列,使得成立.
18.(本题满分12分)
解:(1)
令,得:,
由于x=1是函数f(x)的极小值点,所以,即a=1,
此时因为x∈(-∞,0)时,,f(x)在(-∞,0)上单调递增,
x∈(0,1)时,,f(x)在(0,1)上单调递减,
x∈(1,+∞)时,,f(x)在(1,+∞)上单调递增,
所以x=1是函数f(x)的极小值点,故a=1满足题意.
(2)时x=0或x=a,
a<0时,的解为x<a或x>0,此时f(x)在(-∞,a]和[0,+∞)上单调递增;
的解为a<x<0,此时f(x)在[a,0]上单调递减;
a>0时,的解为x<0或x>a,此时f(x)在(-∞,0]和[(a,+∞)上单调递增;
的解为0<x<a,此时f(x)在[0,a]上单调递减;
a=0时,恒成立,此时f(x)在R上单调递增.
19.(本题满分12分)
解:(1)设事件A为“任选1名学生每天使用手机超过1h”,事件B为“任选1名学生近视”,则,
由全概率公式得,
所以从该校学生中随机抽取一名学生其近视的概率为0.4.
(2)2×2列联表为
视力 每天使用手机时长 合计
超过1h 不超过1h
近视 60 180 240
不近视 60 300 360
合计 120 480 600
根据列联表中的数据,经计算得到,
所以在犯错误的概率不超过5%的前提下.可以认为该校学生每天使用手机时长与近视有关联.
20.(本题满分12分)
解:(1)依题意,由,可得
,解得,
所以,
因为数列的前n项和,所以当n=1时,,
当n≥2时,,
也满足上式,所以.
(2)由题意及(1),可知
当n为奇数时,,
当n为偶数时,,
令,则
,
,
所以,
两式相减,可得:
,
,
,
所以,
所以
.
21.(本题满分12分)
解:(1)设事件A为“甲3次投篮,前两球投进”;事件B为“甲3次投篮,最后一次才投进第2球”,则甲得3分为这两个事件的和事件,
所以,
所以第一轮投篮结束时,甲得3分的概率;
(2)选方案一,则,选方案一得分的数学期望为E(Y)=9p,
选方案二,每一轮得分只有0和3,能得3分的概率为
,
进行三轮投篮,得3分的次数ξ为随机变量,则,
进行三轮总得分X=3ξ,则选择方案二得分的期望为
,
所以,
当,两种方案期望相同,所以选方案一,二都可以,
当,方案二期望大,所以甲应该选方案二,
当,方案一期望大,所以甲应该选方案一.
22.(本题满分12分)
(1)解:若a=2,则,定义域为(0,+∞),
由f(x)=0,可得x-1-lnx=0,
设g(x)=x-1-lnx,则,
由,可得0<x<1,g(x)在(0,1)上单调递减,
由,可得x>1,g(x)在(1,+∞)上单调递增,
所以,
故方程f(x)=0的解集为.
(2)①解:令f(x)=0,得,设,
由,可得0<x<1,故h(x)在(0,1)单调递增;
由,可得x>1,故h(x)在(1,+∞)单调递减,所以,
又当x∈(0,1)时,,当时,h(x)∈(0,1),
若f(x)有两个零点,则,故a∈(0,2),
,令,得,
设,则,由,可得,
由,可得,故H(x)在上单调递增;
由,可得,故H(x)在上单调递减,,
当时,,当时,,
若f(x)有两个极值点,则a∈(0,e),
综上,a∈(0,2),
②证明:不妨令,因为且H(1)=2,得,
由为的两根得,
两式分别乘并整理得:
,
所以,
要证:,即证:,
即证:,
由于,所以,
所以只需证,
令,
,所以在上单调递减,
所以,故,
所以.
数学
注意事项:
1.本试卷考试时间为120分钟,满分150分。
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3.答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答题标号;答非选择题时,将答案写在答题卡上相应区域内,超出答题区域或写在本试卷上无效。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.等差数列中,,则数列的公差为( )
A.2 B.6 C.1 D.14
2.一箱产品中有6件正品和2件次品.每次从中随机抽取1件进行检测,抽出的产品不再放回.已知前两次检测的产品均是正品,则第三次检测的产品是正品的概率为( )
A. B. C. D.
3.已知函数y=f(x)的导函数的图象如图所示,则f(x)的图象可能是(...)
A. B. C. D.
4.某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
由表中数据算出线性回归方程中的b=-2,气象部门预测下个月的平均气温约为8℃,据此估计该商场下个月毛衣销售量约为( )件.
A.40 B.42 C.46. D.48
5.康托(Cantor)是十九世纪末二十世纪初德国伟大的数学家,他创立的集合论奠定了现代数学的基础.著名的“康托三分集”是数学理性思维的产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段,当记为第一次操作;再将剩下的两个区间分别均分为三段,并各自去掉中间的区间段,记为第二次操作:…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使“康托三分集”的各区间长度之和小于,则需要操作的次数n的最小值为( )(参考数据:)
A.6 B.8 C.10 D.12
6.已知,设曲线在x=k(k>0)处的切线斜率为f(k),则( )
A.f(c)<f(b)<f(a) B.f(a)<f(c)<f(b)
C.f(c)<f(a)<f(b) D.f(a)<f(b)<f(c)
7.某班举行航空知识闯关活动,共设置A,B,C三个问题.答题者可自行决定答三道题的顺序.甲有60%的可能答对问题A,80%的可能答对问题B,50%的可能答对问题C.记答题者连续答对两题的概率为p,要使得p最大,他应该先回答( )
A.问题A B.问题B C.问题C D.问题A,B和C都可以
8.若过点P(t,0)可以作曲线y=(1-x)ex的两条切线,切点分别为,则的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分有选错的得0分。
9.已知5个成对数据(x,y)的散点图如下,且y与x线性相关,若去掉点D(4,3),则下列说法正确的是( )
A.变量x与变量y呈负相关.
B.变量x与变量y的线性相关关系变强
C.残差平方和变小
D.样本相关系数r变大
10.已知递减的等差数列的前n项和为,则( )
A. B. C. D.最大
11.已知函数,则( )
A.f(x)有一个零点 B.f(x)在上单调递减
C.f(x)有一个极值点 D.若,则
12.一种疾病需要通过核酸检测来确定是否患病,检测结果呈阴性即没患病,呈阳性即为患病,已知7人中有1人患有这种疾病,先任取4人,将他们的核酸采样混在一起检测.若结果呈阳性,则表明患病者为这4人中的1人,然后再逐个检测,直到能确定患病者为止;若结果呈阴性,则在另外3人中逐个检测,直到能确定患病者为止,则( )
A.最多需要检测4次可确定患病者 B.第2次检测后就可确定患病者的概率为
C.第3次检测后就可确定患病者的概率为 D.检测次数的期望为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知函数,则______.
14.某城市每年6月份的平均气温t近似服从,若,则可估计该城市6月份平均气温低于24摄氏度的天数为______.
15.设口袋中有白球3个,黑球若干个,从中任取2个球,设抽到的球中白球个数为x个,且,则口袋中共有黑球______个.
16.已知函数,则______;设数列满足,则此数列的前2023项的和为______.
四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知数列满足.
(1)证明:是等比数列;
(2)证明:存在两个等比数列,使得成立.
18.(本题满分12分)
已知函数.
(1)若x=1是函数f(x)的极小值点,求a的值;
(2)讨论f(x)的单调性.
19.(本题满分12分)
青少年时期是视觉发育的敏感期与关键期,这个阶段的视觉发育容易受环境因素影响,某校为研究学生每天使用手机时长与近视率的关系,从全校学生中随机抽取600名学生进行不记名问卷调查,得到如下数据:有20%的学生每天使用手机超过1h,这些人的近视率为50%;每天使用手机不超过1h的学生的近视率为37.5%.
(1)若从该校学生中随机抽取一人,请根据以上数据估计该同学近视的概率;
(2)请完成2×2列联表.并根据调查数据回答:在犯错误的概率不超过5%的前提下.可以认为该校学生每天使用手机时长与近视有关吗?
视力 每天使用手机时长 合计
超过1h 不超过1h
近视
不近视
合计 600
附:.
下表是独立性检验中几个常用的小概率值和相应的临界值:
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
20.(本题满分12分)
已知等比数列的公比q>0,且满足,数列的前n项和.
(1)求数列和的通项公式;
(2)设,求数列的前2n项和.
21.(本题满分12分)
某商场为庆祝六一儿童节,举办了一场赢取小熊挂件的“定点投篮”活动,方案如下:
方案一:共投9次,每次投中得1分,否则得0分,累计所得分数记为Y;
方案二:共进行三轮投篮,每轮最多投三次,直到投中两球为止得3分,否则得0分,三轮累计所得分数记为X.
累计所得分数越多,所获得奖品越多.现在甲准备参加这个“定点投篮”活动,已知甲每次投篮的命中率为p(0<p<1),每次投篮互不影响.
(1)若,甲选择方案二,求第一轮投篮结束时,甲得3分的概率;
(2)以最终累计得分的期望值为决策依据,甲在方案一,方案二之中选其一,应选择哪个方案?
22.(本题满分12分)
已知函数.
(1)若a=2,求方程f(x)=0的解集;
(2)若f(x)有两个零点且有两个极值点,记两个极值点为,
①求a的取值范围;
②证明:.
2022~2023学年度第二学期期末考试
高二数学(参考答案及评分标准)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有-项是符合题目要求的。
BADB BACD
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.ABC. 10.ACD. 11.BCD. 12.AB.
三、填空题:本题共4小题,每小题5分,共20分.
13.6. 14.9. 15.4 16.;.(第一空2分,第二空3分)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
证明:(1)因为,所以,
又,数列是首项为3,公比为3的等比数列.
(2)存在两个等比数列,使得成立.
理由如下:由(1)知,.
所以,
因为,所以数列是首项为-2,公比为2的等比数列,
所以.所以.
令,则,
所以,存在两个等比数列,使得成立.
18.(本题满分12分)
解:(1)
令,得:,
由于x=1是函数f(x)的极小值点,所以,即a=1,
此时因为x∈(-∞,0)时,,f(x)在(-∞,0)上单调递增,
x∈(0,1)时,,f(x)在(0,1)上单调递减,
x∈(1,+∞)时,,f(x)在(1,+∞)上单调递增,
所以x=1是函数f(x)的极小值点,故a=1满足题意.
(2)时x=0或x=a,
a<0时,的解为x<a或x>0,此时f(x)在(-∞,a]和[0,+∞)上单调递增;
的解为a<x<0,此时f(x)在[a,0]上单调递减;
a>0时,的解为x<0或x>a,此时f(x)在(-∞,0]和[(a,+∞)上单调递增;
的解为0<x<a,此时f(x)在[0,a]上单调递减;
a=0时,恒成立,此时f(x)在R上单调递增.
19.(本题满分12分)
解:(1)设事件A为“任选1名学生每天使用手机超过1h”,事件B为“任选1名学生近视”,则,
由全概率公式得,
所以从该校学生中随机抽取一名学生其近视的概率为0.4.
(2)2×2列联表为
视力 每天使用手机时长 合计
超过1h 不超过1h
近视 60 180 240
不近视 60 300 360
合计 120 480 600
根据列联表中的数据,经计算得到,
所以在犯错误的概率不超过5%的前提下.可以认为该校学生每天使用手机时长与近视有关联.
20.(本题满分12分)
解:(1)依题意,由,可得
,解得,
所以,
因为数列的前n项和,所以当n=1时,,
当n≥2时,,
也满足上式,所以.
(2)由题意及(1),可知
当n为奇数时,,
当n为偶数时,,
令,则
,
,
所以,
两式相减,可得:
,
,
,
所以,
所以
.
21.(本题满分12分)
解:(1)设事件A为“甲3次投篮,前两球投进”;事件B为“甲3次投篮,最后一次才投进第2球”,则甲得3分为这两个事件的和事件,
所以,
所以第一轮投篮结束时,甲得3分的概率;
(2)选方案一,则,选方案一得分的数学期望为E(Y)=9p,
选方案二,每一轮得分只有0和3,能得3分的概率为
,
进行三轮投篮,得3分的次数ξ为随机变量,则,
进行三轮总得分X=3ξ,则选择方案二得分的期望为
,
所以,
当,两种方案期望相同,所以选方案一,二都可以,
当,方案二期望大,所以甲应该选方案二,
当,方案一期望大,所以甲应该选方案一.
22.(本题满分12分)
(1)解:若a=2,则,定义域为(0,+∞),
由f(x)=0,可得x-1-lnx=0,
设g(x)=x-1-lnx,则,
由,可得0<x<1,g(x)在(0,1)上单调递减,
由,可得x>1,g(x)在(1,+∞)上单调递增,
所以,
故方程f(x)=0的解集为.
(2)①解:令f(x)=0,得,设,
由,可得0<x<1,故h(x)在(0,1)单调递增;
由,可得x>1,故h(x)在(1,+∞)单调递减,所以,
又当x∈(0,1)时,,当时,h(x)∈(0,1),
若f(x)有两个零点,则,故a∈(0,2),
,令,得,
设,则,由,可得,
由,可得,故H(x)在上单调递增;
由,可得,故H(x)在上单调递减,,
当时,,当时,,
若f(x)有两个极值点,则a∈(0,e),
综上,a∈(0,2),
②证明:不妨令,因为且H(1)=2,得,
由为的两根得,
两式分别乘并整理得:
,
所以,
要证:,即证:,
即证:,
由于,所以,
所以只需证,
令,
,所以在上单调递减,
所以,故,
所以.
同课章节目录
