七年级数学下册试题 1.4 整式的乘法 -北师大版(含答案)
文档属性
| 名称 | 七年级数学下册试题 1.4 整式的乘法 -北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 693.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览




文档简介
1.4 整式的乘法
第一课时
一、选择题
1.下列运算正确的是( )
A. B.
C. D.
2.若,则( )
A. B. C. D.2
3.若,则m,n的值分别为( )
A., B., C., D.,
4.将多项式化简后不含项,则的值是( )
A. B. C. D.
5.小羽制作了如图所示的卡片类,类,类各张,其中,两类卡片都是正方形,类卡片是长方形,现要拼一个长为,宽为的大长方形,那么所准备的类卡片的张数( )
A.够用,剩余4张 B.够用,剩余5张
C.不够用,还缺4张 D.不够用,还缺5张
6.我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在(n为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按a的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则展开式中含项的系数是( )
, ……
A.2016 B.2017 C.2018 D.2019
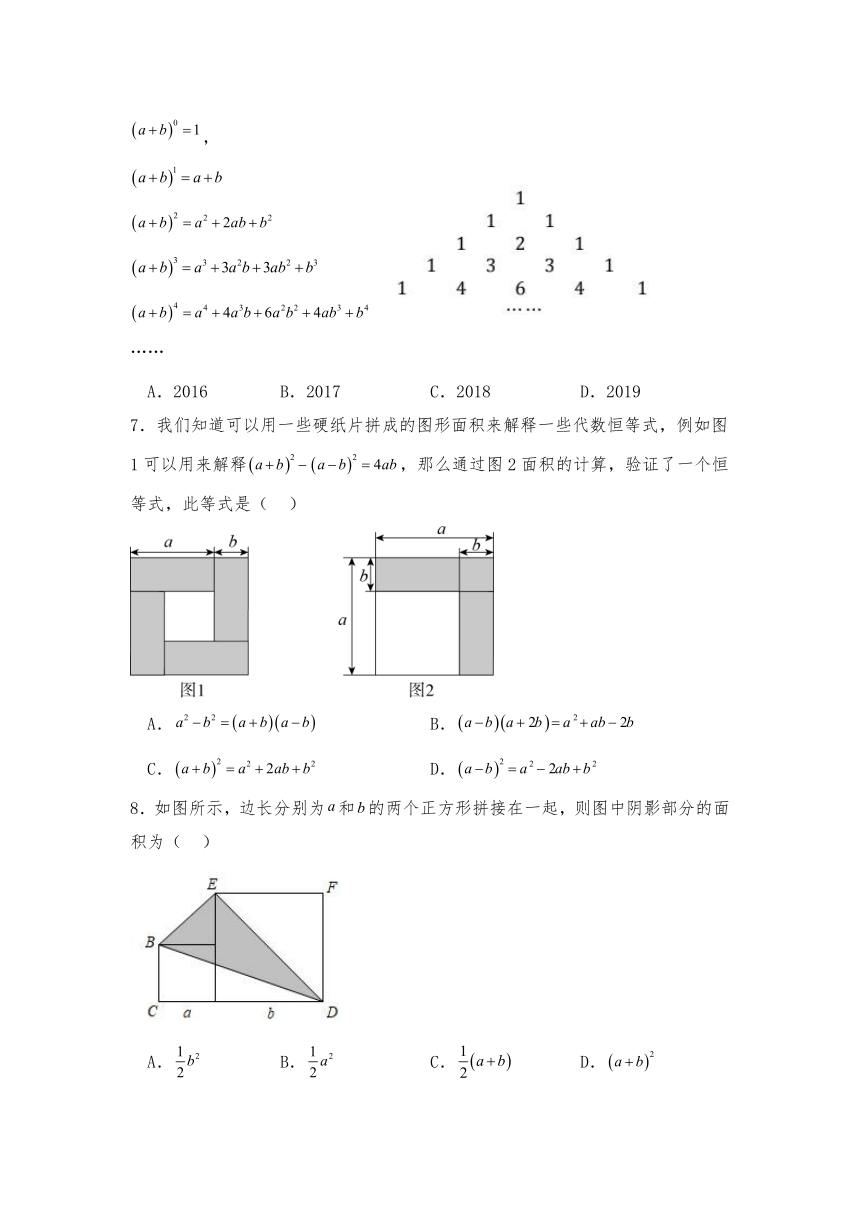
7.我们知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式,例如图1可以用来解释,那么通过图2面积的计算,验证了一个恒等式,此等式是( )
A. B.
C. D.
8.如图所示,边长分别为和的两个正方形拼接在一起,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
9.计算:___________.
10.如果,那么的值为______.
11.已知的结果中不含项,则m=__________.
12.如果的结果中不含有一次项,那么常数m的值为____________.
13.已知,则_____, _____.
14.若,则的结果为___________.
15.如果长方形的长为,宽为,那么长方形的面积为______.
16.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为,宽为的大长方形,则需要___________张C类卡片.
三、解答题
17.计算:
(1); (2); (3).
18.若的积中不含的一次项与的二次项.
(1)求的值;
(2)求式子的值.
19.小红准备完成题目:计算,她发现第一个因式的一次项系数被墨水遮挡住了.
(1)她把被遮住的一次项系数猜成3,请你完成计算:;
(2)老师说:“你猜错了,这个题目的正确答案是不含一次项的,”请通过计算说明原题中被遮住的一次项系数是多少?
20.如图,把8张长为a,宽为b的小长方形纸片摆放在一个大长方形纸盒内,空白部分分别用A,B表示,两个摆放小纸片的长方形(阴影)公共的部分边长为m,(用a,b,m分别表示周长和面积)
(1)填空:①空白部分A的周长__________,面积_____________,
②空白部分B的周长______________,面积________________;
(2)若,求,的代数式.
第二课时
一、选择题
1.如果A、B都是关于x的单项式,且是一个八次单项式,是一个六次多项式,那么的次数( )
A.一定是八次 B.一定是六次
C.一定是四次 D.无法确定
2.利用图形的分、和、移、补,探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若,,则矩形的面积是 ( )
A. B. C. D.
3.若,则( )
A., B., C., D.,
4. 若的展开式中不含,则的值( )
A. B. C. D.
5.若一个只含字母的多项式的项数是偶数,用该多项式去乘,若该多项式的项数是奇数,则用该多项式去乘,称这为第一次操作;若第一次操作后所得多项式的项数是偶数,用该多项式去乘,若该多项式的项数是奇数,则用该多项式去乘称这为第二此操作,以此类推.
①将多项式以上述方式进行2次操作后所得多项式项数是5;
②将多项式以上述方式进行3次操作后,多项式的所有系数和为0;
③将多项式以上述方式进行4次操作后,当时,所得多项式的值为243;
④将多项式以上述方式进行次操作后所得多项式为;
四个结论错误的有( )
A.0 B.1 C.2 D.3
6.小轩计算一道整式乘法的题:,由于小轩将第一个多项式中的“+2m”抄成“-2m”,得到的结果为.则m的值为( )
A.4 B.5 C.6 D.7
7.若,,为正整数,则的最大值与最小值的差为( )
A.25 B.24 C.74 D.8
二、填空题
8.计算:___________.
9.如图,一个长方形的长为a,宽为b,将它剪去一个正方形①,然后从剩余的长方形中再剪去一个正方形③,最后剩下长方形②,则长方形②的面积为__________.
10.在的运算结果中,项的系数与常数项相等,则的值是______.
11.如图是中国宋代的“贾宪三角”,又称“杨辉三角”,分别展示了二项式乘方展开式的字母及字母规律和系数规律.观察下列各式及其展开式,展开式的第三项为______.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
12.已知的展开式中不含三次项和四次项,则展开式中二次项和一次项的系数之和为______.
13.如图,在正方形内,将2张①号长方形纸片和3张②号长方形纸片按图1和图2两种方式放置(放置的纸片间没有重叠部分),正方形中未被覆盖的部分(阴影部分)的周长相等.
(1)若①号长方形纸片的宽为2厘米,则②号长方形纸片的宽为_______厘米;
(2)若①号长方形纸片的面积为40平方厘米,则②号长方形纸片的面积是_________平方厘米.
14.已知长方形可以按图所示方式分成九部分,在变化的过程中,下面说法正确的有______(请将所有正确的编号填在横线上)
①图中存在三部分的周长之和恰好等于长方形的周长
②长方形的长宽之比可能为
③当长方形为正方形时,九部分都为正方形
④当长方形的周长为时,它的面积可能为
15.有若干张如图所示的正方形和长方形卡片,如果要拼一个长为,宽为的矩形,则需要A类卡片______张,B类卡片______张,C类卡片______张,请你在右下角的大矩形中画出一种拼法.(标上卡片名称)
三、解答题
16.已知的展开式中不含x的二次项,常数项是,求m,n的值.
17.若的展开式中不含,项(其中m,n均为常数).
(1)求m,n的值;
(2)先化简,然后在(1)的条件下,求A的值.
18.如图,现有一块长为米,宽为米的长方形地块,规划将阴影部分进行绿化,中间预留部分是边长为a米的正方形.
(1)求绿化的面积S(用含a,b的代数式表示,并化简);
(2)若,绿化成本为20元/平方米,则完成绿化共需要多少元?
19.“数形结合百般好”.在代数式的学习过程中我们可以结合图形理解相关公式的产生,如图1所示的正方形,我们可以利用两种不同的方法计算它的面积,从而得到完全平方公式:.
请结合以上知识,解答下列问题:
(1)写出图2所示的长方形所表示的数学等式 ;
(2)根据图3得到的结论,解决下列问题:
若,,求代数式的值;
(3)小明同学用图4中x张边长为a的正方形纸片,y张边长为b的正方形纸片,z张边长分别为a,b的长方形纸片拼出一个面积为的长方形,求代数式的值.
第一课时答案
一、选择题
C.A.B.A.C.D.D.A.
二、填空题
9..
10..
11.6
12..
13.,.
14.21.
15..
16..
三、解答题
17.(1)解:
.
(2)
;
(3)
.
18.(1)解:
∵不含x的一次项与x的二次项,
∴,
∴,.
(2)当,时,
原式
.
19.(1)解:
;
(2)解:设第一次因式的一次项系数为a,则原题目变为,
,
∵的计算结果不含一次项,
∴,
∴,
∴被遮住的一次项系数是2.
20.(1)解:根据题意得:空白部分A的边长分别为a,,
∴①空白部分A的周长,面积;
故答案为:,;
②根据题意得:空白部分B的边长分别为,
∴空白部分B的周长,面积,
故答案为:,;
(2)解:
;
当时,
;
第二课时答案
一、选择题
B.C.C.D.C.C.A.
二、填空题
8..
9..
10..
11..
12.
13..
14.①③.
15.2;1;3.
三、解答题
16.解:
,
∵展开式中不含x的二次项,常数项是,
∴且,
解得:.
17.(1)原式
,
由題意可知:,,
∴,,
(2)原式
,
当,时,
原式
.
18.(1)解:
平方米;
(2)解:当时,
平方米,
元.
答:完成绿化共需要3340元.
19.(1)拼成的大长方形面积之和,
各个小图形面积之和,
∴图2所表示的数学等式是.
故答案为:.
(2)图(3)中大正方形的面积=,
各个小图形面积之和=,
∴.
∵,.
∴,
即,
∴.
(3)大长方形的面积为:,
∵小图形的面积分别为,
∴.
∴.
第一课时
一、选择题
1.下列运算正确的是( )
A. B.
C. D.
2.若,则( )
A. B. C. D.2
3.若,则m,n的值分别为( )
A., B., C., D.,
4.将多项式化简后不含项,则的值是( )
A. B. C. D.
5.小羽制作了如图所示的卡片类,类,类各张,其中,两类卡片都是正方形,类卡片是长方形,现要拼一个长为,宽为的大长方形,那么所准备的类卡片的张数( )
A.够用,剩余4张 B.够用,剩余5张
C.不够用,还缺4张 D.不够用,还缺5张
6.我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在(n为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按a的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则展开式中含项的系数是( )
, ……
A.2016 B.2017 C.2018 D.2019
7.我们知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式,例如图1可以用来解释,那么通过图2面积的计算,验证了一个恒等式,此等式是( )
A. B.
C. D.
8.如图所示,边长分别为和的两个正方形拼接在一起,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
9.计算:___________.
10.如果,那么的值为______.
11.已知的结果中不含项,则m=__________.
12.如果的结果中不含有一次项,那么常数m的值为____________.
13.已知,则_____, _____.
14.若,则的结果为___________.
15.如果长方形的长为,宽为,那么长方形的面积为______.
16.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为,宽为的大长方形,则需要___________张C类卡片.
三、解答题
17.计算:
(1); (2); (3).
18.若的积中不含的一次项与的二次项.
(1)求的值;
(2)求式子的值.
19.小红准备完成题目:计算,她发现第一个因式的一次项系数被墨水遮挡住了.
(1)她把被遮住的一次项系数猜成3,请你完成计算:;
(2)老师说:“你猜错了,这个题目的正确答案是不含一次项的,”请通过计算说明原题中被遮住的一次项系数是多少?
20.如图,把8张长为a,宽为b的小长方形纸片摆放在一个大长方形纸盒内,空白部分分别用A,B表示,两个摆放小纸片的长方形(阴影)公共的部分边长为m,(用a,b,m分别表示周长和面积)
(1)填空:①空白部分A的周长__________,面积_____________,
②空白部分B的周长______________,面积________________;
(2)若,求,的代数式.
第二课时
一、选择题
1.如果A、B都是关于x的单项式,且是一个八次单项式,是一个六次多项式,那么的次数( )
A.一定是八次 B.一定是六次
C.一定是四次 D.无法确定
2.利用图形的分、和、移、补,探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若,,则矩形的面积是 ( )
A. B. C. D.
3.若,则( )
A., B., C., D.,
4. 若的展开式中不含,则的值( )
A. B. C. D.
5.若一个只含字母的多项式的项数是偶数,用该多项式去乘,若该多项式的项数是奇数,则用该多项式去乘,称这为第一次操作;若第一次操作后所得多项式的项数是偶数,用该多项式去乘,若该多项式的项数是奇数,则用该多项式去乘称这为第二此操作,以此类推.
①将多项式以上述方式进行2次操作后所得多项式项数是5;
②将多项式以上述方式进行3次操作后,多项式的所有系数和为0;
③将多项式以上述方式进行4次操作后,当时,所得多项式的值为243;
④将多项式以上述方式进行次操作后所得多项式为;
四个结论错误的有( )
A.0 B.1 C.2 D.3
6.小轩计算一道整式乘法的题:,由于小轩将第一个多项式中的“+2m”抄成“-2m”,得到的结果为.则m的值为( )
A.4 B.5 C.6 D.7
7.若,,为正整数,则的最大值与最小值的差为( )
A.25 B.24 C.74 D.8
二、填空题
8.计算:___________.
9.如图,一个长方形的长为a,宽为b,将它剪去一个正方形①,然后从剩余的长方形中再剪去一个正方形③,最后剩下长方形②,则长方形②的面积为__________.
10.在的运算结果中,项的系数与常数项相等,则的值是______.
11.如图是中国宋代的“贾宪三角”,又称“杨辉三角”,分别展示了二项式乘方展开式的字母及字母规律和系数规律.观察下列各式及其展开式,展开式的第三项为______.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
12.已知的展开式中不含三次项和四次项,则展开式中二次项和一次项的系数之和为______.
13.如图,在正方形内,将2张①号长方形纸片和3张②号长方形纸片按图1和图2两种方式放置(放置的纸片间没有重叠部分),正方形中未被覆盖的部分(阴影部分)的周长相等.
(1)若①号长方形纸片的宽为2厘米,则②号长方形纸片的宽为_______厘米;
(2)若①号长方形纸片的面积为40平方厘米,则②号长方形纸片的面积是_________平方厘米.
14.已知长方形可以按图所示方式分成九部分,在变化的过程中,下面说法正确的有______(请将所有正确的编号填在横线上)
①图中存在三部分的周长之和恰好等于长方形的周长
②长方形的长宽之比可能为
③当长方形为正方形时,九部分都为正方形
④当长方形的周长为时,它的面积可能为
15.有若干张如图所示的正方形和长方形卡片,如果要拼一个长为,宽为的矩形,则需要A类卡片______张,B类卡片______张,C类卡片______张,请你在右下角的大矩形中画出一种拼法.(标上卡片名称)
三、解答题
16.已知的展开式中不含x的二次项,常数项是,求m,n的值.
17.若的展开式中不含,项(其中m,n均为常数).
(1)求m,n的值;
(2)先化简,然后在(1)的条件下,求A的值.
18.如图,现有一块长为米,宽为米的长方形地块,规划将阴影部分进行绿化,中间预留部分是边长为a米的正方形.
(1)求绿化的面积S(用含a,b的代数式表示,并化简);
(2)若,绿化成本为20元/平方米,则完成绿化共需要多少元?
19.“数形结合百般好”.在代数式的学习过程中我们可以结合图形理解相关公式的产生,如图1所示的正方形,我们可以利用两种不同的方法计算它的面积,从而得到完全平方公式:.
请结合以上知识,解答下列问题:
(1)写出图2所示的长方形所表示的数学等式 ;
(2)根据图3得到的结论,解决下列问题:
若,,求代数式的值;
(3)小明同学用图4中x张边长为a的正方形纸片,y张边长为b的正方形纸片,z张边长分别为a,b的长方形纸片拼出一个面积为的长方形,求代数式的值.
第一课时答案
一、选择题
C.A.B.A.C.D.D.A.
二、填空题
9..
10..
11.6
12..
13.,.
14.21.
15..
16..
三、解答题
17.(1)解:
.
(2)
;
(3)
.
18.(1)解:
∵不含x的一次项与x的二次项,
∴,
∴,.
(2)当,时,
原式
.
19.(1)解:
;
(2)解:设第一次因式的一次项系数为a,则原题目变为,
,
∵的计算结果不含一次项,
∴,
∴,
∴被遮住的一次项系数是2.
20.(1)解:根据题意得:空白部分A的边长分别为a,,
∴①空白部分A的周长,面积;
故答案为:,;
②根据题意得:空白部分B的边长分别为,
∴空白部分B的周长,面积,
故答案为:,;
(2)解:
;
当时,
;
第二课时答案
一、选择题
B.C.C.D.C.C.A.
二、填空题
8..
9..
10..
11..
12.
13..
14.①③.
15.2;1;3.
三、解答题
16.解:
,
∵展开式中不含x的二次项,常数项是,
∴且,
解得:.
17.(1)原式
,
由題意可知:,,
∴,,
(2)原式
,
当,时,
原式
.
18.(1)解:
平方米;
(2)解:当时,
平方米,
元.
答:完成绿化共需要3340元.
19.(1)拼成的大长方形面积之和,
各个小图形面积之和,
∴图2所表示的数学等式是.
故答案为:.
(2)图(3)中大正方形的面积=,
各个小图形面积之和=,
∴.
∵,.
∴,
即,
∴.
(3)大长方形的面积为:,
∵小图形的面积分别为,
∴.
∴.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
