七年级数学下册试题 1.7 整式的除法 -北师大版(含答案)
文档属性
| 名称 | 七年级数学下册试题 1.7 整式的除法 -北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览




文档简介
1.7 整式的除法
第一课时
一、选择题
1.下列计算中,正确的是( )
A. B.
C. D.
2.已知,四张形状、大小完全相同的小长方形(如图1所示),将其不重叠地放在一个长为,宽为的大长方形中(如图2所示),其中未被覆盖的部分用阴影表示,则阴影部分的周长为( )
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
4.如图,将一张长方形的铁皮剪去一个小长方形,余下的阴影部分面积是( ).
A. B. C. D.
5.在求的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:①,然后在①式的两边都乘以6,得 ②,②①得,即,所以,得出答案后爱动脑筋的小林想:如果把“6”换成字母“a”(且),能否求出的值?你的答案是( )
A. B. C. D.
6.长方形的面积为,若它的一边长为,则它的周长为( )
A. B. C. D.
7.小明在做作业的时候,不小心把墨水滴到了作业本上,■,阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的一项是( )
A. B. C. D.
8.当时,代数式的值是( ).
A.6.25 B. C. D.0.25
二、填空题
9.计算__.
10.渭南市园林局为美化城区环境,计划在一块长方形空地上种植某种草皮,已知长方形空地的面积为平方米,宽为米,则这块空地的长为______米.
11.如图,从边长为的正方形纸片中剪去一个边长为2的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的一条边长是a,另一条边长是__________.
12.湖北省科技馆位于武汉市光谷,其中“数理世界”展厅的WFI的密码被设计成如图数学问题.小东在参观时认真思索,输入密码后顺利地连接到网络,则他输入的密码是______.
13.现规定一种新运算,其中a、b为实数,则等于______.
14.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为,则宽为 _____.
15.如果用★表示一种新的运算符号,而且规定有如下的运算法则: ,则_____.
16.将展开后,结果不含x的一次项,则m的值为_______________.
三、解答题
17.计算:
(1); (2);
(3); (4);
(5); (6).
18.(1)已知:,求的值;
(2)下边是嘉琪计算的解题过程请你判断是否正确?若有错误,请写出正确的解题过程.
.
19.探究下面的问题:
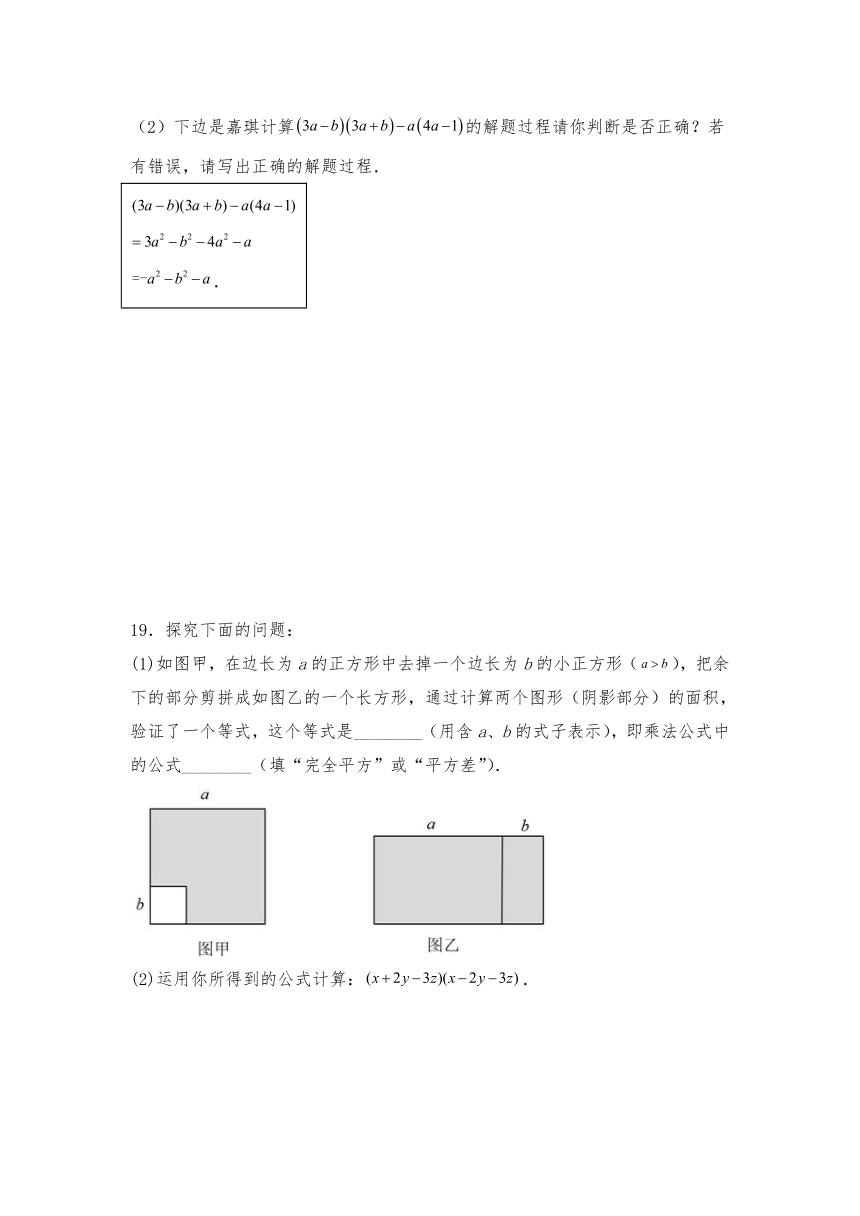
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用含a、b的式子表示),即乘法公式中的公式________(填“完全平方”或“平方差”).
(2)运用你所得到的公式计算:.
20.数学老师给学生出了一道题:当,时,求的值.题目出完后,小明说:“老师给出的条件是多余的.”小亮说:“不是多余的.”你同意谁的说法?为什么?请给出推理过程.
第二课时
一、选择题
1.计算( ),正确的结果是( )
A.16 B.42 C. D.
2.已知实数m,n满足,则的最小值为( )
A. B. C. D.
3.如果,那么代数式的值为( )
A.0 B. C.1 D.3
4.若定义 表示, 表示,则运算÷的结果为( )
A. B. C. D.
5.若,则,的值分别为( )
A.3,2 B.2,2 C.2,3 D.3,1
6.如图,正方形的边长为,点在边上,四边形也是正方形,它的边长为,连接、、.若,则的面积为( )
A. B. C. D.
7.将多项式除以后得商式,余式为0,则的值为( )
A.3 B.23 C.25 D.29
8.设x,y为任意有理数,定义运算:x*y=(x+1)(y+1)-1,
得到下列五个结论:①x*y=y*x ②x*(y+z)=x*y+x*z
③(x+1)*(x-1)=x*x-1 ④x*0=0
⑤(x+1)*(x+1)=x*x+2*x+1其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
9.下面是一道例题及其解答过程的一部分,其中A是关于m的多项式,请写出多项式A,并将该例题的解答过程补充完整.
例:先去括号,再合并同类项:. 解: =_____,多项式A为____.
10.若,那么的值为 __.
11.①
②
③
……
题:猜想__________.
题:当,代数式___________.
12.已知,则代数式的值为 _____.
13.数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“(3x﹣■+1)=”那么“■”中的一项是 _____.
14.小玲想借助学过的几何图形设计图案,首先她将如图1的小长方形和如图2的小正方形组合成如图3的大正方形图案,已知小长方形的长为,宽为,则图2的小正方形的边长可用关于和的代数式表示为______;小玲随后用3个如图3的完全相同的图案和8个如图1的小长方形,组合成如图4的大长方形图案,则图4中阴影部分面积与整个图形的面积之比为______.
15.在综合拓展实验课中,某小组裁剪出了1张边长为a的正方形纸片,3张长为a,宽为b的长方形纸片和1张边长为b的正方形纸片如图1.将这些纸片无缝拼接放置在长方形ABCD中如图2所示,若图2中的阴影部分的周长:长方形ABCD的周长,则图2中阴影部分的面积:长方形ABCD的面积=________.
16.现有一张边长为的大正方形卡片和三张边长为的小正方形卡片,如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3,则图3中阴影部分的面积为______(用含有,的代数式表示):已知图3中的阴影部分的面积比图2中的阴影部分的面积大,则小正方形卡片的面积是_______.
三、解答题
17.计算:
(1);
(2).
18.正方形中,点G是边上一点(不与点C,D重合),以为边在正方形外作正方形,且B,C,E三点在同一条直线上,设正方形和正方形的边长分别为a和b().
(1)求图1中阴影部分的面积(用含a,b的代数式表示);
(2)当时,求图1中阴影部分的面积的值;
(3)当时,请直接写出图2中阴影部分的面积的值.
19.对于任何实数,我们规定符号,例如:.
(1)按照这个规定请你计算的值;
(2)按规定请写出的结果;
(3)当a取的相反数时,请计算的值.
20.某校准备在网上订购一批某品牌足球和跳绳,在查阅某网购平台后发现足球每个定价元,跳绳每根定价元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一根跳绳:B网店:足球和跳绳都按定价的90%付款.
已知该校要购买足球个,跳绳x根().
(1)在A网店购买足球和跳绳所需费用为____________元,在B网店购买足球和跳绳所需费用为____________元;(用含x的代数式表示)
(2)当时,且只选择其中一家网店购买,通过计算说明此时在哪家网店购买较为合算?
第一课时答案
一、选择题
C.D.B.D.A.B.A.D.
二、填空题
9..
10..
11..
12.
13.(.
14..
15..
16.
三、解答题
17.(1)解:原式;
(2)解:原式;
(3)原式;
(4)原式;
(5)原式;
(6)原式.
18.解:(1),
(2)不正确,解题过程如下:
.
19.(1)解:根据题意得:图甲阴影部分面积等于 ,图乙阴影部分面积等于,
∴这个等式是 ,即乘法公式中的平方差公式.
故答案为,平方差.
(2)解:
.
20.解:同意小亮的说法,理由如下,
;
结果与无关,条件是多余的
当时,原式,
∴小亮的说法正确.
第二课时答案
一、选择题
D.A.C.A.C.B.D.B.
二、填空题
9.
10.1.
11.或.
12.5
13.2y.
14.a b;.
15..
16.(a﹣b)2;5.
三、解答题
17.(1)解:原式
;
(2)原式
.
18.(1)
;
(2)∵,
∴
;
(3)如图,延长和,交于点H.
∴
.
∵,
∴.
19.(1)解:;
(2)解:
;
(3)解:的相反数是2,
当时,
.
20.(1)解:A店购买需付款:(元);
B店购买需付款:(元),
故答案为:;;
(2)解:当时,
在A网店购买需付款:(元),
在B网店购买需付款: (元),
,
∴当时,应选择在A网店购买合算.
第一课时
一、选择题
1.下列计算中,正确的是( )
A. B.
C. D.
2.已知,四张形状、大小完全相同的小长方形(如图1所示),将其不重叠地放在一个长为,宽为的大长方形中(如图2所示),其中未被覆盖的部分用阴影表示,则阴影部分的周长为( )
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
4.如图,将一张长方形的铁皮剪去一个小长方形,余下的阴影部分面积是( ).
A. B. C. D.
5.在求的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:①,然后在①式的两边都乘以6,得 ②,②①得,即,所以,得出答案后爱动脑筋的小林想:如果把“6”换成字母“a”(且),能否求出的值?你的答案是( )
A. B. C. D.
6.长方形的面积为,若它的一边长为,则它的周长为( )
A. B. C. D.
7.小明在做作业的时候,不小心把墨水滴到了作业本上,■,阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的一项是( )
A. B. C. D.
8.当时,代数式的值是( ).
A.6.25 B. C. D.0.25
二、填空题
9.计算__.
10.渭南市园林局为美化城区环境,计划在一块长方形空地上种植某种草皮,已知长方形空地的面积为平方米,宽为米,则这块空地的长为______米.
11.如图,从边长为的正方形纸片中剪去一个边长为2的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的一条边长是a,另一条边长是__________.
12.湖北省科技馆位于武汉市光谷,其中“数理世界”展厅的WFI的密码被设计成如图数学问题.小东在参观时认真思索,输入密码后顺利地连接到网络,则他输入的密码是______.
13.现规定一种新运算,其中a、b为实数,则等于______.
14.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为,则宽为 _____.
15.如果用★表示一种新的运算符号,而且规定有如下的运算法则: ,则_____.
16.将展开后,结果不含x的一次项,则m的值为_______________.
三、解答题
17.计算:
(1); (2);
(3); (4);
(5); (6).
18.(1)已知:,求的值;
(2)下边是嘉琪计算的解题过程请你判断是否正确?若有错误,请写出正确的解题过程.
.
19.探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用含a、b的式子表示),即乘法公式中的公式________(填“完全平方”或“平方差”).
(2)运用你所得到的公式计算:.
20.数学老师给学生出了一道题:当,时,求的值.题目出完后,小明说:“老师给出的条件是多余的.”小亮说:“不是多余的.”你同意谁的说法?为什么?请给出推理过程.
第二课时
一、选择题
1.计算( ),正确的结果是( )
A.16 B.42 C. D.
2.已知实数m,n满足,则的最小值为( )
A. B. C. D.
3.如果,那么代数式的值为( )
A.0 B. C.1 D.3
4.若定义 表示, 表示,则运算÷的结果为( )
A. B. C. D.
5.若,则,的值分别为( )
A.3,2 B.2,2 C.2,3 D.3,1
6.如图,正方形的边长为,点在边上,四边形也是正方形,它的边长为,连接、、.若,则的面积为( )
A. B. C. D.
7.将多项式除以后得商式,余式为0,则的值为( )
A.3 B.23 C.25 D.29
8.设x,y为任意有理数,定义运算:x*y=(x+1)(y+1)-1,
得到下列五个结论:①x*y=y*x ②x*(y+z)=x*y+x*z
③(x+1)*(x-1)=x*x-1 ④x*0=0
⑤(x+1)*(x+1)=x*x+2*x+1其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
9.下面是一道例题及其解答过程的一部分,其中A是关于m的多项式,请写出多项式A,并将该例题的解答过程补充完整.
例:先去括号,再合并同类项:. 解: =_____,多项式A为____.
10.若,那么的值为 __.
11.①
②
③
……
题:猜想__________.
题:当,代数式___________.
12.已知,则代数式的值为 _____.
13.数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“(3x﹣■+1)=”那么“■”中的一项是 _____.
14.小玲想借助学过的几何图形设计图案,首先她将如图1的小长方形和如图2的小正方形组合成如图3的大正方形图案,已知小长方形的长为,宽为,则图2的小正方形的边长可用关于和的代数式表示为______;小玲随后用3个如图3的完全相同的图案和8个如图1的小长方形,组合成如图4的大长方形图案,则图4中阴影部分面积与整个图形的面积之比为______.
15.在综合拓展实验课中,某小组裁剪出了1张边长为a的正方形纸片,3张长为a,宽为b的长方形纸片和1张边长为b的正方形纸片如图1.将这些纸片无缝拼接放置在长方形ABCD中如图2所示,若图2中的阴影部分的周长:长方形ABCD的周长,则图2中阴影部分的面积:长方形ABCD的面积=________.
16.现有一张边长为的大正方形卡片和三张边长为的小正方形卡片,如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3,则图3中阴影部分的面积为______(用含有,的代数式表示):已知图3中的阴影部分的面积比图2中的阴影部分的面积大,则小正方形卡片的面积是_______.
三、解答题
17.计算:
(1);
(2).
18.正方形中,点G是边上一点(不与点C,D重合),以为边在正方形外作正方形,且B,C,E三点在同一条直线上,设正方形和正方形的边长分别为a和b().
(1)求图1中阴影部分的面积(用含a,b的代数式表示);
(2)当时,求图1中阴影部分的面积的值;
(3)当时,请直接写出图2中阴影部分的面积的值.
19.对于任何实数,我们规定符号,例如:.
(1)按照这个规定请你计算的值;
(2)按规定请写出的结果;
(3)当a取的相反数时,请计算的值.
20.某校准备在网上订购一批某品牌足球和跳绳,在查阅某网购平台后发现足球每个定价元,跳绳每根定价元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一根跳绳:B网店:足球和跳绳都按定价的90%付款.
已知该校要购买足球个,跳绳x根().
(1)在A网店购买足球和跳绳所需费用为____________元,在B网店购买足球和跳绳所需费用为____________元;(用含x的代数式表示)
(2)当时,且只选择其中一家网店购买,通过计算说明此时在哪家网店购买较为合算?
第一课时答案
一、选择题
C.D.B.D.A.B.A.D.
二、填空题
9..
10..
11..
12.
13.(.
14..
15..
16.
三、解答题
17.(1)解:原式;
(2)解:原式;
(3)原式;
(4)原式;
(5)原式;
(6)原式.
18.解:(1),
(2)不正确,解题过程如下:
.
19.(1)解:根据题意得:图甲阴影部分面积等于 ,图乙阴影部分面积等于,
∴这个等式是 ,即乘法公式中的平方差公式.
故答案为,平方差.
(2)解:
.
20.解:同意小亮的说法,理由如下,
;
结果与无关,条件是多余的
当时,原式,
∴小亮的说法正确.
第二课时答案
一、选择题
D.A.C.A.C.B.D.B.
二、填空题
9.
10.1.
11.或.
12.5
13.2y.
14.a b;.
15..
16.(a﹣b)2;5.
三、解答题
17.(1)解:原式
;
(2)原式
.
18.(1)
;
(2)∵,
∴
;
(3)如图,延长和,交于点H.
∴
.
∵,
∴.
19.(1)解:;
(2)解:
;
(3)解:的相反数是2,
当时,
.
20.(1)解:A店购买需付款:(元);
B店购买需付款:(元),
故答案为:;;
(2)解:当时,
在A网店购买需付款:(元),
在B网店购买需付款: (元),
,
∴当时,应选择在A网店购买合算.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
