八年级数学下册试题 1.1 等腰三角形同步练习-北师大版(含答案)
文档属性
| 名称 | 八年级数学下册试题 1.1 等腰三角形同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 474.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 17:39:19 | ||
图片预览


文档简介
1.1 等腰三角形
一、单选题
1.△ABC中,AB=AC,D为BC边的中点,以下结论:(1)AD⊥BC; (2)∠B=∠C;(3)AD平分∠BAC,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.若等腰三角形的两边长为3和7,则该等腰三角形的周长为( )
A.10 B.13 C.17 D.13或17
3.等腰三角形的底角等于,则该等腰三角形的顶角度数为( )
A. B. C.或 D.或
4.如图,在中,为BC边上的中线,,则的度数为( )
A. B. C. D.
5.如图,△是等边三角形,是边上的高,且,是的中点,是上的一个动点,则与的和最小是( )
A.3 B.4 C.6 D.8
6.如图,中,,,,,则的度数为( )
A. B. C. D.
7.下列结论中:①有一个外角是的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的等腰三角形是等边三角形;④三个内角都相等的三角形是等边三角形.其中正确的个数是( )
A. B. C. D.
8.如图,在△中,,为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点为圆心,长为半径作圆弧,交于点;③以点为圆心,长为半径作圆弧,交②中所作的圆弧于点;④作射线交于点.下列说法不正确的是( )
A.= B.=∠ACB
C.∠CHB=∠A+∠B D.=∠HCB
9.如图所示,在中,,是边上任意一点,过作于,于,若,,则AB=( )
A.5 B.6 C.7 D.8
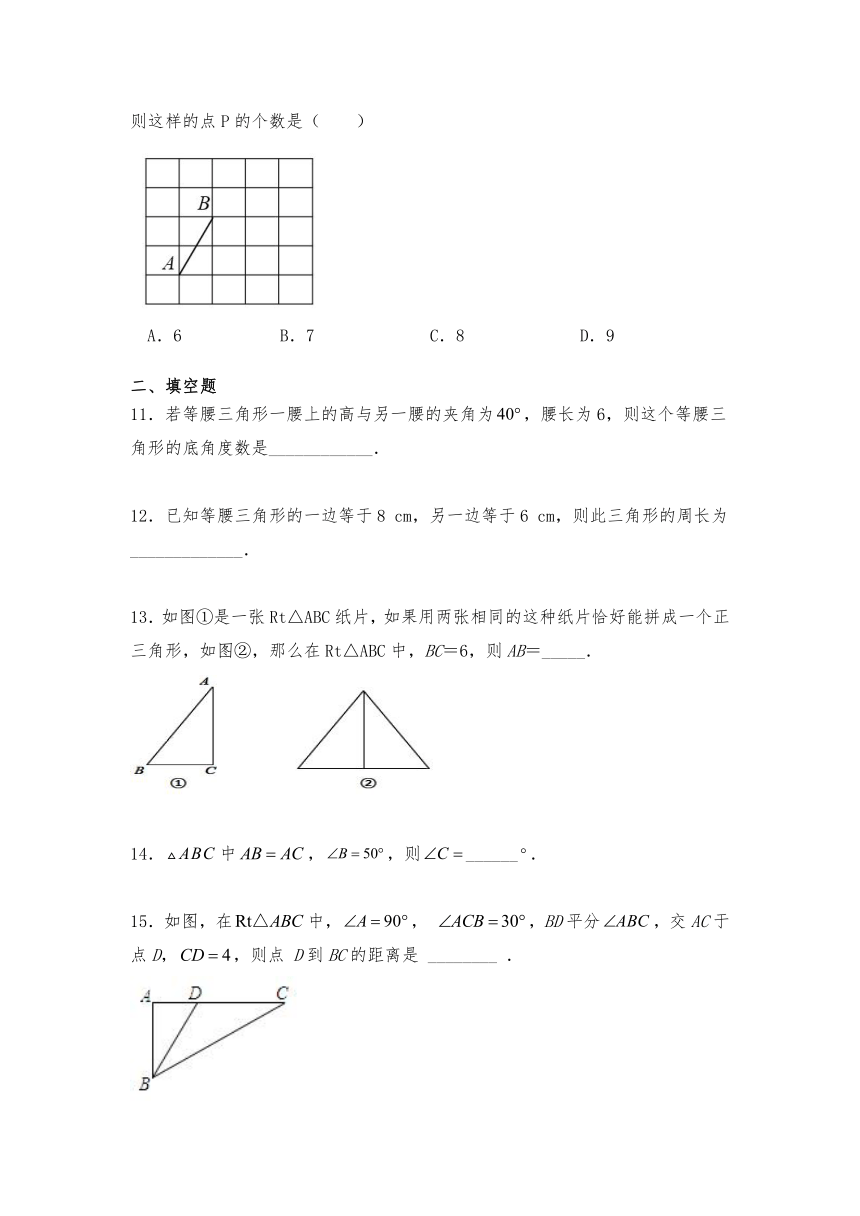
10.在网格中作出点P,使△ABP以AB为腰的等腰三角形,且点P要在格点上,则这样的点P的个数是( )
A.6 B.7 C.8 D.9
二、填空题
11.若等腰三角形一腰上的高与另一腰的夹角为,腰长为6,则这个等腰三角形的底角度数是____________.
12.已知等腰三角形的一边等于8 cm,另一边等于6 cm,则此三角形的周长为 _____________.
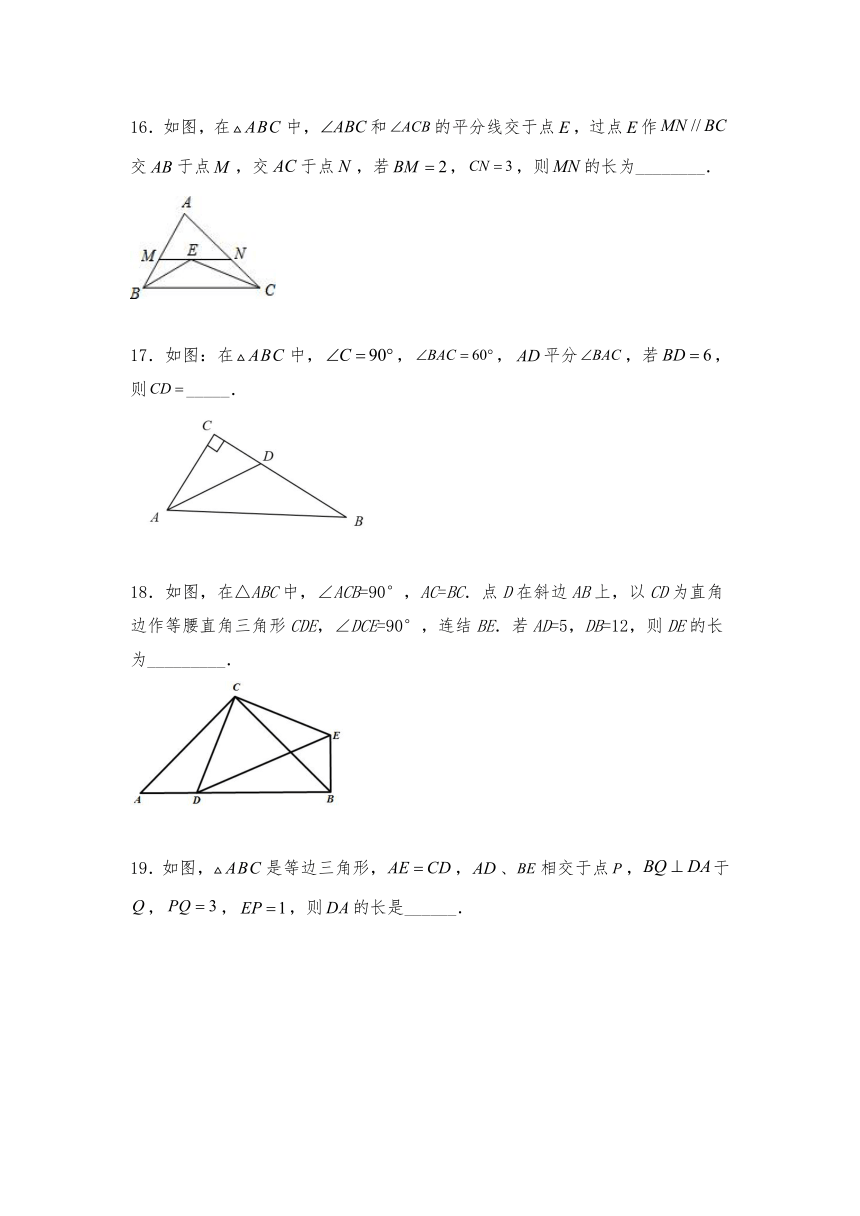
13.如图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图②,那么在Rt△ABC中,BC=6,则AB=_____.
14.中,,则______.
15.如图,在中,, ,BD平分,交AC于点D,,则点 D到BC的距离是 ________ .
16.如图,在中,和的平分线交于点,过点作交于点,交于点,若,,则的长为________.
17.如图:在中,,,平分,若,则_____.
18.如图,在△ABC中,∠ACB=90°,AC=BC.点D在斜边AB上,以CD为直角边作等腰直角三角形CDE,∠DCE=90°,连结BE.若AD=5,DB=12,则DE的长为_________.
19.如图,是等边三角形,,、相交于点,于,,,则的长是______.
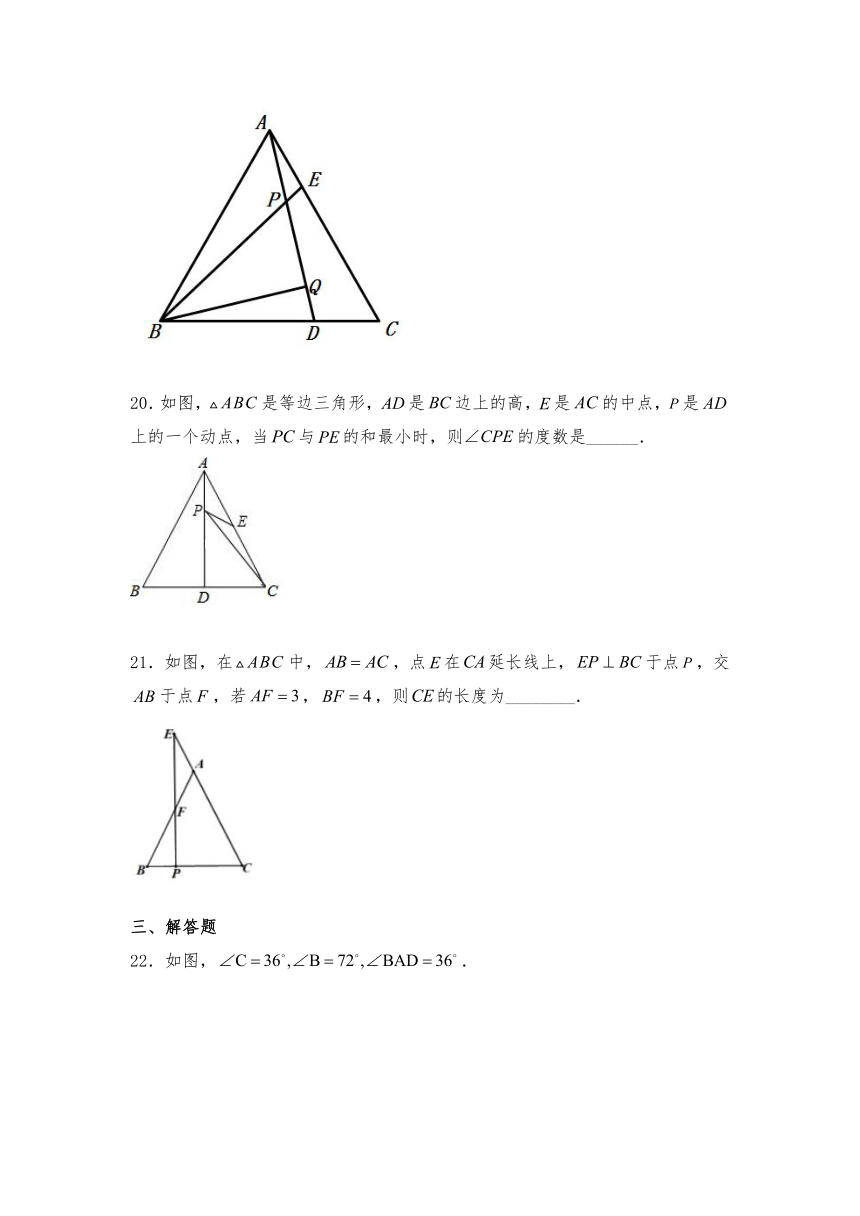
20.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,则的度数是______.
21.如图,在中,,点在延长线上,于点,交于点,若,,则的长度为________.
三、解答题
22.如图,.
(1)写出图中所有的等腰三角形;
(2)选其中一个等腰三角形加以证明.
23.如图,在中,点是上一点,,,求的度数.
24.如图1,在边长为6的等边△ABC中,点D从点A开始在射线AB上运动,速度为1个单位/秒,点F同时从C出发,以相同的速度沿射线BC方向运动,过点D作DE⊥AC,连接DF交射线AC于点G,设点D的运动时间为t秒;
(1)当DF⊥AB时,求t的值;
(2)当点D在线段AB上运动时,是否始终有DG=GF?若成立,请说明理由;
(3)小扬同学通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图2的情况时,EG的长是否发生变化?若改变,说明理由;若不变,求出EG的长.
25.如图1,在平面直角坐标系中,O为坐标原点,点A(8,0).动点P从A出发以每秒2个单位长度的速度沿线段AO向终点O运动,同时动点Q从O出发以相同速度沿y轴正半轴运动,点P到达点O,两点同时停止运动,设运动时间为t.
(1)当∠OPQ=45°时,请求出运动时间t;
(2)如图2,以PQ为斜边在第一象限作等腰Rt△PQM,设M点坐标为(m,n),请探究m与n的数量关系并说明理由.
26.如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,交AC于D点,且∠ODQ=90°,求D点的坐标.
27.如图,和均为等腰直角三角形,,E在上,P为的中点,交射线于F,连接.
求证:(1)
(2).
答案
一、单选题
D.C.B.B.C.C.C.D.A.D.
二、填空题
11.65°或25°
12.22cm或20cm
13.12
14.50°
15.2
16.5
17.
18.13
19.7
20.60°
21.10
三、解答题
22.(1)解:图中共有个等腰三角形,即.
理由:在中,,
∴,
∴,
∴,
∴ 是等腰三角形;
在中,,
∴,
∴,
∴,
∴是等腰三角形;
在中,,
∴,
∴,
∴,
∴是等腰三角形.
综上所述,图中共有个等腰三角形.
(2)证明:在中,
∵,,
∴,
∴,
∴是等腰三角形.
23.解:∵
∴
∵
∴
∵
∴
∴.
24.解:(1)由题意得:AD=t,则BD=6-t,BF=6+t,
∵DF⊥AB,△ABC是等边三角形,
∴∠BDF=90°,∠B=60°,
∴∠F=30°,
∴BF=2BD,
即,解得:t=2;
(2)始终有DG=GF成立;
理由如下:如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG,∠ADH=∠ABC,
∵△ABC是等边三角形,
∴∠ADH=∠B=∠A=60°,
∴△ADH是等边三角形,
∴DH=AD,
又∵AD=CF,
∴DH=FC,
在△DGH和△FGC中,
∵∠DHG=∠FCG,∠DGH=∠FGC,DH=FC,
∴△DGH≌△FGC(AAS),
∴DG=GF;
(3)如图2,过点F作FH⊥AC于点H.
在△ADE和△CFH中,
∵∠AED=∠FHC=90°,∠A=∠FCH=60°,AD=CF,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
∵∠DEG=∠FHG=90°,∠DGE=∠FGH,DE=FH,
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=EH=AC=3.
25.(1)由题意可知,AP=2t,OQ=2t,
∵A(8,0),OA=8,
∴,
∴OP=,
在Rt△POQ中,
∵∠POQ=90°, ∠OPQ=45°,
∴∠OQP=45°
∴OP=OQ,
∴,
∴,
∴当∠OPQ=45°时,运动时间为2秒;
(2).
理由:如图,过点M作MB⊥x轴于B,作MC⊥y轴于C,则MC=m,MB=n.
∵MB⊥x轴,MC⊥y轴,
∴∠MBP=∠MCQ=90°.
∵∠POQ=90°,
∴∠BMC=90°,
∵△PMQ是等腰直角三角形,
∴MQ=MP,∠PMQ=90°,
∴∠CMQ=∠BMP,
在△MCQ和△MBP中,
,
∴△MCQ≌△MBP(AAS),
∴MC=MB,
∴.
26. 解:连接BO,延长OD,交AB于E,如图:
∵,OD⊥PQ,
∴OE⊥AB,
∵OA=OB=10,OC=6,四边形OABC是直角梯形,
∴CB8,
∴B点坐标(8,6),
又∵A(10,0),点E是AB中点,
∴AB的中点E点坐标为(9,3),
设直线DO的解析式为:y=ax,
即:3=9a,
解得:a,
∴OD的表达式为:,
∵将A(10,0),C(0,6),代入一次函数y=kx+b可列方程:
,
解得:
∴AC的表达式为:,
∵AC、OD交于点D,可得:
解得:,
∴点D的坐标为(,).
27.(1)∵P为的中点,
∴AP=EP,
∵,
∴∠A=∠FEP,
又∵∠APC=∠FPE,
∴ APC FPE,
∴AC=EF;
(2)∵和均为等腰直角三角形,
∴AC=BC,ED=BD,
∵AC=EF,
∴EF=BC,
连接CD,FD,
∵∠DBC=90°,∠ACB=90°,
∴AC∥DB,
∵,
∴AC∥DB∥EF,
∴∠FED=90°,
∵ED=BD,EF=BC,
又∵,,
∴DF=DC,即 DCF是等腰三角形,
∵CP=FP,
∴.
一、单选题
1.△ABC中,AB=AC,D为BC边的中点,以下结论:(1)AD⊥BC; (2)∠B=∠C;(3)AD平分∠BAC,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.若等腰三角形的两边长为3和7,则该等腰三角形的周长为( )
A.10 B.13 C.17 D.13或17
3.等腰三角形的底角等于,则该等腰三角形的顶角度数为( )
A. B. C.或 D.或
4.如图,在中,为BC边上的中线,,则的度数为( )
A. B. C. D.
5.如图,△是等边三角形,是边上的高,且,是的中点,是上的一个动点,则与的和最小是( )
A.3 B.4 C.6 D.8
6.如图,中,,,,,则的度数为( )
A. B. C. D.
7.下列结论中:①有一个外角是的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的等腰三角形是等边三角形;④三个内角都相等的三角形是等边三角形.其中正确的个数是( )
A. B. C. D.
8.如图,在△中,,为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点为圆心,长为半径作圆弧,交于点;③以点为圆心,长为半径作圆弧,交②中所作的圆弧于点;④作射线交于点.下列说法不正确的是( )
A.= B.=∠ACB
C.∠CHB=∠A+∠B D.=∠HCB
9.如图所示,在中,,是边上任意一点,过作于,于,若,,则AB=( )
A.5 B.6 C.7 D.8
10.在网格中作出点P,使△ABP以AB为腰的等腰三角形,且点P要在格点上,则这样的点P的个数是( )
A.6 B.7 C.8 D.9
二、填空题
11.若等腰三角形一腰上的高与另一腰的夹角为,腰长为6,则这个等腰三角形的底角度数是____________.
12.已知等腰三角形的一边等于8 cm,另一边等于6 cm,则此三角形的周长为 _____________.
13.如图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图②,那么在Rt△ABC中,BC=6,则AB=_____.
14.中,,则______.
15.如图,在中,, ,BD平分,交AC于点D,,则点 D到BC的距离是 ________ .
16.如图,在中,和的平分线交于点,过点作交于点,交于点,若,,则的长为________.
17.如图:在中,,,平分,若,则_____.
18.如图,在△ABC中,∠ACB=90°,AC=BC.点D在斜边AB上,以CD为直角边作等腰直角三角形CDE,∠DCE=90°,连结BE.若AD=5,DB=12,则DE的长为_________.
19.如图,是等边三角形,,、相交于点,于,,,则的长是______.
20.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,则的度数是______.
21.如图,在中,,点在延长线上,于点,交于点,若,,则的长度为________.
三、解答题
22.如图,.
(1)写出图中所有的等腰三角形;
(2)选其中一个等腰三角形加以证明.
23.如图,在中,点是上一点,,,求的度数.
24.如图1,在边长为6的等边△ABC中,点D从点A开始在射线AB上运动,速度为1个单位/秒,点F同时从C出发,以相同的速度沿射线BC方向运动,过点D作DE⊥AC,连接DF交射线AC于点G,设点D的运动时间为t秒;
(1)当DF⊥AB时,求t的值;
(2)当点D在线段AB上运动时,是否始终有DG=GF?若成立,请说明理由;
(3)小扬同学通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图2的情况时,EG的长是否发生变化?若改变,说明理由;若不变,求出EG的长.
25.如图1,在平面直角坐标系中,O为坐标原点,点A(8,0).动点P从A出发以每秒2个单位长度的速度沿线段AO向终点O运动,同时动点Q从O出发以相同速度沿y轴正半轴运动,点P到达点O,两点同时停止运动,设运动时间为t.
(1)当∠OPQ=45°时,请求出运动时间t;
(2)如图2,以PQ为斜边在第一象限作等腰Rt△PQM,设M点坐标为(m,n),请探究m与n的数量关系并说明理由.
26.如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,交AC于D点,且∠ODQ=90°,求D点的坐标.
27.如图,和均为等腰直角三角形,,E在上,P为的中点,交射线于F,连接.
求证:(1)
(2).
答案
一、单选题
D.C.B.B.C.C.C.D.A.D.
二、填空题
11.65°或25°
12.22cm或20cm
13.12
14.50°
15.2
16.5
17.
18.13
19.7
20.60°
21.10
三、解答题
22.(1)解:图中共有个等腰三角形,即.
理由:在中,,
∴,
∴,
∴,
∴ 是等腰三角形;
在中,,
∴,
∴,
∴,
∴是等腰三角形;
在中,,
∴,
∴,
∴,
∴是等腰三角形.
综上所述,图中共有个等腰三角形.
(2)证明:在中,
∵,,
∴,
∴,
∴是等腰三角形.
23.解:∵
∴
∵
∴
∵
∴
∴.
24.解:(1)由题意得:AD=t,则BD=6-t,BF=6+t,
∵DF⊥AB,△ABC是等边三角形,
∴∠BDF=90°,∠B=60°,
∴∠F=30°,
∴BF=2BD,
即,解得:t=2;
(2)始终有DG=GF成立;
理由如下:如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG,∠ADH=∠ABC,
∵△ABC是等边三角形,
∴∠ADH=∠B=∠A=60°,
∴△ADH是等边三角形,
∴DH=AD,
又∵AD=CF,
∴DH=FC,
在△DGH和△FGC中,
∵∠DHG=∠FCG,∠DGH=∠FGC,DH=FC,
∴△DGH≌△FGC(AAS),
∴DG=GF;
(3)如图2,过点F作FH⊥AC于点H.
在△ADE和△CFH中,
∵∠AED=∠FHC=90°,∠A=∠FCH=60°,AD=CF,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
∵∠DEG=∠FHG=90°,∠DGE=∠FGH,DE=FH,
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=EH=AC=3.
25.(1)由题意可知,AP=2t,OQ=2t,
∵A(8,0),OA=8,
∴,
∴OP=,
在Rt△POQ中,
∵∠POQ=90°, ∠OPQ=45°,
∴∠OQP=45°
∴OP=OQ,
∴,
∴,
∴当∠OPQ=45°时,运动时间为2秒;
(2).
理由:如图,过点M作MB⊥x轴于B,作MC⊥y轴于C,则MC=m,MB=n.
∵MB⊥x轴,MC⊥y轴,
∴∠MBP=∠MCQ=90°.
∵∠POQ=90°,
∴∠BMC=90°,
∵△PMQ是等腰直角三角形,
∴MQ=MP,∠PMQ=90°,
∴∠CMQ=∠BMP,
在△MCQ和△MBP中,
,
∴△MCQ≌△MBP(AAS),
∴MC=MB,
∴.
26. 解:连接BO,延长OD,交AB于E,如图:
∵,OD⊥PQ,
∴OE⊥AB,
∵OA=OB=10,OC=6,四边形OABC是直角梯形,
∴CB8,
∴B点坐标(8,6),
又∵A(10,0),点E是AB中点,
∴AB的中点E点坐标为(9,3),
设直线DO的解析式为:y=ax,
即:3=9a,
解得:a,
∴OD的表达式为:,
∵将A(10,0),C(0,6),代入一次函数y=kx+b可列方程:
,
解得:
∴AC的表达式为:,
∵AC、OD交于点D,可得:
解得:,
∴点D的坐标为(,).
27.(1)∵P为的中点,
∴AP=EP,
∵,
∴∠A=∠FEP,
又∵∠APC=∠FPE,
∴ APC FPE,
∴AC=EF;
(2)∵和均为等腰直角三角形,
∴AC=BC,ED=BD,
∵AC=EF,
∴EF=BC,
连接CD,FD,
∵∠DBC=90°,∠ACB=90°,
∴AC∥DB,
∵,
∴AC∥DB∥EF,
∴∠FED=90°,
∵ED=BD,EF=BC,
又∵,,
∴DF=DC,即 DCF是等腰三角形,
∵CP=FP,
∴.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
