七年级数学上册试题 1.2展开与折叠同步练习-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 1.2展开与折叠同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 17:51:04 | ||
图片预览

文档简介
1.2展开与折叠
第一课时
一.选择题。
1.将正方体展开需要剪开的棱数为( )
A.5条 B.6条 C.7条 D.8条
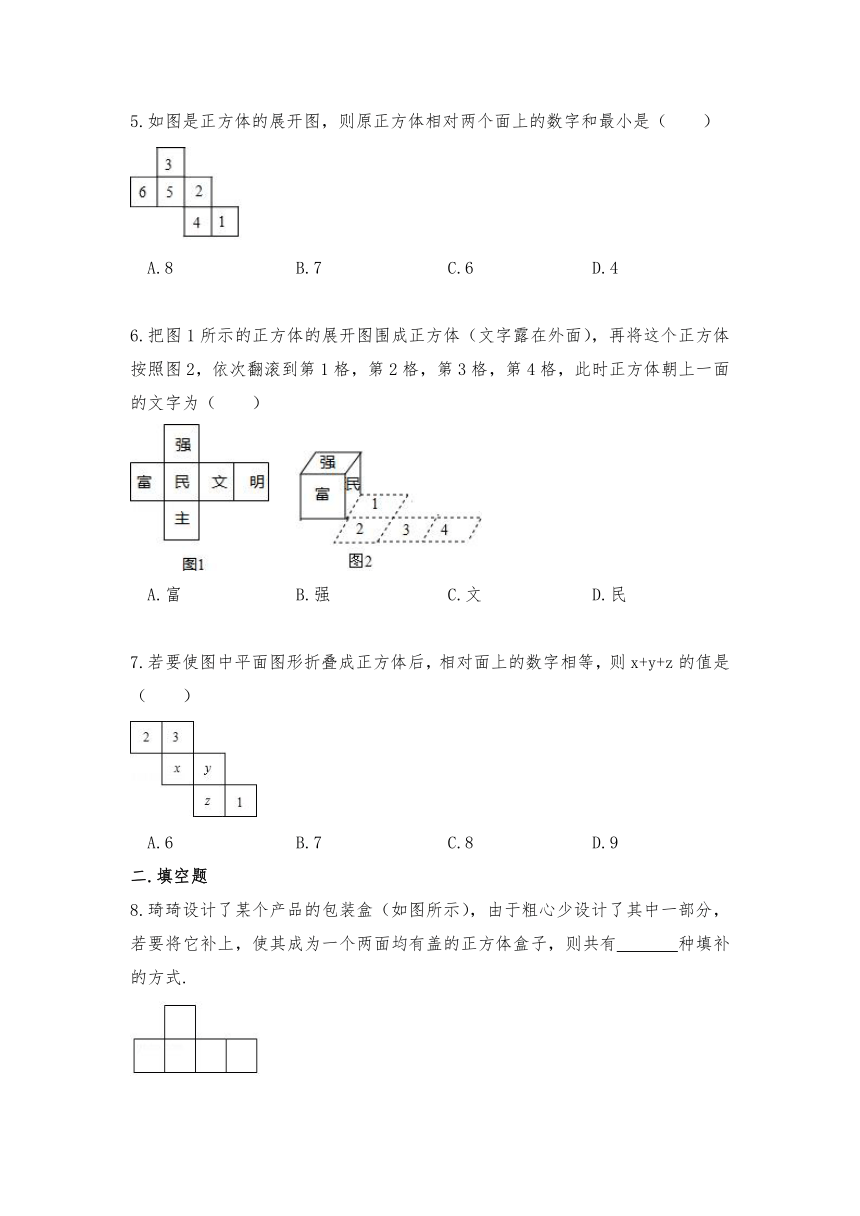
2.观察下列图形,其中不是正方体的表面展开图的是( )
A. B.
C. D.
3.一个正方体的展开图如图所示,若从正方体的右面看是“丽”,“美”在后面,则正方体的上面是( )
A.热 B.爱 C.渭 D.滨
4.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
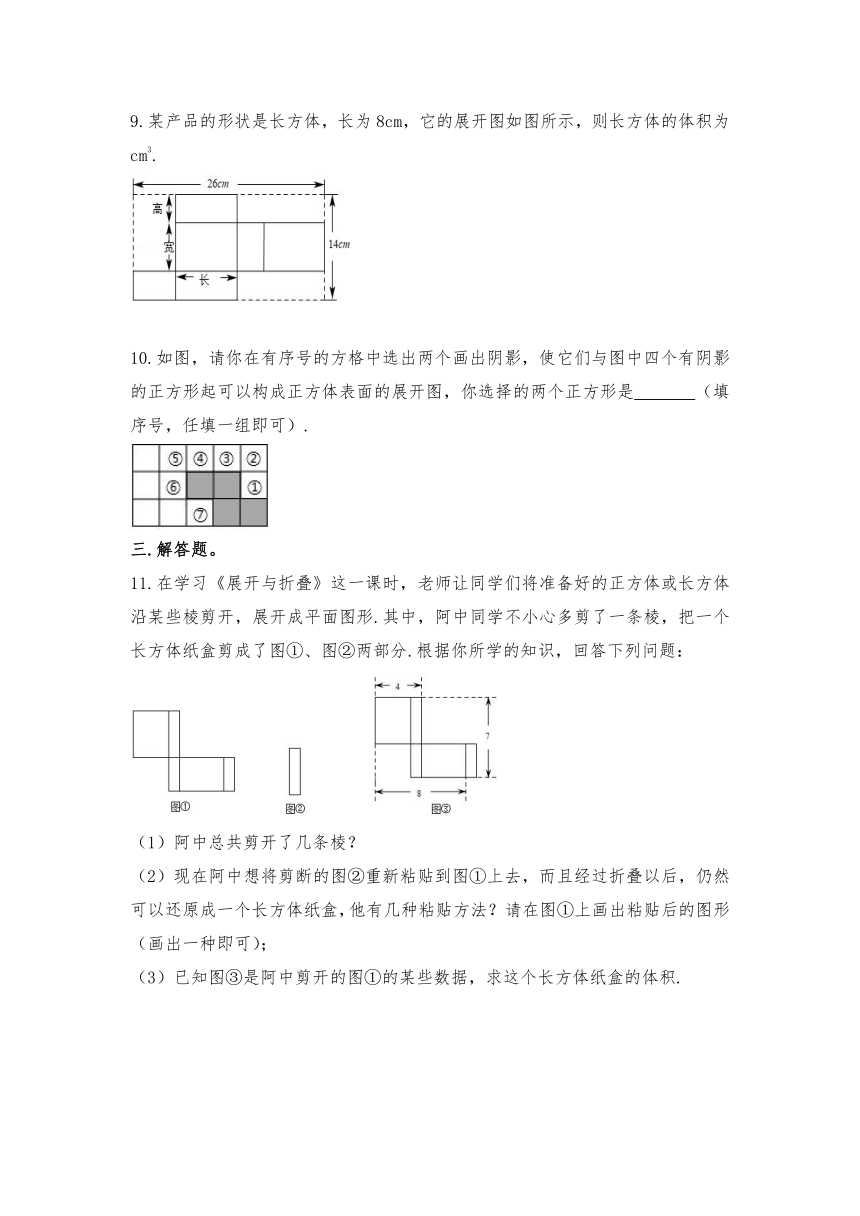
5.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8 B.7 C.6 D.4
6.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A.富 B.强 C.文 D.民
7.若要使图中平面图形折叠成正方体后,相对面上的数字相等,则x+y+z的值是( )
A.6 B.7 C.8 D.9
二.填空题
8.琦琦设计了某个产品的包装盒(如图所示),由于粗心少设计了其中一部分,若要将它补上,使其成为一个两面均有盖的正方体盒子,则共有 种填补的方式.
9.某产品的形状是长方体,长为8cm,它的展开图如图所示,则长方体的体积为 cm3.
10.如图,请你在有序号的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形起可以构成正方体表面的展开图,你选择的两个正方形是 (填序号,任填一组即可).
三.解答题。
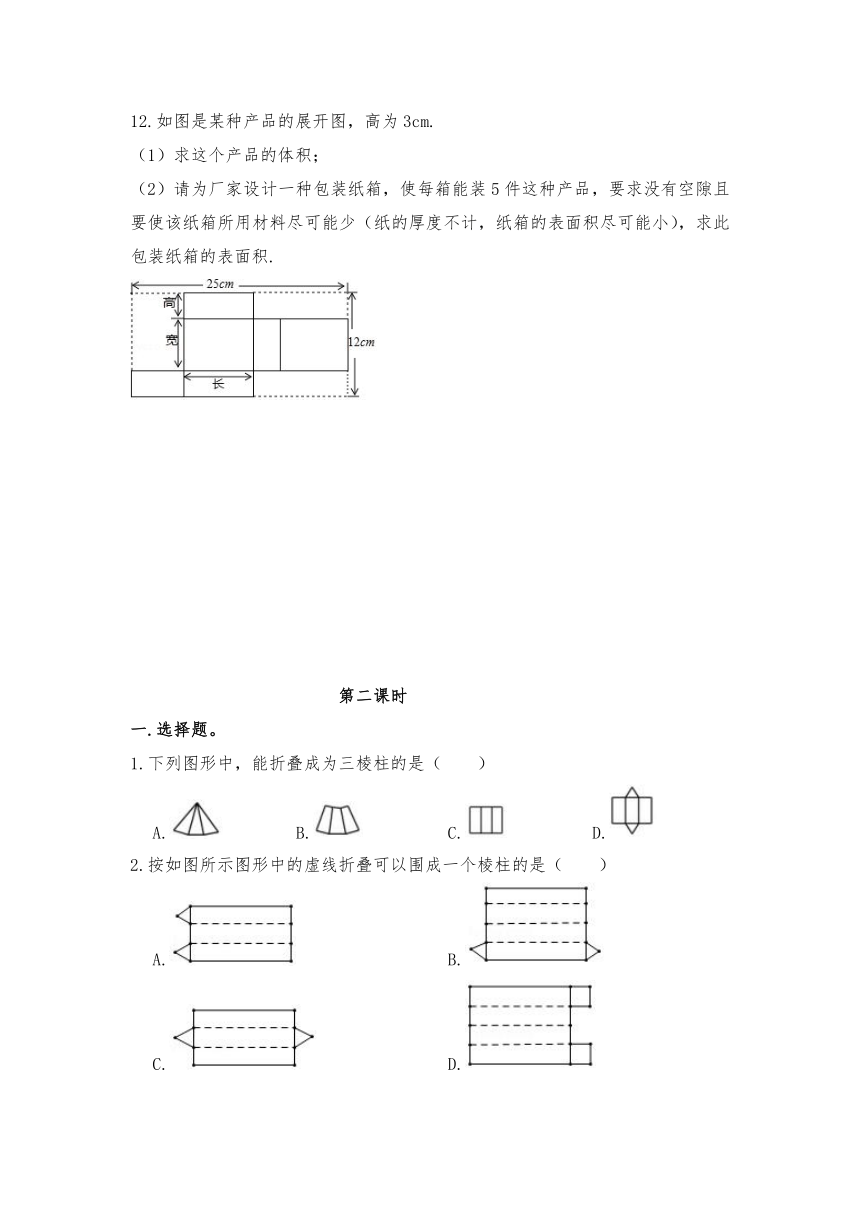
11.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
12.如图是某种产品的展开图,高为3cm.
(1)求这个产品的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此包装纸箱的表面积.
第二课时
一.选择题。
1.下列图形中,能折叠成为三棱柱的是( )
A. B. C. D.
2.按如图所示图形中的虚线折叠可以围成一个棱柱的是( )
A. B.
C. D.
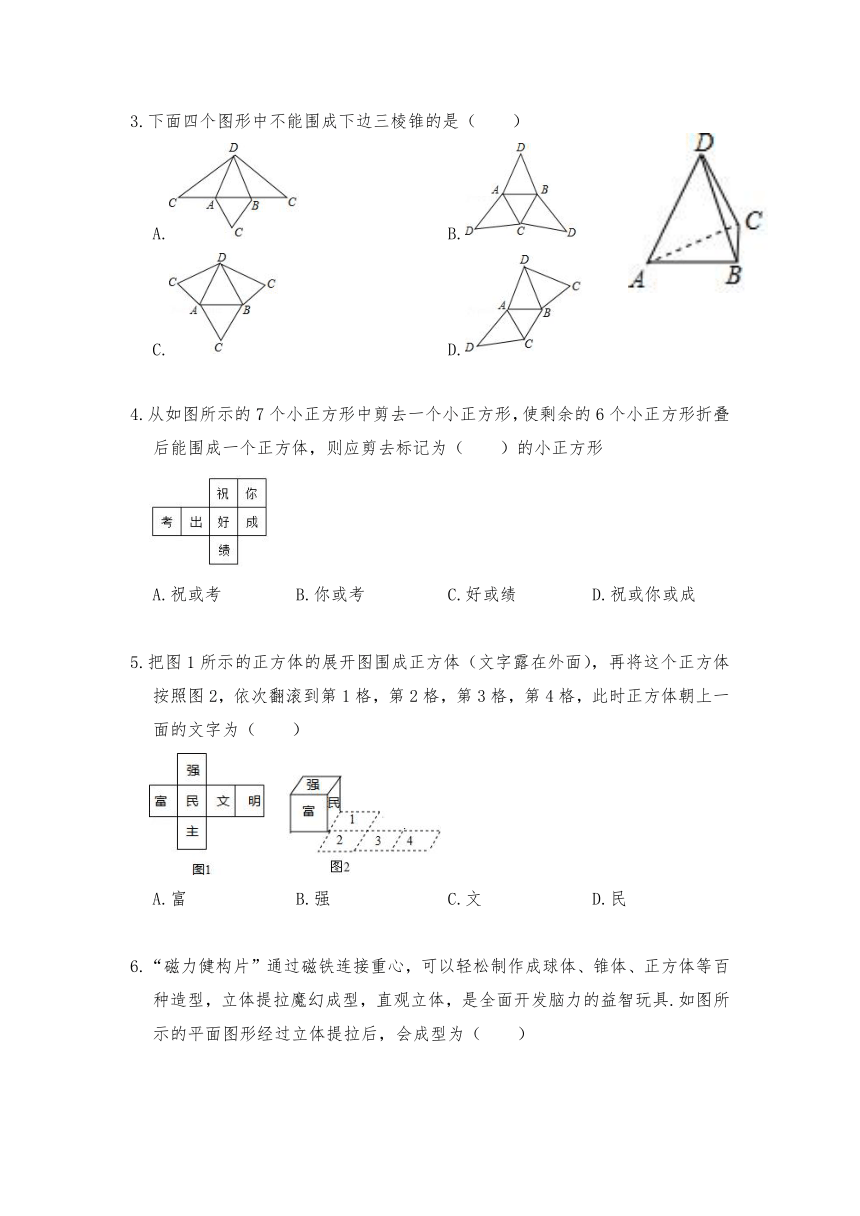
3.下面四个图形中不能围成下边三棱锥的是( )
A. B.
C. D.
4.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考 B.你或考 C.好或绩 D.祝或你或成
5.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A.富 B.强 C.文 D.民
6.“磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
A.圆锥 B.长方体 C.五棱柱 D.圆柱
7.如图是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )
A.1000cm3 B.1500cm3 C.2000cm3 D.2500cm3
8.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
二.填空题。
9.如图,①~④展开图中,能围成三棱柱的是 .
10.如图,把某直三棱柱的表面展开图围成三棱柱后与A重合的字母是 .
11.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体.在下图中适合按要求加上小正方形的位置有 个.
12.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是 .
三.解答题。
13.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
14.仓库里有以下四种规格数量足够多的长方形、正方形的铁片(尺寸单位:分米):
从中选5块铁片,焊接成一个无盖的长方体(或正方体)铁盒(不浪费材料),甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的铁盒,乙型盒是容积最小的铁盒.
(1)甲型盒的容积为: 分米3;乙型盒的容积为: 分米3;(直接写出答案)
(2)现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度是多少分米?
第一课时答案
一.选择题。
C.B.C.C.C.A.A.
二.填空题。
8.4
9.192.
10.④⑤或④⑥或⑤⑥或③⑥.
三.解答题
11.解:(1)总共12条棱,其中有4条未剪开,故阿中总共剪开了8条棱.
(2)答:有4种粘贴方法.
如图,四种情况:
(3)设高为xcm,则宽为(4﹣x)cm,长为[7﹣(4﹣x)]=(3+x)cm,
∴4+(3+x)=8,
解得:x=1,
∴体积为:(3+1)×(4﹣1)×1=12cm3,
答:这个长方形纸盒的体积为12cm3.
12.解:(1)长方体的高为3cm,则长方形的宽为(12﹣2×3)cm,长为(25﹣3﹣6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),
8×15=120(cm2)
6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).
第二课时答案
一.选择题。
D.C.A.D.A.C.A.C.
二.填空题
9.②.
10.M和D.
11.4.
12.1和7;
三.解答题
13.解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
14.解:(1)∵甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的,
∴甲盒的长为2分米,宽为4分米,高为5分米,
∴甲型盒容积为2×4×5=40分米3;
乙型盒容积最小,即长、宽、高最小,因此乙盒为长、宽、高均为2分米的正方体,体积为2×2×2=8立方分米,
故答案为40,8.
(2)甲盒的底面积为:2×4=8平方分米,两个乙盒的水的体积为8×2=16立方分米,
甲盒内水的高度为:16÷8=2分米,
答:甲型盒中水的高度是 2 分米.
第一课时
一.选择题。
1.将正方体展开需要剪开的棱数为( )
A.5条 B.6条 C.7条 D.8条
2.观察下列图形,其中不是正方体的表面展开图的是( )
A. B.
C. D.
3.一个正方体的展开图如图所示,若从正方体的右面看是“丽”,“美”在后面,则正方体的上面是( )
A.热 B.爱 C.渭 D.滨
4.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
5.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8 B.7 C.6 D.4
6.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A.富 B.强 C.文 D.民
7.若要使图中平面图形折叠成正方体后,相对面上的数字相等,则x+y+z的值是( )
A.6 B.7 C.8 D.9
二.填空题
8.琦琦设计了某个产品的包装盒(如图所示),由于粗心少设计了其中一部分,若要将它补上,使其成为一个两面均有盖的正方体盒子,则共有 种填补的方式.
9.某产品的形状是长方体,长为8cm,它的展开图如图所示,则长方体的体积为 cm3.
10.如图,请你在有序号的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形起可以构成正方体表面的展开图,你选择的两个正方形是 (填序号,任填一组即可).
三.解答题。
11.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
12.如图是某种产品的展开图,高为3cm.
(1)求这个产品的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此包装纸箱的表面积.
第二课时
一.选择题。
1.下列图形中,能折叠成为三棱柱的是( )
A. B. C. D.
2.按如图所示图形中的虚线折叠可以围成一个棱柱的是( )
A. B.
C. D.
3.下面四个图形中不能围成下边三棱锥的是( )
A. B.
C. D.
4.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
A.祝或考 B.你或考 C.好或绩 D.祝或你或成
5.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A.富 B.强 C.文 D.民
6.“磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
A.圆锥 B.长方体 C.五棱柱 D.圆柱
7.如图是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )
A.1000cm3 B.1500cm3 C.2000cm3 D.2500cm3
8.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
二.填空题。
9.如图,①~④展开图中,能围成三棱柱的是 .
10.如图,把某直三棱柱的表面展开图围成三棱柱后与A重合的字母是 .
11.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体.在下图中适合按要求加上小正方形的位置有 个.
12.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是 .
三.解答题。
13.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
14.仓库里有以下四种规格数量足够多的长方形、正方形的铁片(尺寸单位:分米):
从中选5块铁片,焊接成一个无盖的长方体(或正方体)铁盒(不浪费材料),甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的铁盒,乙型盒是容积最小的铁盒.
(1)甲型盒的容积为: 分米3;乙型盒的容积为: 分米3;(直接写出答案)
(2)现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度是多少分米?
第一课时答案
一.选择题。
C.B.C.C.C.A.A.
二.填空题。
8.4
9.192.
10.④⑤或④⑥或⑤⑥或③⑥.
三.解答题
11.解:(1)总共12条棱,其中有4条未剪开,故阿中总共剪开了8条棱.
(2)答:有4种粘贴方法.
如图,四种情况:
(3)设高为xcm,则宽为(4﹣x)cm,长为[7﹣(4﹣x)]=(3+x)cm,
∴4+(3+x)=8,
解得:x=1,
∴体积为:(3+1)×(4﹣1)×1=12cm3,
答:这个长方形纸盒的体积为12cm3.
12.解:(1)长方体的高为3cm,则长方形的宽为(12﹣2×3)cm,长为(25﹣3﹣6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),
8×15=120(cm2)
6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).
第二课时答案
一.选择题。
D.C.A.D.A.C.A.C.
二.填空题
9.②.
10.M和D.
11.4.
12.1和7;
三.解答题
13.解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
14.解:(1)∵甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的,
∴甲盒的长为2分米,宽为4分米,高为5分米,
∴甲型盒容积为2×4×5=40分米3;
乙型盒容积最小,即长、宽、高最小,因此乙盒为长、宽、高均为2分米的正方体,体积为2×2×2=8立方分米,
故答案为40,8.
(2)甲盒的底面积为:2×4=8平方分米,两个乙盒的水的体积为8×2=16立方分米,
甲盒内水的高度为:16÷8=2分米,
答:甲型盒中水的高度是 2 分米.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
