一元二次方程复习[上学期]
文档属性
| 名称 | 一元二次方程复习[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 623.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-04 11:58:00 | ||
图片预览






文档简介
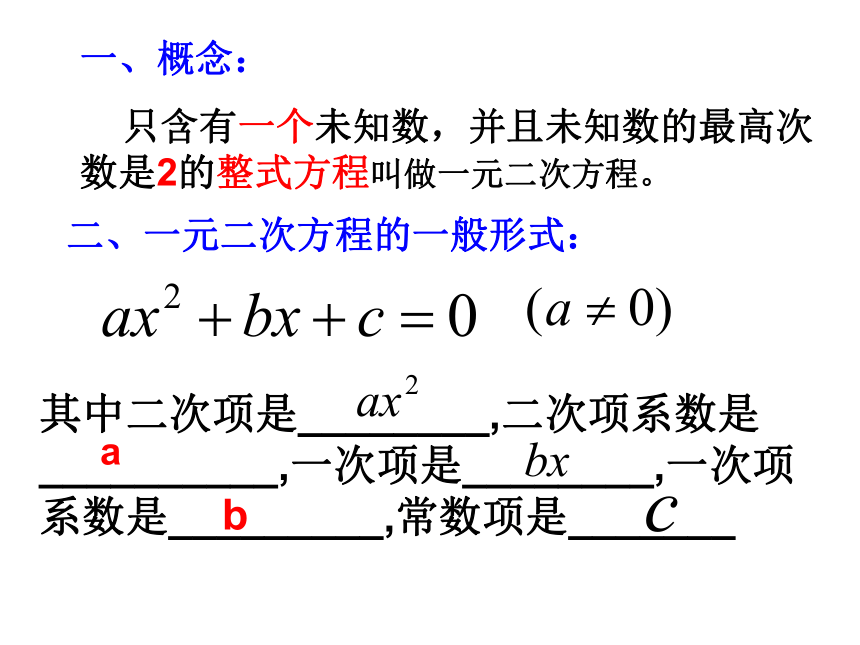
课件23张PPT。一元二次方程复习课章安中学 何贤才一元二次方程定义解法应用一、概念: 只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。二、一元二次方程的一般形式:其中二次项是________,二次项系数是__________,一次项是________,一次项系数是_________,常数项是_______ab1、判断下面哪些方程是一元二次方程
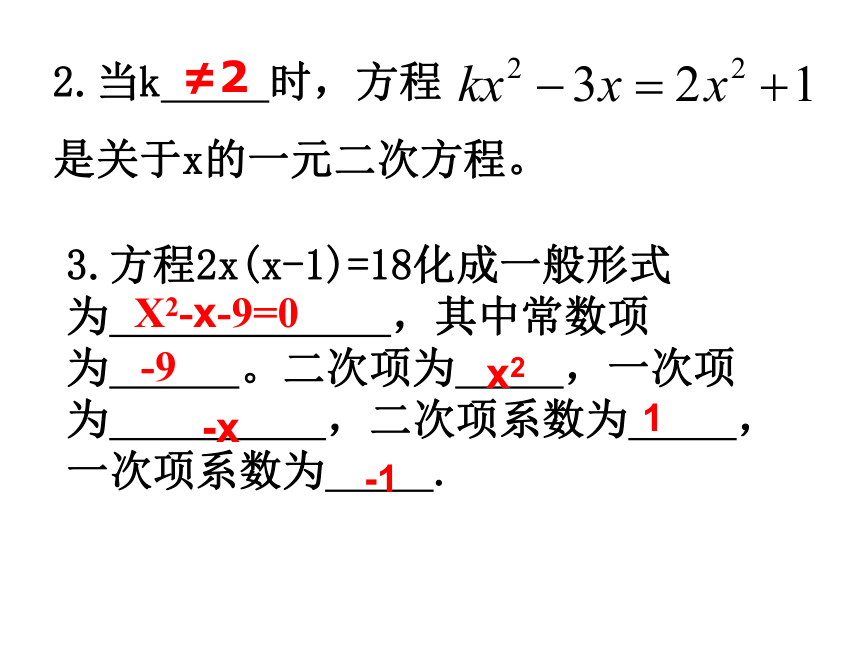
√ √ × × × × 练习一2.当k 时,方程
是关于x的一元二次方程。≠23.方程2x(x-1)=18化成一般形式为 ,其中常数项为 。二次项为 ,一次项为 ,二次项系数为 ,一次项系数为 .X2-x-9=0-9x21-1-x三、方程的根能使方程左右两边相等的未知数的值叫做方程的解,一元二次方程的解也叫做一元二次方程的根
1.已知x=-1是方程x2-ax+6=0的一个根,则a=___另一个根为__
2.若关于X的一元二次方程
的一个根为0,则 的值为( )
练习二A、1 B、 C、 1或 D、3、一元二次方程ax2 +bx +c =0,
若x=1是它的一个根,则a+b+c= ,
若a -b+c=0,则方程必有一根为 。
0-1-7-6B(1)直接开平方法(2)配方法(3)公式法(4)因式分解法四、一元二次方程的解法例:解下列方程(1)实例讲解一元二次方程的解法:解: 注:当一元二次方程缺一次项时常用直接开平方法。(直接开平方法)例:(2)实例讲解一元二次方程的解法:解: 注:当一元二次方程二次项系数为1且一次项系数为偶数时常用配方法比较简便。(配方法)——配方法解一元二次方程的解题过程1. 把方程化成一元二次方程的一般形式
2. 把二次项系数化为1
3. 把含有未知数的项放在方程的左边,不含未知 数的项放在方程的右边。
4. 方程的两边同加上一次项系数一半的平方
5. 方程的左边化成完全平方的形式,方程的右边化成非负数
6. 利用直接开平方的方法去解例:(3)实例讲解一元二次方程的解法:解:(公式法)公式法解一元二次方程的解题过程
1. 把方程化成一元二次方程的一般形式
写出方程各项的系数(系数包括前面符号)
计算出b2-4ac的值,看b2-4ac的值与0的关系,若b2-4ac的值小于0,则此方程没有实数根 。
当b2-4ac的值大于、等于0时, 代入求根公式 计算出方程的解
一元二次方程的解法(因式分解法) 解:原方程化为 (y+2) 2﹣3(y+2)=0
(y+2)(y+2-3)=0
(y+2)(y-1)=0
y+2=0 或 y-1=0
∴y1=-2 y2=1把y+2看作一个整体,变成
(ax+b)(cx+d)=0形式。 实例讲解例:(4)因式分解法的解题过程移项,使方程的右边为0。
将方程左边分解因式 。
令每个因式分别为零,得到两个一元一次方程。
解这两个一元一次方程,它们的解就是原方程的解。练习三跳跳,看看你能跳多高?
(1)关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论
m取何值,此方程都是一元二次方程。(2)代数式2x2-8x+9何时能取得最小值,最小值是多少?1.配方问题2、解方程:x2-5∣x∣-6=0解:当x≥0时,原方程化为
解得:当x<0时,原方程化为
解得:∴原方程解为检查你的复习效果:1、用配方法解方程2x2 +4x +1 =0,配方后得到的方程是 __________
2、请写出一个根为 ,另一个根满足 的一元二次方程 ___________
2(x+1)2=1
3.一元二次方程3x2=2x的解是 .4.一元二次方程(m-2)x2+3x+m2-4=0有一解为0,则m的值是 .5.已知m是方程x2-x-2=0的一个根,那么代数式m2-m = .x1=0,x2=m=-222拓展练习:请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程 ,我们可以将x2-1视为一个整体,然后设x2-1=y,则原方程可化为y2-5y+4=0 ①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2,x=± .当y=4时,x2-1=4,∴x2=5,x=± . ∴原方程的解为x1= ,x2=- ,x3= ,x4=- .解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_______法达到了降次的目的,体现了_________的数学思想.
(2)解方程换元法转化小结: 本节课我们主要复习了一元二次方程的定义和解法,要求大家掌握以下几点:
1、会判断一个方程是不是一元二次方程,能够熟练地将一元二次方程化为一般形式,并准确地写出其各项的系数。
2、能灵活运用一元二次方程的四种基本解法求方程的解。
3、能根据方程根的定义解决有关问题。 谢谢大家
欢迎批评指正
多提宝贵意见
√ √ × × × × 练习一2.当k 时,方程
是关于x的一元二次方程。≠23.方程2x(x-1)=18化成一般形式为 ,其中常数项为 。二次项为 ,一次项为 ,二次项系数为 ,一次项系数为 .X2-x-9=0-9x21-1-x三、方程的根能使方程左右两边相等的未知数的值叫做方程的解,一元二次方程的解也叫做一元二次方程的根
1.已知x=-1是方程x2-ax+6=0的一个根,则a=___另一个根为__
2.若关于X的一元二次方程
的一个根为0,则 的值为( )
练习二A、1 B、 C、 1或 D、3、一元二次方程ax2 +bx +c =0,
若x=1是它的一个根,则a+b+c= ,
若a -b+c=0,则方程必有一根为 。
0-1-7-6B(1)直接开平方法(2)配方法(3)公式法(4)因式分解法四、一元二次方程的解法例:解下列方程(1)实例讲解一元二次方程的解法:解: 注:当一元二次方程缺一次项时常用直接开平方法。(直接开平方法)例:(2)实例讲解一元二次方程的解法:解: 注:当一元二次方程二次项系数为1且一次项系数为偶数时常用配方法比较简便。(配方法)——配方法解一元二次方程的解题过程1. 把方程化成一元二次方程的一般形式
2. 把二次项系数化为1
3. 把含有未知数的项放在方程的左边,不含未知 数的项放在方程的右边。
4. 方程的两边同加上一次项系数一半的平方
5. 方程的左边化成完全平方的形式,方程的右边化成非负数
6. 利用直接开平方的方法去解例:(3)实例讲解一元二次方程的解法:解:(公式法)公式法解一元二次方程的解题过程
1. 把方程化成一元二次方程的一般形式
写出方程各项的系数(系数包括前面符号)
计算出b2-4ac的值,看b2-4ac的值与0的关系,若b2-4ac的值小于0,则此方程没有实数根 。
当b2-4ac的值大于、等于0时, 代入求根公式 计算出方程的解
一元二次方程的解法(因式分解法) 解:原方程化为 (y+2) 2﹣3(y+2)=0
(y+2)(y+2-3)=0
(y+2)(y-1)=0
y+2=0 或 y-1=0
∴y1=-2 y2=1把y+2看作一个整体,变成
(ax+b)(cx+d)=0形式。 实例讲解例:(4)因式分解法的解题过程移项,使方程的右边为0。
将方程左边分解因式 。
令每个因式分别为零,得到两个一元一次方程。
解这两个一元一次方程,它们的解就是原方程的解。练习三跳跳,看看你能跳多高?
(1)关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论
m取何值,此方程都是一元二次方程。(2)代数式2x2-8x+9何时能取得最小值,最小值是多少?1.配方问题2、解方程:x2-5∣x∣-6=0解:当x≥0时,原方程化为
解得:当x<0时,原方程化为
解得:∴原方程解为检查你的复习效果:1、用配方法解方程2x2 +4x +1 =0,配方后得到的方程是 __________
2、请写出一个根为 ,另一个根满足 的一元二次方程 ___________
2(x+1)2=1
3.一元二次方程3x2=2x的解是 .4.一元二次方程(m-2)x2+3x+m2-4=0有一解为0,则m的值是 .5.已知m是方程x2-x-2=0的一个根,那么代数式m2-m = .x1=0,x2=m=-222拓展练习:请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程 ,我们可以将x2-1视为一个整体,然后设x2-1=y,则原方程可化为y2-5y+4=0 ①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2,x=± .当y=4时,x2-1=4,∴x2=5,x=± . ∴原方程的解为x1= ,x2=- ,x3= ,x4=- .解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_______法达到了降次的目的,体现了_________的数学思想.
(2)解方程换元法转化小结: 本节课我们主要复习了一元二次方程的定义和解法,要求大家掌握以下几点:
1、会判断一个方程是不是一元二次方程,能够熟练地将一元二次方程化为一般形式,并准确地写出其各项的系数。
2、能灵活运用一元二次方程的四种基本解法求方程的解。
3、能根据方程根的定义解决有关问题。 谢谢大家
欢迎批评指正
多提宝贵意见
同课章节目录
