26.2.5求函数的解析式[下学期]
文档属性
| 名称 | 26.2.5求函数的解析式[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 251.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-04 00:00:00 | ||
图片预览



文档简介
课件17张PPT。26.2.3 求二次函数的函数关系式(1)一般式(2)顶点式顶点坐标(h,k)二次函数的解析式有哪些?问题2
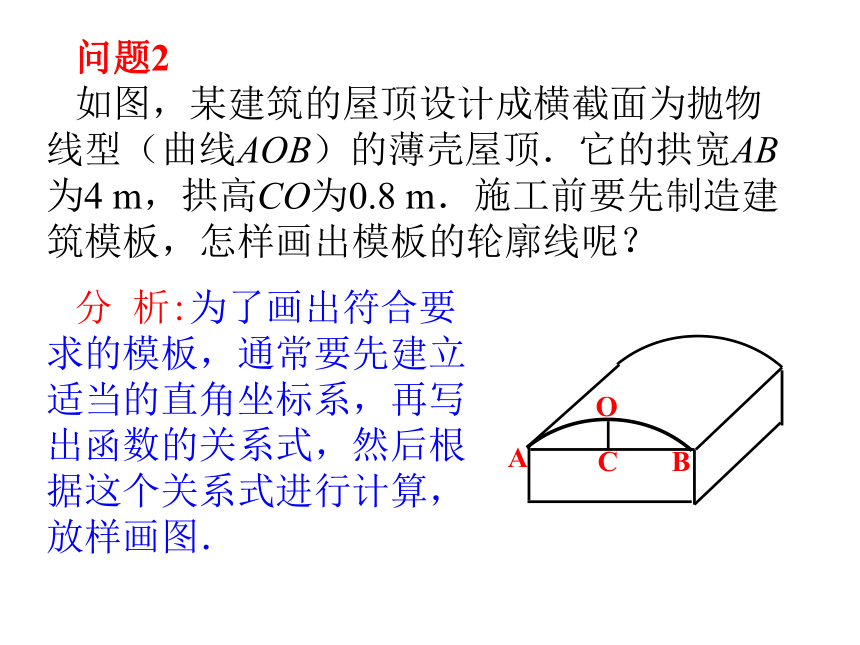
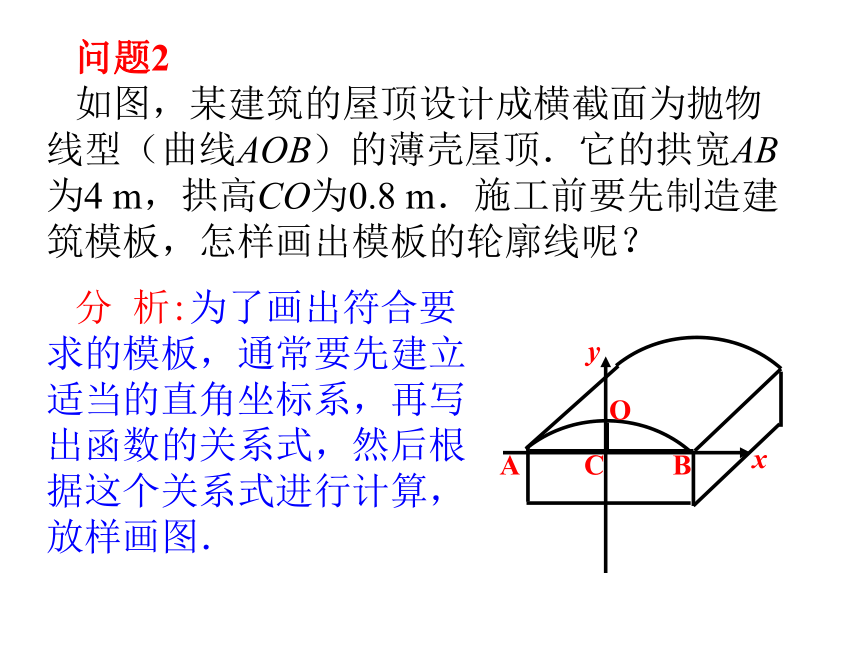
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
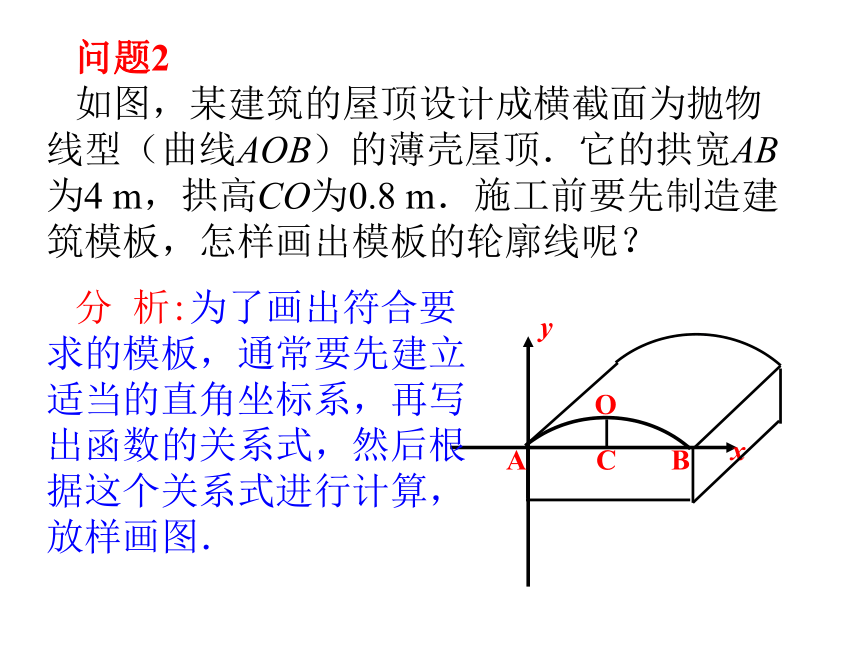
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.(0,–0.8)(–2,–0.8)(2,–0.8)分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?例1.已知:二次函数的图像经过点A(–1,6)、B(3,0)、C(0,3),求这个函数的解析式。解:设所求函数解析式为y=ax2+bx+c .由已知函数图象过(-1,6),(3,0),(0,3)三点得 解这个方程组得a= 0.5,b= – 2.5,c=3 ∴所求得的函数解析式为y=0.5x2 – 2.5x+3例2.已知:抛物线y=ax2+bx+c过直线 与x轴、y轴的交点,且过(1,1),求抛物线的解析式.分析:例3.已知:二次函数的图像的对称轴为直线
x= –3,并且函数有最大值为5,图像经过点
(–1,–3),求这个函数的解析式。 解:由题意可知,该函数的顶点的坐标是(-3,5), 所以,设y=a(x+3)2+5又抛物线经过点(-1,-3),得 -3=a(-1+3)2+5 ∴ a=-2∴所求的函数解析式为:y= –2(x+3)2+5即y= –2x2–12x–13例4.已知:二次函数的图像的顶点的坐标是(1,4),并且抛物线与x轴的两个交点的距离是4,求这个函数的解析式。 A B x=1(1)一般式(2)顶点式顶点坐标(h,k)二次函数的解析式有哪些?*例5.已知:如图,求二次函数解析式y=ax2+bx+c.解:如图,由题意得:抛物线与x轴交点的横坐标为-1和3∴设所求函数解析式为y=a(x+1)(x-3)∵图象过点(0,3)∴3=a(0+1)(0-3) ∴a=-1∴所求的函数解析式为y=-(x+1)(x-3) 即y= –x2+2x+3例6.已知:抛物线与坐标轴交于A,B,C三个点,其中A的坐标为(-1,0),B的坐标为(3,0),并且△ABC的面积是6,求这个函数的解析式。 分析:由题意可知OC的长是3,所以点C的坐标为(0,3)或(0,-3)当C(0,3)时,函数的解析式为:
y=-x2+2x+3 当C(0,-3)时,函数的解析式为: -y=-x2+2x+3,即y=x2-2x-3 二次函数解析式的确定:归纳小结二次函数解析式的确定:归纳小结(3)过与x轴的两个交点和一普通点的二次函数解析式确定.
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.(0,–0.8)(–2,–0.8)(2,–0.8)分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.问题2
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?例1.已知:二次函数的图像经过点A(–1,6)、B(3,0)、C(0,3),求这个函数的解析式。解:设所求函数解析式为y=ax2+bx+c .由已知函数图象过(-1,6),(3,0),(0,3)三点得 解这个方程组得a= 0.5,b= – 2.5,c=3 ∴所求得的函数解析式为y=0.5x2 – 2.5x+3例2.已知:抛物线y=ax2+bx+c过直线 与x轴、y轴的交点,且过(1,1),求抛物线的解析式.分析:例3.已知:二次函数的图像的对称轴为直线
x= –3,并且函数有最大值为5,图像经过点
(–1,–3),求这个函数的解析式。 解:由题意可知,该函数的顶点的坐标是(-3,5), 所以,设y=a(x+3)2+5又抛物线经过点(-1,-3),得 -3=a(-1+3)2+5 ∴ a=-2∴所求的函数解析式为:y= –2(x+3)2+5即y= –2x2–12x–13例4.已知:二次函数的图像的顶点的坐标是(1,4),并且抛物线与x轴的两个交点的距离是4,求这个函数的解析式。 A B x=1(1)一般式(2)顶点式顶点坐标(h,k)二次函数的解析式有哪些?*例5.已知:如图,求二次函数解析式y=ax2+bx+c.解:如图,由题意得:抛物线与x轴交点的横坐标为-1和3∴设所求函数解析式为y=a(x+1)(x-3)∵图象过点(0,3)∴3=a(0+1)(0-3) ∴a=-1∴所求的函数解析式为y=-(x+1)(x-3) 即y= –x2+2x+3例6.已知:抛物线与坐标轴交于A,B,C三个点,其中A的坐标为(-1,0),B的坐标为(3,0),并且△ABC的面积是6,求这个函数的解析式。 分析:由题意可知OC的长是3,所以点C的坐标为(0,3)或(0,-3)当C(0,3)时,函数的解析式为:
y=-x2+2x+3 当C(0,-3)时,函数的解析式为: -y=-x2+2x+3,即y=x2-2x-3 二次函数解析式的确定:归纳小结二次函数解析式的确定:归纳小结(3)过与x轴的两个交点和一普通点的二次函数解析式确定.
