四边形整理与探究[下学期]
图片预览




文档简介
课件20张PPT。四边形
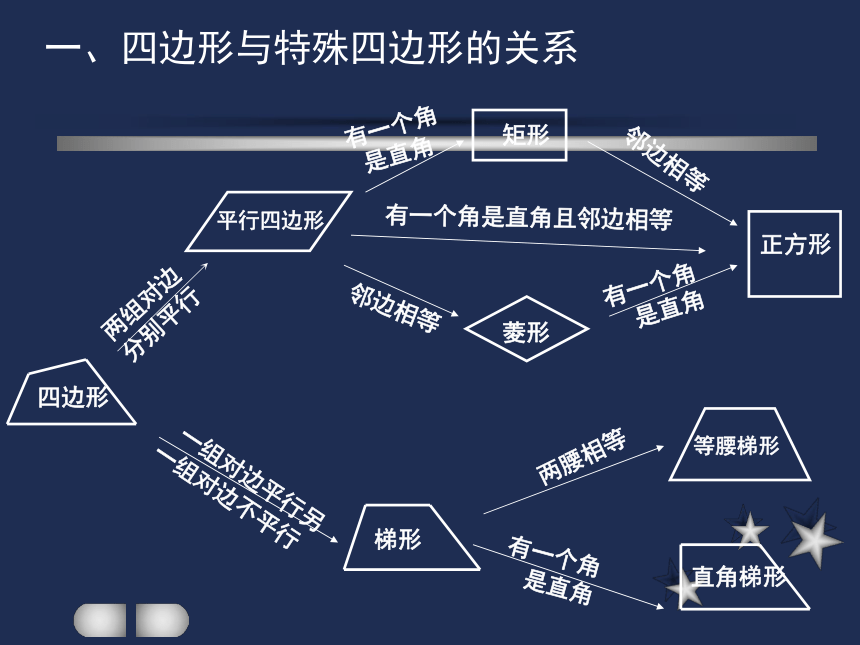
整理与探究一、四边形与特殊四边形的关系四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边
分别平行有一个角
是直角邻边相等邻边相等有一个角
是直角 一组对边平行另
一组对边不平行两腰相等 有一个角
是直角有一个角是直角且邻边相等二、几种特殊四边形的常用判定方法 平行
四边形(1)两组对边分别平行(2)一组对边平行且相等(3)两组
对边分别相等 (4)两组对角分别相等(5)对角线互相平分矩 形(1)有三个角是直角;(2)有一个角是直角的平行四边形;(3)两条对角线相等且平分的四边形。 菱 形(1)四条边都相等;(2)有一组邻边相等的平行四边形;(3)两条对角线互相垂直平分。正方形(1)有一组邻边相等的矩形;(2)有一个角是直角的菱形。等 腰
梯 形(1)同一条底边上的两个内角相等的梯形;(2)两条对角线相等的梯形。三、几种特殊四边形的性质平行
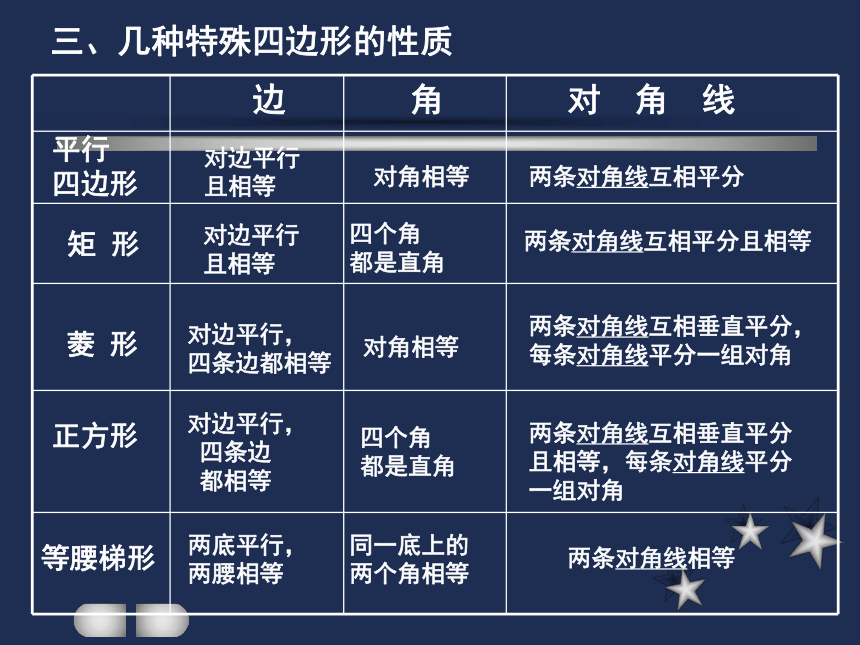
四边形矩 形菱 形正方形等腰梯形边对边平行
且相等对边平行
且相等对边平行,
四条边都相等对边平行,
四条边
都相等两底平行,
两腰相等角对角相等四个角
都是直角对角相等四个角
都是直角同一底上的
两个角相等对 角 线两条对角线互相平分两条对角线互相平分且相等两条对角线互相垂直平分,
每条对角线平分一组对角两条对角线互相垂直平分
且相等,每条对角线平分
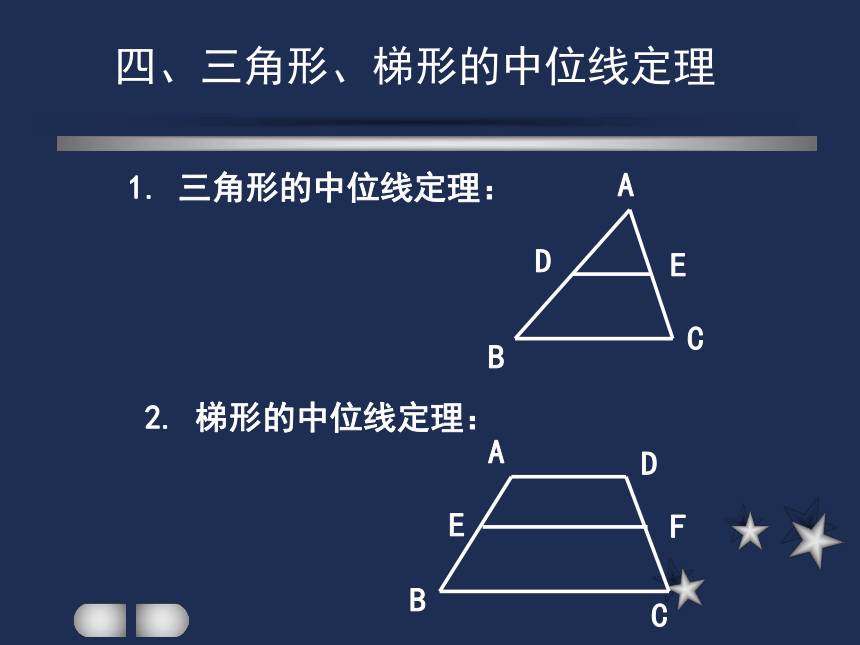
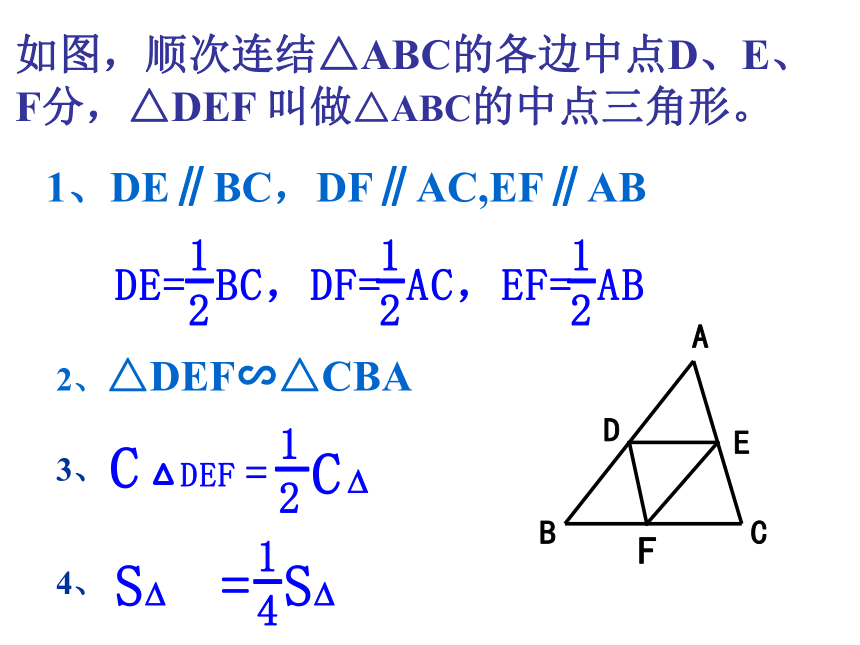
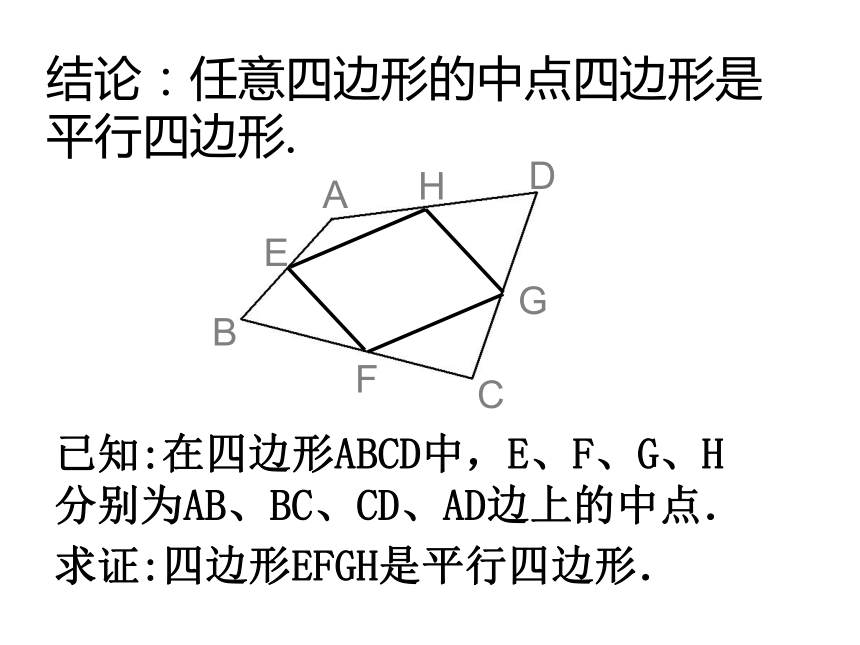
一组对角两条对角线相等C如图,顺次连结△ABC的各边中点D、E、F分,△DEF 叫做△ABC的中点三角形。2、△DEF∽△CBA3、4、1、DE∥BC,DF∥AC,EF∥ABF中点四边形知识探究( 顺次连结四边形各边中点所组成的四边形称为中点四边形)猜想:顺次连结四边形各边中点所组成的四边形是怎样的图形?已知:在四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD边上的中点.求证:四边形EFGH是平行四边形.结论:任意四边形的中点四边形是平行四边形. 如果我们改变四边形ABCD的形状,那么,对于它的中点四边形,又是怎样的图形呢?探索,我能发现 平行四边形、矩形、菱形、梯形、等腰梯形的中点四边形是怎样的图形?1、探索:平行四边形ABCD的中点四边形EFGH是怎样的图形?ABCHDEFG2、菱形、矩形、正方形的中点四边形3、梯形、等腰梯形的中点四边形求证:等腰梯形的中点四边形是菱形。平行四边形的中点四边形为_____________;
矩形的中点四边形为________;
菱形的中点四边形为________;
正方形的中点四边形为________;
梯形的中点四边形为_____________;
等腰梯形的中点四边形为________。探索,我的发现平行四边形菱形矩形正方形平行四边形菱形 当一个四边形的对角线满足什么条件时,它的中点四边形是平行四边形、矩形、菱形、正方形? 对中点四边形EFGH的形状起主要作用的要素是什么?思 考归纳,使我飞跃不相等
不垂直相等垂直相等且垂直?平行四边形?菱形矩形正方形如图,四边形EFGH是四边形ABCD的中点四边形,那么结论1:结论3:结论2:四边形EFGH是平行四边形结论4:(北京中考题改编)四边形ABCD中,AC=6,BD=8,AC⊥BD,顺次连结四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连结四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
(1)求证:四边形A1B1C1D2是矩形;
(2)写出四边形A1B1C1D1的面积;
(3)写出四边形A2B2C2D2的周长;
(4)写出四边形AnBnCnDn的面积; 小 结本节课我复习了
本节课我探究了
本节课给我的启发是下课前巩固题:下列叙述哪几个是正确的?(1)平行四边形的对角线相等;
(2)矩形的四个角都相等;
(3)菱形的对角线互相垂直平分;
(4)有一个角是直角且邻边相等的平行四边形是正方形;
(5)一组对边平行的四边形是梯形;
(6)有两个角相等的梯形是等腰梯形;
(7)对角线相等的四边形是矩形;
(8)在梯形中上面的底叫做上底,下面的底叫做下底;
(9)一组对边平行且相等的四边形是平行四边形。
整理与探究一、四边形与特殊四边形的关系四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边
分别平行有一个角
是直角邻边相等邻边相等有一个角
是直角 一组对边平行另
一组对边不平行两腰相等 有一个角
是直角有一个角是直角且邻边相等二、几种特殊四边形的常用判定方法 平行
四边形(1)两组对边分别平行(2)一组对边平行且相等(3)两组
对边分别相等 (4)两组对角分别相等(5)对角线互相平分矩 形(1)有三个角是直角;(2)有一个角是直角的平行四边形;(3)两条对角线相等且平分的四边形。 菱 形(1)四条边都相等;(2)有一组邻边相等的平行四边形;(3)两条对角线互相垂直平分。正方形(1)有一组邻边相等的矩形;(2)有一个角是直角的菱形。等 腰
梯 形(1)同一条底边上的两个内角相等的梯形;(2)两条对角线相等的梯形。三、几种特殊四边形的性质平行
四边形矩 形菱 形正方形等腰梯形边对边平行
且相等对边平行
且相等对边平行,
四条边都相等对边平行,
四条边
都相等两底平行,
两腰相等角对角相等四个角
都是直角对角相等四个角
都是直角同一底上的
两个角相等对 角 线两条对角线互相平分两条对角线互相平分且相等两条对角线互相垂直平分,
每条对角线平分一组对角两条对角线互相垂直平分
且相等,每条对角线平分
一组对角两条对角线相等C如图,顺次连结△ABC的各边中点D、E、F分,△DEF 叫做△ABC的中点三角形。2、△DEF∽△CBA3、4、1、DE∥BC,DF∥AC,EF∥ABF中点四边形知识探究( 顺次连结四边形各边中点所组成的四边形称为中点四边形)猜想:顺次连结四边形各边中点所组成的四边形是怎样的图形?已知:在四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD边上的中点.求证:四边形EFGH是平行四边形.结论:任意四边形的中点四边形是平行四边形. 如果我们改变四边形ABCD的形状,那么,对于它的中点四边形,又是怎样的图形呢?探索,我能发现 平行四边形、矩形、菱形、梯形、等腰梯形的中点四边形是怎样的图形?1、探索:平行四边形ABCD的中点四边形EFGH是怎样的图形?ABCHDEFG2、菱形、矩形、正方形的中点四边形3、梯形、等腰梯形的中点四边形求证:等腰梯形的中点四边形是菱形。平行四边形的中点四边形为_____________;
矩形的中点四边形为________;
菱形的中点四边形为________;
正方形的中点四边形为________;
梯形的中点四边形为_____________;
等腰梯形的中点四边形为________。探索,我的发现平行四边形菱形矩形正方形平行四边形菱形 当一个四边形的对角线满足什么条件时,它的中点四边形是平行四边形、矩形、菱形、正方形? 对中点四边形EFGH的形状起主要作用的要素是什么?思 考归纳,使我飞跃不相等
不垂直相等垂直相等且垂直?平行四边形?菱形矩形正方形如图,四边形EFGH是四边形ABCD的中点四边形,那么结论1:结论3:结论2:四边形EFGH是平行四边形结论4:(北京中考题改编)四边形ABCD中,AC=6,BD=8,AC⊥BD,顺次连结四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连结四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
(1)求证:四边形A1B1C1D2是矩形;
(2)写出四边形A1B1C1D1的面积;
(3)写出四边形A2B2C2D2的周长;
(4)写出四边形AnBnCnDn的面积; 小 结本节课我复习了
本节课我探究了
本节课给我的启发是下课前巩固题:下列叙述哪几个是正确的?(1)平行四边形的对角线相等;
(2)矩形的四个角都相等;
(3)菱形的对角线互相垂直平分;
(4)有一个角是直角且邻边相等的平行四边形是正方形;
(5)一组对边平行的四边形是梯形;
(6)有两个角相等的梯形是等腰梯形;
(7)对角线相等的四边形是矩形;
(8)在梯形中上面的底叫做上底,下面的底叫做下底;
(9)一组对边平行且相等的四边形是平行四边形。
